Çukur ayna

Çukur ayna üzerine gelen ışınları belli bir noktada toplayan ayna.

Optik
Işığın doğası
Işık
Işık hızı
Huygens-Fresnel ilkesi
Fermat ilkesi
Optik aygıtlar
Ayna
Mercek
Prizma
Büyüteç
Kamera
Mikroskop
Teleskop
Lazer
Göz
Olaylar
Yansıma
Tam yansıma
Kırılma
Saçılma
Girişim
Kırınım
Polarizasyon

Terimler

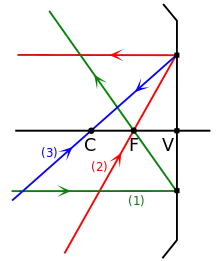
C merkezli, R yarıçaplı bir çemberin herhangi bir yay parçasını çıkartıp dış kısmını sırladığımızda bir çukur ayna elde ederiz. Bu çukur aynada

• C noktası eğrilik merkezi
• R uzunluğu, eğrilik yarıçapı
• F noktası odak (aynı zamanda R uzunluğunun yarısı)
• Çemberin çapı, asal eksen
• Işının aynaya değdiği noktadaki aynaya dik doğru normal olarak tanımlanır.

Işının yansıması

Çukur aynaya gelen ışınlar yansıma kanunlarına uygun olarak yansır. Ancak düzlem aynadan farklı olarak ayna küresel olduğundan normal aynanın her noktasında farklı doğrultudadır. Bu yüzden asal eksene paralel gelen ışınlar tek bir noktada toplanır. Bazı özel noktalardan geçen ışınların yansımasını şöyle tanımlayabiliriz.

1. Asal eksene paralel gelen ışınlar, odak noktasından geçecek şekilde yansır.
2. Odak noktasında geçecek şekilde gelen ışınlar, asal eksene paralel yansır.
3. Merkezden gelen ışınlar, merkez üzerinden yansır.

Çukur aynada özel ışınlar

Görüntü oluşumu

Bir cismin, çukur aynada oluşan görüntüsünün yeri ve boyu aşağıdaki formüllerle hesaplanır.

${\displaystyle m\equiv {\frac {h_{\mathrm {i} }}{h}}=-{\frac {q}{p}}}$

${\displaystyle {\frac {1}{q}}+{\frac {1}{p}}={\frac {1}{f}}}$

• ${\displaystyle m}$: Büyütme
• ${\displaystyle h_{\mathrm {i} }}$: Görüntünün boyu
• ${\displaystyle h}$: Cismin boyu
• ${\displaystyle q}$: Cismin uzaklığı
• ${\displaystyle p}$: Görüntünün uzaklığı
• ${\displaystyle f}$: Odak uzaklığı

Yukarıdaki formüllerde işaret seçimi oldukça önemlidir. Cismin görüntüsünün ters ya da düz olduğu veya aynanın arkasında ya da önünde oluştuğu işarete bağlıdır. İşaret seçiminde aşağıdakilere dikkat edilmelidir.

Cisim ayanın önündeyse	p pozitif
Cisim aynanın arkasındaysa	p negatif
Görüntü aynanın önündeyse (gerçek görüntü)	q pozitif
Görüntü aynanın arkasındaysa (sanal görüntü)	q negatif
Eğrilik merkezi aynanın önündeyse	f ve R pozitif
Eğrilik merkezi aynanın arkasındaysa (Tümsek ayna)	f ve R negatif
M pozitifse	görüntü düz
M negatifse	görüntü ters

Yukarıdaki formüller yorumlanarak bazı özel noktalardaki cisimlerin görüntüleri hesaplanabilir.

• 
• 
• 
• 

Kullanım alanları

• Dişçi aynasında görüntüyü büyütmek için,
• Güneş fırınında yüksek sıcaklıklar elde etmek için,
• Teleskopta ışığı yansıtmak için,
• El feneri, mikroskop ve araba farında ışığı belli bir bölgeye odaklamak için kullanılır.