Anahtar Çizelgesi

Kriptografide ürün şifreleri, verilerin (de)şifrelenmesinin genelde çevrimlerin iterasyonu ile yapıldığı belirli türdeki şifrelemelerdir. Çevrim sabiti olarak adlandırılan çevrime özgü sabit değerler ve çevrim anahtarı olarak adlandırılan şifre anahtarından türetilmiş çevrime özgü veriler haricinde her bir çevrim için kurgu genellikle aynıdır. Anahtar çizelgesi (key schedule), tüm çevrim anahtarlarını anahtardan hesaplayan bir algoritmadır.

DES'in anahtar çizelgesi

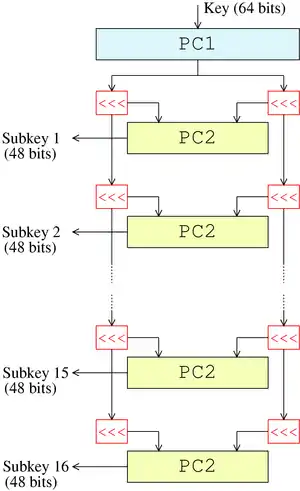
Anahtar çizelgesinin bazı türleri

• Bazı şifrelemelerin basit anahtar çizelgeleri vardır. Örneğin, TEA blok şifreleme algoritması 128 bitlik anahtarı 32 bitlik dört parçaya böler ve bunları ardışık çevrimlerde tekrar tekrar kullanır.
• DES, 56 bitlik anahtarın 28 bitlik iki parçaya bölündüğü, sonrasında ise her iki parçanın ayrı ayrı işleme sokulduğu bir anahtar çizelgesine sahiptir. Ardışık çevrimlerde her bir parça bir ya da iki bit (her çevrim için belirtilen değerde) sola döndürülür ve daha sonra 48 çevrim anahtar biti, sol yarıdan 24 bit ve sağ yarıdan 24 bit olacak şekilde “Permuted Choice 2 (PC-2)” kullanılarak seçilir. Rotasyonlar; her bir çevrim anahtarında farklı bir bit kümesinin kullanılması yönünde bir etkiye sahiptirler (her bit 16 çevrim anahtarının yaklaşık 14ünde kullanılır).
• İlişkili anahtar saldırıları ve geçişli saldırılar gibi kripto analiz türlerine karşı koyma amacıyla şifreleme anahtarı ile çevrim anahtarları arasındaki basit ilişkilerden kaçınmak için birçok modern şifreleme yöntemi, çekilen çevrim anahtarlarından "genişletilmiş anahtar" oluşturacak daha detaylı anahtar çizelgeleri kullanırlar. Rijndael (AES) ve Blowfish gibi bazı şifreleme yöntemleri, anahtarlarını genişletmek için; bazen birkaç bilerek seçilmiş sayı ile başlatılmış, şifreleme algortimalarının veri yolunda da kullanılan işlemleri kullanırlar. RC5 gibi diğer şifrelemeler, şifreleme fonksiyonlarından kısmen ya da tamamen farklı fonksiyonlarla anahtarları genişletirler.

Notlar

Knudsen ve Mathiassen (2004), anahtar çizelgesinin lineer ve diferansiyel kripto analize karşı dayanıklılık sağlamada rol oynadığını gösteren deneysel kanıtlar sağlamıştır. Küçük (toy) Feistel şifrelemede, karmaşık ve iyi tasarlanmış anahtar çizelgelerinin kötü tasarlanan anahtar çizelgelerine kıyasla, diferansiyellerin ve lineer gövdelerin olasılıkları için düzgün bir dağılıma daha hızlı ulaşabildiği gözlemlenmiştir.

Kaynakça

• Lars R. Knudsen and John Erik Mathiassen, On the Role of Key Schedules in Attacks on Iterated Ciphers, ESORICS 2004, pp322–334.
• Uri Blumenthal and Steven M. Bellovin, A Better Key Schedule for DES-like Ciphers10 Ağustos 2017 tarihinde Wayback Machine sitesinde arşivlendi., Proceedings of PRAGOCRYPT '96.