Basit makine

Basit makineler: insanların, işlerini kolaylaştırmak için geliştirildiği araçlardır. Basit makineler, kuvvetten kazanç sağlamak, yoldan kazanç sağlamak, kuvvetin yönünü değiştirmek, işin yapılma hızını değiştirmek ya da bir enerji türünü başka bir enerji türüne dönüştürmek amaçlarıyla kullanılabilir.

Bir tür kaldıraç. Bu kaldıraçta kuvvet kolu ve yük kolu eşittir.

Tarihçe

Basit bir makine fikri, M.Ö. 3. yüzyıl civarında Yunan filozofu Arşimed'le ortaya çıktı: Koldaki mekanik avantaj prensibini keşfetti. Arşimet'in kolu ile ilgili ünlü lafı: "Bana durmak için bir yer ver, ben de Dünyayı hareket ettireceğim." ,mekanik avantaj kullanılarak elde edilebilecek kuvvet yükseltme miktarında bir sınır olmadığı iddiasını ifade eder. Daha sonra Yunan filozofları klasik beş basit makineyi (eğik düzlem hariç) tanımladılar ve (ideal) mekanik avantajlarını hesaplayabildiler. Mesela, İskenderiye Heron (MS. 10–75) çalışmalarında “harekete geçen bir yük” ayarlayabilen beş mekanizma listeler; kolu, ırgat, kasnak, kama ve vida, ve bunların imalat ve kullanımlarını açıklar. Ancak Yunanların anlayışı basit makinelerin statiği (kuvvetler dengesi) ile sınırlıydı ve dinamikleri, kuvvet ile mesafe arasındaki değişimleri ya da iş kavramlarını içermiyordu.

Rönesans döneminde, Mekanik Güçlerin dinamikleri, basit makinelerin çağrıldığı gibi, sonunda yeni mekanik kavramına öncülük edecekleri, uygulayabilecekleri güçlerin yanı sıra, bir yükü ne kadar kaldırabilecekleri açısından incelenmeye başlandı. iş. 1586'da Flaman mühendis Simon Stevin, eğik düzlemin mekanik avantajını elde etti ve diğer basit makinelere dahil edildi. Basit makinelerin tam dinamik teorisi, İtalyan bilim adamı Galileo Galilei tarafından 1600 yılında Le Meccaniche'de çalışarak makinelerin altında yatan kuvvetli kuvvetlendirici olarak benzerliğini gösterdi. Basit makinelerin enerji yaratmadığını, sadece dönüştürdüğünü açıklayan ilk kişi oydu.

Makinelerde klasik kayar sürtünme kuralları Leonardo da Vinci (1452–1519) tarafından keşfedilmiştir, ancak yayınlanmamıştır ve yalnızca defterlerinde belgelenmiştir ve sürtünmenin eterik bir sıvı olduğuna inanmak gibi Newton öncesi bilime dayanmaktadır. Guillaume Amontons (1699) tarafından yeniden keşfedilmiş ve Charles-Augustin de Coulomb (1785) tarafından daha da geliştirilmiştir.

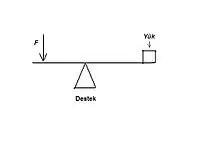
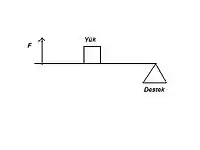
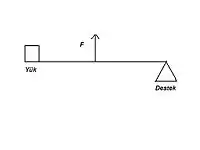
Kaldıraçlar

Bu tür kaldıraçlarda, formül; "Kuvvet x Kuvvet kolu = Yük x Yük kolu"dur.

Kuvvet kolu, kuvvet ile destek arasındaki mesafedir. Yük kolu da, yük ile destek arasındaki mesafedir.

Bu kaldıraçta kuvvet kolu, yük kolundan uzundur. O yüzden, yükü kaldırmak için daha az kuvvet uygulanmalıdır.

Bu kaldıraçta kuvvet kolu, yük kolundan kısadır. O yüzden, yükü kaldırmak için daha fazla kuvvet uygulanmalıdır.

Kullanımları

Kaldıraçlar az kuvvet ile büyük yükleri kaldırmak için kullanılır. Yük kolu ile kuvvet kolu uzunlukları eşitse, uygulanan kuvvet yük kadar olur. Kuvvet kolu ne kadar büyükse, yükü kaldırmak için harcanacak kuvvet o kadar az olur.

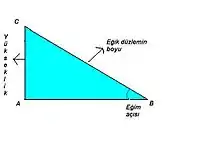
Eğik düzlem

Bir yükü, ağırlığından daha küçük kuvvetle yukarıya kaldırmak amacıyla kullanılır.

Eğik düzlem resminde, A noktasındaki cismi C noktasına çıkarmak için yapılan iş, aynı cismi B noktasından C noktasına çıkarmak için yapılan işe eştir. Buna göre:

W_AC = W_BC denilebilir.

Az bir kuvvetle yükü C noktasına çıkarmak için;

• Eğik düzlem boyu uzatılabilir.
• Eğim açısı küçültülebilir.

Eğim açısı büyürse/eğik düzlemin boyu kısalırsa, daha çok kuvvet gerekir.

Eğik düzlem ve gösterilişi.

Sabit Makara

Hareketli Makara

Palanga

Makaralar

İş yapma kolaylığı sağlayan basit makinelerden biri makaradır. 3 çeşit makara vardır:

• Sabit makaralar
• Hareketli makaralar
• Palangalar

Sabit makara

Sabit makaralarda yalnız makara döner. Bir yere monte edilmiş şekilde kullanılan makaralardır. Kullanımda kuvvetin yönünü değiştirme özelliği vardır. Bu makaralar kuvvetten kazanç sağlamazlar. Yükü kaldırmak için yüke eşit bir kuvvet kullanılır. 50 N yükü kaldırmak için ipin ucunu 50 N kadar çekmek gerekir.

Hareketli makara

Hareketli makaralarda yük, serbest olan makaraya bağlanır. Formül, "Kuvvet = Yük/makara sayısı" dır.

Palanga

Palanga, az kuvvetle çok yük kaldırmak için kullanılan makaralar kombinasyonudur. Sabit makaraya, aynı gövdeye bağlı bir veya daha fazla hareketli makaranın ilâve edilmesiyle meydana gelir.

Bu sistemlerde kuvvet bölünerek yükün bir kısmının sabit makaralara taşıtılmasıyla uygulanacak kuvvet azaltılabilir. Palangalarda yükü kaldıracak kuvvet, yükün ağırlığının makara sayısına bölümü ile hesaplanır. Palangalarda kuvvet kazancı hareketli makaralara etki eden ip sayısına eşittir. Palangalarda uygulanacak kuvvet hesaplanırken hareketli makaraların ağırlıkları da hesaba katılır. Palangalarda kuvvetten kazanç vardır.