Brianchon teoremi

Geometride Brianchon teoremi, bir konik kesit etrafındaki bir altıgen ile sınırlandırıldığında, ana köşegenlerinin (karşıt köşeleri birleştirenler) tek bir noktada kesiştiğini belirten bir teoremdir. Adını Fransız matematikçi Charles Julien Brianchon'dan (1783–1864) almıştır.

Brianchon teoremi

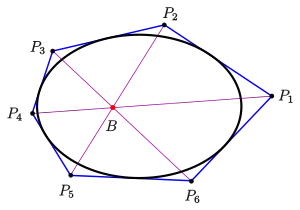
Biçimsel açıklama

${\displaystyle P_{1}P_{2}P_{3}P_{4}P_{5}P_{6}}$, bir konik kesitin altı teğet çizgisinden oluşan bir altıgen olsun. Ardından ${\displaystyle {\overline {P_{1}P_{4}}},\;{\overline {P_{2}P_{5}}},\;{\overline {P_{3}P_{6}}}}$ çizgileri (her biri zıt köşeleri birbirine bağlayan uzatılmış köşegenler), Brianchon noktası olan tek bir ${\displaystyle B}$ noktasında kesişir.^{:p. 218}[1]

Pascal teoremi ile bağlantı

Bu teoremin kutupsal karşılıklı ve izdüşümsel çifti, Pascal teoremini verir.

Dejenerasyonlar

Brianchon teoreminin 3 teğet dejenerasyonu

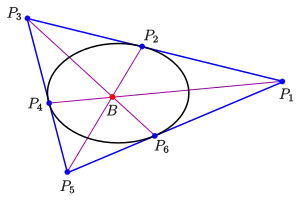
Pascal teoremine gelince, Brianchon teoremi için de dejenerasyonlar vardır: İki komşu teğeti çakıştıralım. Kesişme noktaları bir konik noktası haline gelir. Şekilde üç çift komşu teğet çakışmaktadır. Bu prosedür, üçgenlerin iç elipsleri hakkında bir açıklama ile sonuçlanır . İzdüşümsel bir bakış açısından iki üçgen ${\displaystyle P_{1}P_{3}P_{5}}$ ve ${\displaystyle P_{2}P_{4}P_{6}}$, ${\displaystyle B}$ merkezi ile perspektif olarak uzanmaktadır. Bu, birini diğer üçgene eşleyen merkezi bir doğrudaşlama (kolineasyon) olduğu anlamına gelir. Ancak sadece özel durumlarda bu doğrudaşlama afin bir ölçeklendirmedir. Örneğin, Brianchon noktasının ağırlık merkezi olduğu bir Steiner iç elipsi için.

Afin düzleminde

Brianchon teoremi hem afin düzleminde hem de gerçek izdüşümsel düzlemde doğrudur. Bununla birlikte, afin düzlemindeki ifadesi bir bakıma izdüşümsel düzlemdekinden daha az bilgilendirici ve daha karmaşıktır. Örneğin, bir parabole beş teğet doğru düşünün. Bunlar, altıncı tarafı sonsuzdaki çizgi olan bir altıgenin kenarları olarak düşünülebilir, ancak afin düzleminde sonsuzda bir çizgi yoktur. İki durumda, (var olmayan) bir tepe noktasından karşı tepe noktasına doğru bir çizgi, beş teğet çizgiden birine paralel bir çizgi olacaktır. Brianchon'un teoremi yalnızca afin düzlemi için ifade edildiğinden, böyle bir durumda farklı şekilde ifade edilmesi gerekirdi.

Brianchon teoreminin izdüşümsel çifti, afin düzleminde istisnalara sahiptir, ancak izdüşümsel düzlemde değildir.

İspat

Brianchon'un teoremi, radikal eksen veya karşılıklılık fikriyle kanıtlanabilir.

İlave okumalar

• John B Mertie, (1948), Application Of Brianchon's Theorem to Construction of Geologic Profiles. GSA Bulletin, 59 (8): ss. 767–786. doi:10.1130/0016-7606(1948)59[767:AOBTTC]2.0.CO;2, Link
• James, G. (1930). Generalizations of Pascal's and Brianchon's Theorems. The American Mathematical Monthly, 37(2), ss. 78-80.
• Ogura, K. (1913). Some theorems in the geometry of oriented circles in a plane. Tohoku Mathematical Journal, First Series, 3, ss. 104-109.
• Smart, R. (1942). 1626. Brianchon's Theorem. The Mathematical Gazette, 26(271), s. 190.
• Brown, A. (2003). 87.81 A connection between Brianchon's theorem and the seven circles theorem. The Mathematical Gazette, 87(510), ss. 569-572.
• Langley, E. M. (1912). 379. Pascal’s Theorem; Brianchon’s Theorem; Cross-Centre and Cross-Axis. The Mathematical Gazette, 6(100), ss. 375-378.
• Smart, R. (1942). 1600. Analytical Proof of Brianchon's Theorem. The Mathematical Gazette, 26(270), s. 137.
• Ota, T. (1921). Pascal-Brianchon Theorems for Higher Curves and Surfaces. Tohoku Mathematical Journal, First Series, 19, ss. 69-88.
• Odani, K., & Takase, S. (1999). 83.51 On a theorem of Brianchon and Poncelet. The Mathematical Gazette, 83(498), ss. 483-486.
• Russell, J. W. (1893). Chapter XV: Pascal's theorem and Brianchon's theorem. In An elementary treatise on pure geometry with numerous examples (ss. 156-162). Cornell University Library.
• Fenwick, S. (1843). XXV. Investigation of Brianchon's theorem. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 22(144), ss. 167-168.
• Tan, K., & Thébault, V. (1962). Some proofs of a theorem on quadrilateral. Mathematics Magazine, 35(5), ss. 289-294.
• Robert Bix, (2006), Conics and Cubics: A Concrete Introduction to Algebraic Curves, s. 117, Springer-Verlag New York, doi:10.1007/0-387-39273-4, 978-0-387-39273-8

Dış bağlantılar

• Wolfram MathWorld - Brianchon's Theorem
• cut-the-knot - Brianchon's Theorem
• ProofWiki - Brianchon's Theorem
• Proof of Brianchon's Theorem
• Brianchon's Theorem

Ayrıca bakınız

• Yedi çember teoremi
• Pascal teoremi

Kaynakça

1. Projective Geometry. 2nd. Springer-Verlag. 1987. Theorem 9.15, s. 83. ISBN 0-387-96532-7.