Dinostratus teoremi

Geometride, Dinostratus teoremi, eğer trisektris düz kenar bir cetvel ve pergele ek olarak kullanılabilirse, daireyi kareyle çevrelemeye izin veren Hippias trisektrisinin bir özelliğini tanımlar. Teorem, ismini, MÖ 350 civarında daireyi kareyle çevreleme çalışırken kanıtlayan Yunan matematikçi Dinostratus'tan almıştır.

{\frac {|AE|}{|AB|}}={\frac {2}{\pi }}

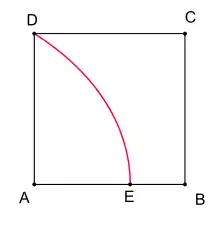
Teorem, Hippias trisektrisinin, ilişkili karesinin kenarlarından birini $2:\pi$ oranıyla böldüğünü belirtir.

Hippias trisektriksindeki keyfi noktalar yalnızca çember ve pergel ile oluşturulamaz, ancak yoğun bir alt küme ile oluşturulabilir. Özellikle, trisektrisin karenin kenarıyla buluştuğu noktayı tam olarak çizmek mümkün değildir. Bu nedenle Dinostratus'un yaklaşımı, çemberin kareyle çevrelenmesi klasik probleminin "gerçek" çözümü olarak görülmez.

Kaynakça

Thomas Little Heath: A History of Greek Mathematics. Volume 1. From Thales to Euclid. Clarendon Press 1921 (Nachdruck Elibron Classics 2006), ss. 225–230 (Google Kitaplar'da online copy, s. 225,)
Horst Hischer: Klassische Probleme der Antike - Beispiele zur "Historischen Verankerung". İçinde: Blankenagel, Jürgen & Spiegel, Wolfgang (Hrsg.): Mathematikdidaktik aus Begeisterung für die Mathematik - Harald Scheid für Festschrift. Stuttgart/Düsseldorf/Leipzig: Klett 2000, S. 97–118 (Almanca).
Carl B. Boyer & Uta C. Merzbach, (2010), A History of Mathematics, (3. bas), ss. 87-88, 978-0470525487, (İlk basım: 1968)
https://mathshistory.st-andrews.ac.uk/Biographies/Dinostratus/

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.