Elektronik bant yapısı

Katı hal fiziğinde, bir katının elektron kuşak yapısı (ya da sadece kuşak yapısı); katıdaki bir elektronun sahip olabileceği enerji aralıkları (enerji bandı, izinli bant, ya da sadece bant olarak adlandırılır), ya da sahip olamayacağı enerji aralıkları olarak tanımlanır. Enerji bant teorisi bu bant ve bant boşluklarını atom veya moleküllerin büyük periyodik kafeslerindeki bir elektron için, izinli kuantum mekaniksel dalga fonksiyonlarını inceleyerek çıkarır. Bant teorisi katıların birçok fiziksel özelliklerini; örneğin elektriksel direnç ve optik soğurum gibi, açıklamak için başarılı bir biçimde kullanılmaktadır ve katıhal cihazları (transistörler, güneş pilleri vb.) anlamanın temelini oluşturmaktadır.

Neden bant ve bant aralıkları ortaya çıkar?

Tek, izole edilmiş atomun elektronları atomik orbitalleri doldurur. Her orbital ayrı enerji seviyeleri oluşturur. Birden çok atomun bir araya gelmesiyle molekül oluşur, ve atomların atomik orbitalleri de birleşerek her birinin ayrı enerji seviyeleri oluşturduğu, moleküler orbitali oluşturur. Birleşen atom sayısı arttıkça, moleküler orbitaller daha da genişler, ve moleküldeki enerji seviyeleri gittikçe artan bir yoğunluğa ulaşır. En sonunda atomların toplamından çok devasa bir molekül oluşur, ya da başka bir deyişle, bir katı. Bu devasa molekül için enerji seviyeler birbirine o kadar yakındır ki bir bütün oluşturuyorlar gibi düşünülebilir.

Bant boşlukları temelde, enerji bantlarının sonu olan genişliklerinin bir sonucu olarak, hiçbir bant tarafından kaplanmamış artık enerji aralıklarıdır. Bantların farklı genişlikleri vardır ve bu genişlikler atomik orbitallerin örtüşme derecesine bağlıdır. İki komşu bant enerji aralığını tamamen kaplayacak genişlikte olmayabilir. Örneğin çekirdek orbitalleri(1s elektronları gibi) ile ilişkili bantlar, komşu atomların örtüşmesinin çok küçük olması sebebiyle, çok dardırlar. Sonuç olarak çekirdek bantları arasında büyük bant aralıkları olmaya eğilimi vardır. Daha çok örtüşme yapan daha geniş orbitalli büyük bantlar, yüksek enerjide gittikçe daha da genişlerler ve bant boşluğu kalmaz.

Temel kavramlar

Bant yapısı teorisi'nin varsayımları ve limitleri

Başlangıç için teorinin daha basitleştirilmesi adına bazı önemli bilgiler verilebilir:

1. Sınırsız boyut sistemi: Bantları sürekli olabilmesi için çok büyük parça materyali dikkate almalıyız. Bant yapısı kavramı sadece indirgenmiş boyutlarda “büyük” olarak alınlarak genişletilebilir, iki boyutlu elektron sistemlerindeki gibi.

2. Homojen sistem: Yapısal özellik olarak bant yapısı kavramı, bir maddenin bir şekilde homojen olduğu varsayar. Pratikte bunun anlamı, bant yapısının düzenli yapıdaki bir maddenin içindeki bir kitle olmasıdır.

3. Etkileşimsizlik: Bant yapısı “tek-elektron hali”ni tarif eder. Bu hallerin varlığı elektronların diğer elektronlar, fotonlar ve örgü titreşimleri ile dinamik bir etkileşime geçmeden, statik potansiyelde yolculuk yaptığını kabul eder.

Yukarıdaki varsayımlar birçok önemli pratiksel durumlarla çürütülmüştür. Bant yapısının kullanımını anlamak için bant teorisinin limitlerine de bakılmalıdır:

• Homojen olmama ve arayüzler: Yüzeylerin, bağlantı noktalarının ve diğer homojensizliklerin yanında, bant yapısı gövdesi bozulur. Sadece lokal, küçük ölçekli bozulmalar (örn. Bant boşluğunun içindeki yüzey halleri veya katkı maddesi halleri) değil, aynı zamanda lokal yük dengesizlikleri de görülür. Bu yük dengesizliklerinin elektrostatik etkileri yarıiletkenlere, yalıtkanlara ve vakuma kadar uzanır.
• Aynı çizgide, çoğu elektronik etkiler (kapasitans, elektrik iletkenliği, elektrik alan perdeleme), yüzey ve/veya arayüz yakınlarından elektron geçişi fiziğini kapsar. Bu etkilerin tam tanımları, bant yapısı resminde, en azından elektron-elektron etkileşimlerinin tam olgunlaşmamış modelini gerektririr.
• Küçük sistemler: Her boyutta küçük olan sistemler için (örn. Küçük molekül veya kuantum noktası), sürekli bant yapısı yoktur. Küçük ve büyük boyutlar arası geçiş, mezoskopik fiziğin konusudur.
• Güçlü bağlantılı maddeler: Bazı maddeler (süperiletkenler, Mott yalıtkanları ve dahası) tek-elektron hali ile anlaşılamaz. Bu maddelerin elektronik bant yapıları yetersizce (ya da en azından detaylıca olmayan) açıklanmış ve fizikleri ile ilgili bilgi sağlanmamıştır.

Kristal simetrisi ve dalga vektörleri

Özel simetri noktaları için işaretleri gösteren yüzey merkezli kübik kafesin Brillouin bölgesi.

Sıkı bağlanma modeli ile oluşturulan silikon (Si), germanyum (Ge), galyum arsenit (GaAs), ve indiyum arsenit (InAs) için kuşak yapı grafiği. GaAs ve InAs direkt olarak kuşak boşluk materyali iken Si ve Ge dolaylı yoldan olanlardır.

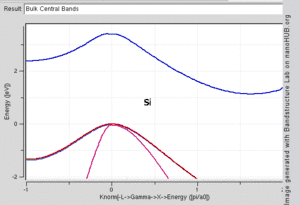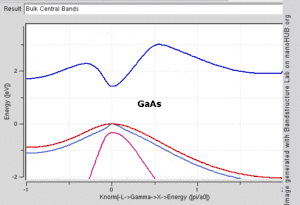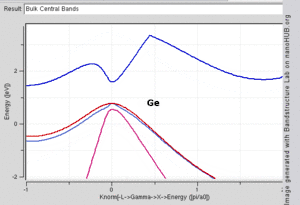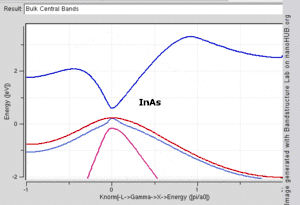
Bant yapısı hesaplamaları, kristal örgüsünün simetrisini kullanarak, periyodik doğasından yararlanır.

${\displaystyle \psi _{n\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n\mathbf {k} }(\mathbf {r} )}$,

“k” dalga vektörü olarak adlandırılır. k’nın her değeri için, Schrödinger denkleminin n, the band index, ile gösterilen birden çok çözümü vardır, ve n değeri basitçe enerji bantlarını gösterir. k değiştikçe her bir enerji seviyesi yavaşça değişir ve a smooth band of states oluşturur. Her bant için o banttaki elektronların dağılma ilişkisini En(k) fonksiyonu ile tanımlayabiliriz.

Dalga vektörü Brillouin alanının, kristalin kafesiyle alakalı çokyüzlü dalga vektörü boşluğu, içindekiherhangi bir değeri alabilir. Brillouin alanının dışında kalanlar, basitçe bu alanın içinde bulunan hallerle fiziksel olarak aynıdır. Brillouin alanındaki özel yüksek simetri noktaları Γ, Δ, Λ, Σ sembolleriyle gösterilir.

Bant’ın şeklini dalga vektörü fonksiyonu olarak gözde canlandırmak zordur çünkü 4 boyutlu uzay, E ‘ye kx, ky, kz, olarak çizmek gerekir. Bilimsel yayınlarda genelde bant yapısı grafikleri En(k) ve k değerlerini birleştiren simetri noktalarından oluşan bir çizgi olarak gösterilir. Bant yapısını görselleştirmek için diğer bir metot ise dalga vektörü uzayında sabit enerjili izoyüzey olarak koyarak, enerji belli bir değerdeyken tüm halleri gösteren bir grafik çizmektir. Hallerin izoyüzeyi Fermi seviyesindeki enerjiye eşittir ve bu izoyüzey Fermi yüzeyi olarak adlandırılır.

Enerji bant aralıkları, onları çevreleyen hallerin dalga vektörleri kullanılarak sınıflandırılır:

• Doğrudan bant aralığı: bant aralığının üstündeki en düşük enerjili halin, aşağısındaki en yüksek enerjili hale aynı k değerine sahip olması
• Dolaylı bant aralığı: farklı k değerlerine sahip olan birbirlerine en yakın, bant aralığının üstündeki ve altındaki haller.

Asimetri: kristal yapıda olmayan katılarda bant yapıları

Genelde elektronik bant yapıları kristal yapıdaki maddelerle özdeşleştirilse de, yarı kristal ve amorf katılar da bant yapısı gösterebilir. Fakat bu yapılarda kristalin basit simetri yapısı eksik olduğundan ve genelde kesin bir dağılma ilişkisine karar vermek mümkün olmadğı için, teorik olarak çalışmak daha zordur. Sonuç olarak katıların bant yapısı ile ilgili varolan teorik çalışmaların hemen hemen hepsi kristal maddeler üzerine yoğunlaşır.

Hal yoğunluğu

Hal yoğunluğu fonksiyonu g(E) birim hacme, birim enerjiye, E civarındaki elektron enerjileri için, düşen elektronik hal sayısı olarak tanımlanır.

Hal yoğunluğu fonksiyonu bant teorisine dayalı hesaplamalar için önemlidir. Bu fonksiyon optik soğurum hesaplamaları için hem uyarılabilir elektron sayısını hem de bir elektron için son hal sayısını sağlar. Aynı zamanda elektriksel iletkenlik hesaplamalarında mobile state sayısını ve elektron saçılma hızlarını hesaplarken saçılmadan sonraki son hal sayılarını verir. Bant boşluğu içindeki enerjiler için, g(E) = 0.

Bantları doldurma

Termodinamik dengede E enerji halinin bir elektronla dolma olasılığı Fermi-Dirac dağılımı(Pauli dışlanım ilkesini hesaba alan bir termodinamik dağılım) ile verilir:

${\displaystyle f(E)={\frac {1}{1+e^{{(E-\mu )}/{k_{\rm {B}}T}}}}}$

Formüldeki bileşenler :

• kBT Boltzmann sabiti ve sıcaklığın çarpımı,
• µ elektronların toplam kimyasal potansiyeli veya Fermi seviyeleri ( yarıiletken fizikte bu büyüklük daha çok EF ile gösterilir).

Bir katının Fermi seviyesi o katıya uygulanan ve voltmetreyle ölçülen gerilimle doğrudan ilişkilidir. Genellikle bant yapısı grafiklerinde Fermi seviyesi sıfır alınır(isteğe bağlı/rastgele seçilmiş bir değer).

Maddedeki elektronların yoğunluğu Fermi-Dirac dağılımının hallerin yoğunluğuyla çarpımının integralidir:

${\displaystyle N/V=\int _{-\infty }^{\infty }g(E)f(E)\,dE}$

Sonsuz sayıda bant olmasına ve böylece sonsuz sayıda hal olmasına rağmen, sadece sınırlı sayıda elektron bu bantlara yerleşir. Tercih edilen elektron sayısı elektrostatiğin bir sonucudur: maddenin yüzeyinin yükle yüklenebilmesine rağmen maddenin içindeki kitle nötr yükü tercih eder. Yükün nötr olma durumu N/V değerinin maddedeki proton yoğunluğuyla aynı olmasıdır. Bunun olması için maddenin elektrostatik olarak kendini ayarlaması, Fermi seviyesine göre doğru denge olana kadar bant yapısını enerji içinde aşağı ya da yukarı kaydırması (dolayısıyla g(E)yi kaydırması) gerekir.

Fermi seviyesi yakınındaki bantların isimleri (iletim bandı, değerlik bandı)

Bir katıda, atomların sonsuz enerji seviyesi olması gibi, sonsuz sayıda izinli bant vardır. Ancak, bantların çoğunun çok yüksek enerjisi vardır ve genelde sıradan durumlarda dikkate alınmazlar. Tam aksine çekirdek orbitalleri ile ilişkilendirilen (1s elektronları gibi) çok düşük enerji bantları vardır. Bu düşük enejili çekirdek bantları da her zaman elektronla dolu oldukları ve bu yüzden etkisiz oldukları için genelde dikkate alınmazlar.

En önemli bant ve bant aralıkları—elektronik ve optoelektronikle ilgili olanlar—Fermi seviyesi yakınında olanlardır. Bu bant ve bant aralıklarına maddeye bağlı olarak özel isimler verilmiştir:

• Yarı iletken ya da bant yalıtkanında Fermi seviyesi bant boşluklarıyla çevrilidir, ve “bant boşluğu” olarak adlandırılır. (tırnak işareti bundan önce kullanılan bant boşluğu terimlerinden farklı olduğunu gösterir) .“Bant boşluğu”nun yukarısında ona en yakın olan banta “iletim bandı”, aşağısındaki en yakın banta ise “değerlik bandı” denir. “Değerlik bandı”, çoğu yarıiletkenlerde bu bant değerlik orbitallerinden olduğundan, ve böylece kimya ile paralel olduğu için özellikle böyle adlandırılmıştır.
• Bir metal veya yarımetalde, Fermi seviyesi bir veya daha fazla izinli bantların içinde bulunur. Yarımetallerde bantlar genellikle yarıiletkenlerdeki gibi yük taşımanın daha elektron-gibi mi yoksa boşluk-gibi mi olmasına bağlı olarak “iletken bandı” veya “değerlik bandı” olarak adlandırılır. Fakat yine de değerlik orbitallerinden oluştuğu için çoğunlukla sadece “değerlik bandı” denir. Bir metalin bant yapısındaki bant boşlukları Fermi seviyesine çok uzak olduğundan düşük enerji fiziği için önemsizdir.

Kristallerdeki bant yapısı teorisi

“Ansatz” periyodik kristal örgüdeki elektron dalgalarını, Bloch dalgalarını genellikle ışığın kırılmasının dinamik teorisi ile işlenerek kullanılmasıyla çözüldüğü bir özel durumdur. Her kristal, Bravais örgüsü ile karakterize edilebilen periyodik bir yapıdır, ve her Bravais örgüsü için üç ters örgü vektörü (b1,b2,b3) içeren bir set ile periyodikliği kapsayan bir ters örgüye karar verilebilir. Şimdi, doğrudan örgü ile aynı periyodikliği paylaşan herhangi bir periyodik potansiyel V(r), sadece sıfır olmayan bileşenlerinin ters örgü vektörleri ile ilişkilendirildiği Fourier serisine genişletilebilir:

${\displaystyle V(\mathbf {r} )=\sum _{\mathbf {K} }{V_{\mathbf {K} }e^{i\mathbf {K} \cdot \mathbf {r} }}}$

 K = m1b1 + m2b2 + m3b3 herhangi tam sayıdan oluşan (m1,m2,m3) seti için.

Bu teoriden yola çıkılarak belirli bir maddenin bant yapısını tahmin etmeye yönelik girişim yapılabilir, ancak elektronik yapı hesaplamaları için başlangıçtan beri olan çoğu metotlar, gözlenmiş bant boşuluğunu tahmin etmede başarısızdır.

Kısmen serbest elektron yaklaşımı

Bu yaklaşımda elektronlar arası etkileşimler tamamen yok sayılmıştır. Aynı zamanda bu yaklaşımda Bloch teoremi kullanılmasına izin verilmiştir. Bu da periyodik potansiyelde olan elektronların dalga fonksiyonları ve dalga fonksiyonlarında komşu ters örgü vektörleri arasında sabit faz değişimine kadar periyodik olan enerjileri olduğunu gösterir. Periyodikliğin sonuçları matematiksel olarak aşağıdaki Bloch dalga fonksiyonunda gösterilmiştir:

${\displaystyle {\Psi }_{n,\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n}(\mathbf {r} )}$

${\displaystyle u_{n}(\mathbf {r} )}$ kristal ögü üstünde periyodiktir, yani,

${\displaystyle u_{n}(\mathbf {r} )=u_{n}(\mathbf {r-R} )}$.

Burada n göstergesi n’inci enerji bandını gösterirken, k dalga fonksiyonu elektronun hareket yönüyle, r kristaldeki pozisyon, R ise atom yeri ile alakalıdır.

Bu model metaller gibi komşu atomları küçük olan maddelerde çok daha iyi işler. Bu tip maddelerde atomik orbitallerin örtüşmesi ve komşu atomlardaki potansiyel göreceli olarak büyüktür. Bu durumda elektronun dalga fonksiyonuna (modifiye edilmiş) düzlemsel dalga ile yaklaşılabilir. Aluminyum gibi metallerin bant yapısı boş örgü yaklaşımına daha yakındır.

Sıkı bağlanma modeli

Kısmen serbest elektron yaklaşımına tamamen ters olarak, kristaldeki elektronların bileşen atomların toplanması gibi davranmasıdır. Bu sıkı bağlanma modeki zamana bağlı tek elekton Schrödinger dekleminin ,çözümüne atomik orbitallerin [5] lineer kombinasyonu ile yaklaşılabileceğini varsayar.

${\displaystyle \Psi (\mathbf {r} )=\sum _{n,\mathbf {R} }b_{n,\mathbf {R} }\psi _{n}(\mathbf {r-R} )}$,

katsayıları çözüme en iyi yaklaşımı vermek için seçilmiştir. n atomik enerji seviyesini ve R atom yeri’ni ifade eder. Daha doğru bir yaklaşım, bu fikrin Wannier fonksiyonuna uygulanmasıyla yapılır:

${\displaystyle a_{n}(\mathbf {r-R} )={\frac {V_{C}}{(2\pi )^{3}}}\int _{BZ}d\mathbf {k} e^{-i\mathbf {k} \cdot (\mathbf {R-r} )}u_{n\mathbf {k} }}$;

${\displaystyle u_{n\mathbf {k} }}$ Bloch dagasının periyodik kısmı ve integral Brillouin alanı üzerindedir. Burada n kristaldeki n’inci enerji bantını gösterir. Wannier fonksiyonları atomik orbitallerdeki gibi, atom yerinin yanında yer alır, fakat Bloch fonksiyonlarıyla tanımlandığında kristal potansiyele dayalı çözümlerle daha kesin iişkilendirilirler. Farklı atom yerlerindeki R Wannier fonksiyonları ortogonaldir. Wannier fonksiyonları n’inci enerji seviyesi için Schrödinger çözümü oluşturmada kullanılabilir:

${\displaystyle \Psi _{n,\mathbf {k} }(\mathbf {r} )=\sum _{\mathbf {R} }e^{-i\mathbf {k} \cdot (\mathbf {R-r} )}a_{n}(\mathbf {r-R} )}$.

Bu model atomik orbitallerle kaomşu aromlar arasında sınırlı örtüşme olan maddelerde iyi işler. Örneğin Si, GaAs, SiO2 ve elmas gibi maddelerdeki bant yapıları sp3 orbitallerine dayandırılan sıkı bağlanma Hamiltonian’ı ile çok iyi bir biçimde tanımlanabilir. Geçiş metallerinde karışık Sıkı Bağlanma(SB)- Kısmen Serbest Elektron(KSE) modelleri daha geniş KSE iletim bantları ve daha dar gömülü SB d-bantlarını tamınlamada kullanılır. Wannier fonksiyonlarının atomik orbital kısmının radyal fonksiyonları psödopotansiyel metotlarla kolayca hesaplanır. KSE, SB veya birleşimi KSE-SB bant yapıları hesaplamaları ve bazen psödopotansiyel metotlara dayalı dalga fonksiyonlarına genişletilmiş halleri, sıklıkla daha ileri hesaplamaların ekonomik başlangıç noktası olarak kullanılır.

KKR modeli

Bu yaklaşımın en basit formu örtüşmeyen kürelerin atomik pozisyonda toplanmasıdır(kek kalıbı olarak anılır). Bu bölgelerin içinde bir elektron tarafından deneyimlenen potansiyel, çekirdeğe göre küresel simetriye yakındır. Kalan ara bölgedeki görülen potansiyel yaklaşık olarak sabittir. Potansiyelin atom-merkezli küre ve ara bölge arasında sürekli olmasına zorlanır.

Korringa, Kohn ve Rostocker tarafından değişken uygulamalar önerilmiştir, ve sıklıkla bunşar KKR model olarak adlandırılır.

Yoğunluk-fonksiyonel teorisi

En son fizik literatüründe, elektronik yapıların ve bant grafiklerinin büyük çoğunluğu yoğunluk-fonksiyonel teorisi (YFT)-model değil teori olarak adlandırılır- kullanılarak hesaplanır. YFT-hesaplamalı bantlar birçok durumda deneysel olarak ölçülmüş, örneğin açı-çözümlenmeli ışılyayım spektroskopisi(ARPES) ile, bantlarla uygunluk sağlar. Özellikle bantın şekli YFT ile genel olarak çok iyi üretilir. Ama aynı zamanda YFT bantlarında deney sonuçlarıyla karşılaştırıldığında sistematik hatalar vardır. YFT özellikle yalıtkan ve yarı iletkenlerdeki bant boşluklarını yaklaşık 30-40% kadar daha az tahmin eder.

Genel olarak YFT’nin sadece temel hal özelliklerini (örn. toplam enerji, atomik yapı vb.) tahmin eden bir teori olduğuna, ve uyarılmış hal özelliklerine bu teori belirlenemeyeceğine inanılır. Bu bir kavram yanılgısıdır. Bu Hohenburg-Kohn teoreminin temelidir. Ancak pratikte bir maddedeki temel halde uyarılmış hale geçen elektronların enerjilerini haritalayan bilinen bir işlevsel yoktur. Böylece, literatürde YFT bant grafiği olarak geçen aslında YFT Kohn-Sham enerjilerinin temsilidir (yani; hiç fiziksel yorumlaması olmayan, hayali etkileşimsiz bir sistemin enerjileri, Kohn-Sham sistemi). Kohn-Sham elektronik yapısı gerçekle, bir sistemin yalancı parçacıklı elektronik yapısı ile karıştırılmamalıdır.

Dolayısıyla, prensipte, YFT’ye dayalı Kohn-Sham bir bant teorisi değildir, yani bant grafikleri ve bantların hesaplanması için uygun bir teori değildir. Pratikte genelde zor olsa da, temelde zamana bağlı YFT gerçek bant yapısını hesaplamada kullanılabilir. Ünlü bir yaklaşım ise Hartree-Fock exact exchange’in bir kısmını içeren hibrit fonksiyonlarının kullanılmasıdır; bu, yarıiletkenlerde tahmin edilen bant boşluklarının önemli ölçüde gelişmesidir, fakat metallerde ve bant aralığı geniş maddelerde daha az güvenilir sonuçlar verir.

Green’in fonksiyon metotları ve ab inito GW yaklaşımı

Elektron- elektron etkileşimi çok kütleli etkisini içeren bantları hesaplamak için Green’in fonksiyon metodu denilen yola başvurulabilir. Hatta bir sistemin Green fonksiyonunu bilmek, sistemin hem temel (toplam enerji) hem de uyarılmış halinin gözlenebilmesini sağlar. Green foksiyonunun kutupları, katıların bantı, yalancı parçacık enerjileridir. Green fonksiyonu, sistemin kendi enejisi biliniyorsa Dyson denklemini çözerek hesaplanabilir. Katılar gibi gerçek sistemler için, kendi enejileri çok kompleks bir miktardır ve genellikle problemi çözmek için varsayımlara ihtiyaç vardır. Bu varsayımlardan biri GW yaklaşımıdır, öz enerjiyi Σ = GW matematiksel formunda alır; G Green fonksiyonu, W ise dinamik olarak gösterilen etkileşimdir. Bu yaklaşım bant grafikleri hesaplamasını (ve ayrıca spektral fonksiyonlar gibi ötesinde miktarlar) ele aldığında daha geçeri hale gelir ve aynı zamanda ab inito yolu ile tamamen formülize edilebilir. GW yaklaşımı yalıtkanların ve yarı iletkenlerin bant boşluklarını deneylerle uygun olarak sağlar ve böylece sistematik YFT yetersiz tahminini düzeltir.

Mott yalıtkanları

Kısmen serbest elektron yaklaşımı elektron bant yapısının çoğu özelliğini tanımlayabilse de, bu teorinin bir sonucu, her birim hücre için aynı sayıda elektron sayısını tahmin etmesidir. Eğer elektron sayıları tek ise, her birim hücrede bir çiftleşmemiş elektron bulunmasını bekleriz, ve böylece değerlik bandı tam olarak dolmamış olur ve maddeyi iletken yapar. Ancak CoO gibi maddeler, bu sonuca doğrudan zıt olarak, birim hücrelerinde tek sayıda elektron olmasına rağmen yalıtkandır. Bu tip maddeler Mott yalıtkanı olarak bilinir, ve bu çelişkiyi açıklamak için ek olarak elektron-elektron etkileşimlerinin de detaylandırılması gerekir. Hubbard modeli bu etkileşimleri dahil eden ortalama bir teoremdir.

Diğerleri

Bant yapılarını hesaplamak teorik katı hal fiziğinin önemli bir konusudur. Yukarıda bahsedilen modellere ek olarak diğe modeller şunları içerir:

• Boş kafes yaklaşımı: boş alanın bir bölgesinin “bant yapısı” kafeslere bölünmüştür
• k-p pertürbasyon kuramı: bant yapısının yaklaşık olarak sadece birkaç parametre dahilinde tanımlanmasına imkân veren bir teknik. Bu teknik sıklıkla yarıiletkenler için kullanılır, ve modeldeki parametreler deneylerle belirlenir.
• Kronig-Penney Modeli : bant oluşumunun illüstrasyonu için tek boyutlu dikdörtgensel iyi bir model. Basit olmakla beraber birçok önemli fenomenleri tahmin ediyor, ama nicel değil.
• Hubbard model

Bant yapısı kompleks sayılar olan dalga fonksiyonlarına genellenmiştir, ve bunun sonucunda yüzey ve arayüzleri ile ilgili olan, kompleks bant yapıları olarak adlandırılırlar.

Her model bazı tip katıları çok iyi, bazılarını ise çok zayıf bir biçimde tanımlar. Kısmen serbest elektron modeli metaller için iyiyken, ametaller için yetersiz kalır. Sıkı bağlanma modeli iyonik yalıtkanlar,metal halojenürler gibi (örn.NaCl) için oldukça kesin sonuç verir.

Bant Grafikleri

Gerçek uzayda bant yapılarının Fermi seviyesine göre nasıl değiştiğini anlamak için, genel olarak bant grafiği çizilir. Bu grafikte dikey eksen enerjiyi, yatay eksen ise gerçek uzayı temsil eder. Yatay çizgiler enerji seviyelerini, bloklarsa eneji bantlarını gösterir. Yatay çizgiler eğimli ise, seviyenin veya bandın enerjisi uzaklıkla değişir. Grafiksel olarak, bu durum kristal sistemde bir elektrik alanın bulunduğunu gösterir. Bant grafikleri, birbirileriyle temas halindeyken farklı maddelerin birbirine karşı genel bant yapısı özelliklerini anlamada kullanışlıdır.

Ayrıca bakınız

• Felix Bloch – pioneer in the theory of band structure
• Alan Herries Wilson – pioneer in the theory of band structure

Daha fazla bilgi için

1. Microelectronics, by Jacob Millman and Arvin Gabriel, ISBN 0-07-463736-3, Tata McGraw-Hill Edition.
2. Solid State Physics, by Neil Ashcroft and N. David Mermin, ISBN 0-03-083993-9
3. Elementary Solid State Physics: Principles and Applications, by M. Ali Omar, ISBN 0-201-60733-6
4. Electronic and Optoelectronic Properties of Semiconductor Structures - Chapter 2 and 3 by Jasprit Singh, ISBN 0-521-82379-X
5. Electronic Structure: Basic Theory and Practical Methods by Richard Martin, ISBN 0-521-78285-6
6. Condensed Matter Physics by Michael P. Marder, ISBN 0-471-17779-2
7. Computational Methods in Solid State Physics by V V Nemoshkalenko and N.V. Antonov, ISBN 90-5699-094-2
8. Elementary Electronic Structure by Walter A. Harrison, ISBN 981-238-708-0
9. Pseudopotentials in the theory of metals by Walter A. Harrison, W.A. Benjamin (New York) 1966
10. Tutorial on Bandstructure Methods by Dr. Vasileska (2008)