Görüntü kümesi

Matematikte görüntü kümesi bir fonksiyonun tüm girdi değerlerinin kümesinin veya daha kesin bir söylemle tanım kümesinin tüm elemanlarının fonksiyon tarafından gönderildiği kümedir.

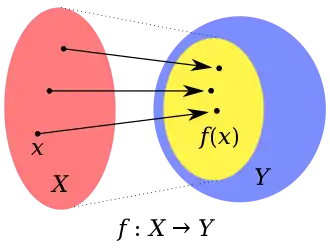
f, X tanım kümesinden Y değer kümesine bir fonksiyon olsun. Y içindeki küçük çember, f kümesinin görüntüsüdür.

Kesin tanım

X ve Y küme, f ise f : X → Y olarak tanımlanmış bir fonksiyon ve x ise X 'in bir elemanı olsun. O zaman, x 'in f altındaki görüntüsü f(x) ile gösterilen ve f 'nin x ile bağdaştırdığı Y kümesinin biricik y elemanıdır. Bir fonksiyonun görüntüsü veya daha kesin bir dille bir fonksiyonun tanım kümesinin görüntüsü, Gör(f) veya İngilizce karşılığı olan image kelimesi sebebiyle Im(f) ile gösterilir. Daha matematiksel bir gösterimle f 'nin görüntü kümesi, $\{f(x):x\in X\}$ kümesidir.[1]

f nin görüntü kümesi değer kümesi ile aynı küme olabilir veya değer kümesinin bir altkümesi olabilir. f örten fonksiyon olmadıkça genelde değer kümesinden daha küçük bir kümedir.

B ⊆ Y kümesinin f altındaki ters görüntü kümesi ise

f^-1[B] = {x ∈ X | f(x) ∈ B}

şeklinde tanımlanır. Bir noktanın, mesela y, görüntüsü f^-1[{y}], ile gösterilir. B 'nin ters görüntü kümesi ise f^-1[B] veya f^-1(B) ile gösterilir. Buradaki f^-1 gösterimi aynı gösterimi kullanan ters fonksiyon ile karıştırılmamalıdır.

Örnekler

1. f: {1,2,3} → {a,b,c,d} fonksiyonu $f(x)=\left\{{\begin{matrix}a,&x=1{\mbox{ ise }}\\d,&x=2{\mbox{ ise }}\\c,&x=3{\mbox{ ise }}.\end{matrix}}\right.$

şeklinde tanımlansın. {2,3} kümesinin f altındaki görüntüsü f({2,3}) = {d,c} olur. f 'nin görüntü kümesi ise {a,d,c} kümesidir. {a,c}'nin ters görüntü kümesi f^-1({a,c}) = {1,3} olur.

2. f: R → R fonksiyonu f(x) = x² şeklinde tanımlansın.

{-2,3} kümesinin f altındaki görüntüsü f({-2,3}) = {4,9}, f 'nin görüntüsü R⁺, {4,9} kümesinin f altındaki ters görüntü kümesi f^-1({4,9}) = {-3,-2,2,3} olur.

Sonuçlar

f : X → Y Xn 'in her A, A₁, ve A₂ altkümesi için ve Y 'nin tüm B, B₁, ve B₂ altkümeleri için şu sonuçlar vardır:

f(A₁ ∪ A₂) = f(A₁) ∪ f(A₂)
f(A₁ ∩ A₂) ⊆ f(A₁) ∩ f(A₂)
f^-1(B₁ ∪ B₂) = f^-1(B₁) ∪ f^-1(B₂)
f^-1(B₁ ∩ B₂) = f^-1(B₁) ∩ f^-1(B₂)
f(f^-1(B)) ⊆ B
f^-1(f(A)) ⊇ A
A₁ ⊆ A₂ → f(A₁) ⊆ f(A₂)
B₁ ⊆ B₂ → f^-1(B₁) ⊆ f^-1(B₂)
f^-1(B^C) = (f^-1(B))^C
(f |_A)⁻¹(B) = A ∩ f^-1(B).

Ayrıca bakınız

Notlar

Smith, William K. Inverse Functions, MacMillan, 1966 (s. 8).

Kaynakça

Artin, Michael (1991), Algebra, Prentice Hall, ISBN 81-203-0871-9
T.S. Blyth, Lattices and Ordered Algebraic Structures, Springer, 2005, ISBN 1-85233-905-5.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Smith, William K. Inverse Functions, MacMillan, 1966 (s. 8).