Hamilton prensibi

Fizikte, Hamilton prensibi, William Rowan Hamilton’un sabit eylem ilkesinin formülasyonudur (tarihsel formülasyonlar için bu makaleye bakın). Fiziksel bir sistemin dinamikleri Lagrange tabanli bir fonksiyonel için varyasyonel bir problemin tarafından belirlenir. Lagrange, sistemi ve üzerine etki eden kuvvetler ile ilgili tüm fiziksel bilgileri içeren bir fonksiyondur. Varyasyonel problemi ise fiziksel sisteminde hareketin diferansiyel denklemlerine eşdeğerdir ve türetilmesini sağlar. Hamilton prensibi klasik mekaniği için formüle edilmiş olsa da elektromanyetik ve yerçekimsel alanlar gibi klasik alanlarda geçerlidir ve hatta kuantum mekaniği, kuantum alan teorisi ve kritiklik teorileri kadar uzatılmıştır.

Matematiksel formülasyonu

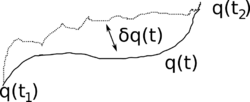
Hamilton ilkesi, bir sistemde ${\displaystyle N}$ genelleştirilmiş koordinatlarla ${\displaystyle \mathbf {q} =\left(q_{1},q_{2},\ldots ,q_{N}\right)}$ tanımlanan gerçek evrimi olan ${\displaystyle \mathbf {q} (t)}$’yi belirtilen iki durum ${\displaystyle \mathbf {q} _{1}\ {\stackrel {\mathrm {def} }{=}}\ \mathbf {q} (t_{1})}$ and ${\displaystyle \mathbf {q} _{2}\ {\stackrel {\mathrm {def} }{=}}\ \mathbf {q} (t_{2})}$ ve belirtilen iki zaman ${\displaystyle t_{1}}$ and ${\displaystyle t_{2}}$ arasında

${\displaystyle {\mathcal {S}}[\mathbf {q} ]\ {\stackrel {\mathrm {def} }{=}}\ \int _{t_{1}}^{t_{2}}L(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt}$.

eylem fonkiyonel’in durgun noktasi (varyasyonu sıfır olan nokta) olduğunu belirtiyor, ki orada ${\displaystyle L(\mathbf {q} ,{\dot {\mathbf {q} }},t)}$ sistemin Lagrange fonksiyonudur. Yani, gerçek evrimin herhangi birinci derece perturbasyonu (en fazla) ikinci derece'ye sonuçlanır, ${\displaystyle {\mathcal {S}}}$'de değişir. ${\displaystyle {\mathcal {S}}}$ eylemi bir fonksiyoneldir, yani, giriş olarak bir fonksiyonu alır ve tek bir skaler numara geri verir. In terms of functional analysis, Hamilton's principle states that the true evolution of a physical system is a solution of the functional equation

${\displaystyle {\frac {\delta {\mathcal {S}}}{\delta \mathbf {q} (t)}}=0}$

Kaynakça

• W.R. Hamilton, "On a General Method in Dynamics.", Philosophical Transaction of the Royal Society Part I (1834) p.247-30827 Eylül 2011 tarihinde Wayback Machine sitesinde arşivlendi.; Part II (1835) p. 95-14427 Eylül 2011 tarihinde Wayback Machine sitesinde arşivlendi.. (From the collection Sir William Rowan Hamilton (1805-1865): Mathematical Papers27 Eylül 2011 tarihinde Wayback Machine sitesinde arşivlendi. edited by David R. Wilkins, School of Mathematics, Trinity College, Dublin 2, Ireland. (2000); also reviewed as On a General Method in Dynamics27 Eylül 2011 tarihinde Wayback Machine sitesinde arşivlendi.)
• Goldstein H. (1980) Classical Mechanics, 2nd ed., Addison Wesley, pp. 35–69.
• Landau LD and Lifshitz EM (1976) Mechanics, 3rd. ed., Pergamon Press. ISBN 0-08-021022-8 (hardcover) and ISBN 0-08-029141-4 (softcover), pp. 2–4.
• Arnold VI. (1989) Mathematical Methods of Classical Mechanics, 2nd ed., Springer Verlag, pp. 59–61.