Harmonik seriler

Harmonik seri ıraksak bir seridir,harmonik sözcüğü ise müzikten devşirilmiştir.

Bir dizinin Harmonik serisi.

${\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots .\!}$

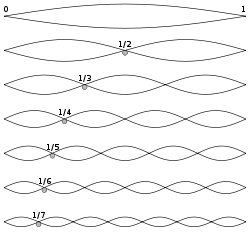
serisini incelersek her kesrin seri toplamında bir payı veya katkısı olduğunu görebiliriz.

Harmonik serinin Iraksaması

Sonsuza çok yavaş olarak ıraksayan bu serinin ilk 10^43 teriminin toplamı en az 100'dür ve Terim terim genişletilirse başka bir ıraksak seriye yakınsar.

${\displaystyle {\begin{aligned}\sum _{k=1}^{\infty }{\frac {1}{k}}&{}=1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{3}}+{\frac {1}{4}}\right]+\left[{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}\right]+\left[{\frac {1}{9}}+\cdots \right]+\cdots \\&{}>1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{4}}+{\frac {1}{4}}\right]+\left[{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right]+\left[{\frac {1}{16}}+\cdots \right]+\cdots \\&{}=1+\ {\frac {1}{2}}\ \ \ +\quad {\frac {1}{2}}\ \quad +\ \qquad \quad {\frac {1}{2}}\qquad \ \quad \ +\quad \ \ {\frac {1}{2}}\ \quad +\ \cdots .\end{aligned}}}$

Bu çok sayıda ¹⁄₂ terimini içeren harmonik serinin sonsuza ıraksadığı açıkça görülüyor. Serinin 2^k-inci kısmı toplamı ${\displaystyle s_{2^{k}}}$ ise

${\displaystyle s_{2^{k}}\geq 1+{k \over 2},}$

(serisine yakınsıyor) Yavaş ve neredeyse logaritmik bir artışa dönüşme var. Bu kanıtı ortaçağ matematikçisi Nicole Oresme bulmuştur,ve o dönemin en ileri seviyesidir. Yine de standart olarak günümüzde bu test kullanılmaktadır. Cauchy testi (kondensasyon) bu testin genelleştirilmiş halidir. Harmonik seri için kullanılan diğer bir yöntem integral ıraksama testi, 1'le sonsuz aralığında ¹⁄_x integralinden faydalanılır. sadece asal sayılar'ın terslerinin toplamı bile exponansiyel bir yavaşlık olmasına rağmen, sonsuza ıraksar ve denemesi daha zordur.

Alternatif yaklaşım

Harmanik serinin toplamına destek için toplamı S ile gösterelim:

${\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots =S}$

kesirlerin yeniden düzenlenmesiyle

${\displaystyle S=\left(1+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+\cdots \right)+\left({\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{6}}+{\frac {1}{8}}+\cdots \right)}$

Basitçe ikinci grubun sonucu

${\displaystyle S=\left(1+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+\cdots \right)+{\frac {1}{2}}\left(1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots \right)}$

ikinci grup yerini S 'e bırakır

${\displaystyle S=\left(1+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+\cdots \right)+{\frac {1}{2}}S}$

Bundan faydalanarak

${\displaystyle {\frac {1}{2}}S=\left(1+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+\cdots \right)}$

veya sonuç;

${\displaystyle {\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{6}}+{\frac {1}{8}}+\cdots =1+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+\cdots }$

Bu doğru olamaz.Arka arkaya gelen bu toplamlar,ıraksamaya götürür.

Diğer bir deneme

geometrik seriler ile başlayalım

${\displaystyle {\frac {1}{1-x}}=1+x+x^{2}+x^{3}+x^{4}+...}$

İki tarafında integrali alınırsa

${\displaystyle -\ln(1-x)=x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}+...}$

iki tarafında ${\displaystyle x\rightarrow 1}$ giderken limitini alırız.

${\displaystyle -\lim _{x\to 1}\ln(1-x)=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+...=\sum _{n=1}^{\infty }{\frac {1}{n}}}$.

${\displaystyle -\lim _{x\to 1}\ln(1-x)=-(-\infty )=\infty }$,den dolayı toplarsak ${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=\infty }$

Diğer bir deyişle toplam ıraksaktır.

Alterne harmonik serinin yakınsaması

Alterne harmonik seride ilk dört kısmi toplam (siyah doğru parçaları) ln2 ye yaklaşıyor (kırmızı hat ).

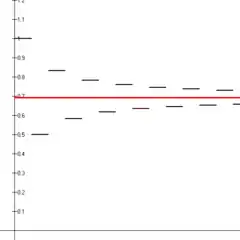
Burada alterne harmonik seri 'nin yakınsaması

${\displaystyle \sum _{k=1}^{\infty }{\frac {(-1)^{k+1}}{k}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\cdots =\ln 2=0.693\,147\,180\,\dots .}$

Bu eşitlik Mercator serisi'nin bir sonucudur., Taylor serisi'nin doğal logaritmadaki ikizidir, diğer eşitlik

${\displaystyle \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{2k+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots =\arctan(1)={\frac {\pi }{4}}.\!}$

Taylor serisi gösteriminin ters tangent fonksiyon sonucu (yarıçap 1'e yakınsama vardır.).

Kısmi toplam

H_n= ${\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k}}}$

serisinde n.nci kısmi toplamı n.nci harmonik sayıyı verir,bu sayı ile doğal logaritma arasında fark Euler-Mascheroni sabiti'ne yakınsar.

Harmonik serinin genelleştirilmesi

Harmonik serinin genel formu

${\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}}.\!}$

burada a ve b sonlu herhangi bir gerçel sayıdır.

P-serisi

p-serisi 'nde p pozitif gerçel bir sayıdır

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}},\!}$

integral testi ile p > 1 için aşırı-harmonik seri, p = 1 için harmonik seri p > 1 seri toplamı ζ(p)'yi yani,Riemann zeta fonksiyonu'nu verir.