Hermit polinomu

Hermit polinomları Pierre-Simon Laplace tarafından 1810'da zor anlaşılır bir biçimde tanımlanmış ve 1859'da Pafnuty Chebyshev tarafından ayrıntılı olarak incelenmiştir. Chebyshev'in çalışmaları göz ardı edildi ve daha sonra, 1864'te polinomlar üzerine yazan ve onları yeni olarak tanımlayan Charles Hermite'den sonra ismi son halini aldı.

Charles Hermite

Tanım

Diğer klasik dik polinomlar gibi, Hermit polinomları birkaç farklı başlangıç noktasından tanımlanabilir. Hermit polinomlarının tam ortak kullanımı olmadığı için iki farklı denklemi vardır.

• Olasılıkçıların kullandığı Hermit polinomu;

${\displaystyle {\textstyle He_{n}(x)=(-1)^{n}e^{\left({\frac {x^{2}}{2}}\right)}{d^{n} \over dx^{n}}e^{\left(-{\frac {x^{2}}{2}}\right)}}}$

• Fizikçilerin kullandığı Hermit polinomu;

${\displaystyle {\displaystyle H_{n}(x)=(-1)^{n}e^{x^{2}}{d^{n} \over dx^{n}}e^{-x^{2}}}}$

Bu denklemler bir Rodrigues formülü biçimindedir ve şu şekilde de yazılabilir;

${\displaystyle {\displaystyle {\mathit {He}}_{n}(x)=\left(x-{\frac {d}{dx}}\right)^{n}\cdot 1,\quad H_{n}(x)=\left(2x-{\frac {d}{dx}}\right)^{n}\cdot 1.}}$

İki tanım tam olarak aynı değildir, her biri bir diğerinin yeniden ölçeklendirilmesidir.

${\displaystyle {\displaystyle H_{n}(x)=2^{\frac {n}{2}}{\mathit {He}}_{n}\left({\sqrt {2}}\,x\right),\quad {\mathit {He}}_{n}(x)=2^{-{\frac {n}{2}}}H_{n}\left({\frac {x}{\sqrt {2}}}\right).}}$

Hermit polinomunun ilk altı değer grafiği

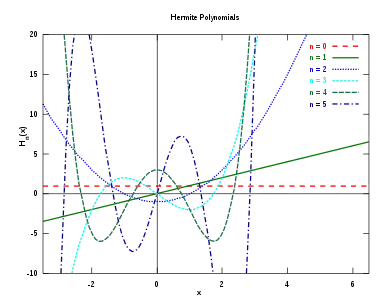
Olasılıkçıların kullandığı Hermit polinomunun ilk on bir değeri;

${\textstyle {\displaystyle He_{0}(x)=1}}$

${\textstyle {\displaystyle He_{1}(x)=x}}$

${\textstyle {\textstyle He_{2}(x)=x^{2}-1}}$

${\textstyle {\textstyle He_{3}(x)=x^{3}-3x}}$

${\textstyle {\textstyle He_{4}(x)=x^{4}-6x^{2}+3}}$

${\textstyle {\textstyle He_{5}(x)=x^{5}-10x^{3}+15x}}$

${\textstyle {\textstyle He_{6}(x)=x^{6}-15x^{4}+45x^{2}-15}}$

${\textstyle {\textstyle He_{7}(x)=x^{7}-21x^{5}+105x^{3}-105x}}$

${\textstyle {\textstyle He_{8}(x)=x^{8}-28x^{6}+210x^{4}-420x^{2}+105}}$

${\textstyle {\textstyle He_{9}(x)=x^{9}-36x^{7}+378x^{5}-1260x^{3}+945x}}$

${\textstyle {\textstyle He_{10}(x)=x^{10}-45x^{8}+630x^{6}-3150x^{4}+4725x^{3}-945}}$

Fizikçilerin(${\displaystyle H_{n}}$) kullandığı Hermit polinomunun ilk altı değer grafiği

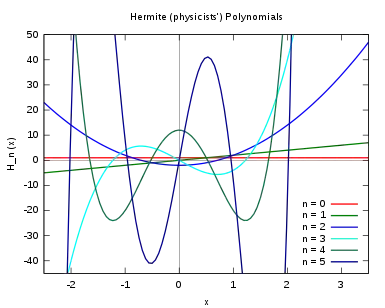
Fizikçilerin kullandığı Hermit polinomunun ilk on bir değeri;

${\textstyle H_{0}(x)=1}$

${\displaystyle H_{1}(x)=2x}$

${\textstyle H_{2}(x)=4x^{2}-2}$

${\textstyle H_{3}(x)=8x^{3}-12x}$

${\textstyle H_{4}(x)=16x^{4}-48x^{2}+12}$

${\textstyle H_{5}(x)=32x^{5}-160x^{3}+120}$

${\textstyle H_{6}(x)=64x^{6}-480x^{4}+720x^{2}-120}$

${\textstyle H_{7}(x)=128x^{7}-1344x^{5}+3360x^{3}-1680x}$

${\textstyle H_{8}(x)=256x^{8}-3584x^{6}+13440x^{4}-13440x^{2}+1680}$

${\textstyle H_{9}(x)=512x^{9}-9216x^{7}+48384x^{5}-80640x^{3}+30240x}$

${\textstyle H_{10}(x)=1024x^{10}-2340x^{8}+161280x^{6}-403200x^{4}+302400x^{2}-30240}$

Özellikleri

${\displaystyle n}$ dereceden bir Hermit polinomu ${\displaystyle n}$ dereceli bir polinomdur. Olasılıkçıların( ${\displaystyle He_{n}}$) kullandığı Hermit polinomunun ilk terimindeki katsayısı her zaman 1'dir.Fizikçilerin(${\displaystyle H_{n}}$) kullandığı Hermit polinomunun katsayısı ${\displaystyle 2^{n}}$

Örnek

Olasılıkçıların kullandığı Hermit polinomunun ${\displaystyle n}$'i 2 olsun ve aradaki farkı anlayabilmek için fizikçilerin kullandığı Hermit polinomunun da ${\displaystyle n}$'i 2 olsun

${\displaystyle {\textstyle {\textstyle He_{2}(x)=x^{2}-1}}}$ ilk terimin katsayısı 1 ${\textstyle H_{2}(x)=4x^{2}-2}$ ilk terimin katsayısı 4(${\displaystyle 2^{2}=4}$)

Diklik

${\displaystyle He_{n}}$ ve  ${\displaystyle H_{n}}$ dereceden polinomları için ${\displaystyle n=1,2,3,4........}$ Bu polinomlar ağırlık işlevine(fonksiyon) göre dikliktir.

${\displaystyle {\displaystyle w(x)=e^{\left({\frac {x^{2}}{2}}\right)}}}$ (${\displaystyle He}$ için)

ya da

${\displaystyle {\displaystyle w(x)=e^{-x^{2}}}}$ (${\displaystyle H}$ için)