Küresel üçgen

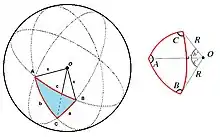
Küresel üçgen, bir kürenin yüzeyinde, üç köşede çiftler halinde kesişen üç büyük dairesel yay tarafından oluşturulan bir şekildir. Riemann teoremi ile açıklanır. Küresel üçgen, düzlemsel üçgenin küresel analogudur ve bazen Euler üçgeni olarak adlandırılır (Harris ve Stocker 1998). Küresel üçgenin açıları A, B ve C (kürenin yüzeyi boyunca köşelerde radyan olarak ölçülmüştür) ve küresel üçgenin oturduğu kürenin yarıçapı R olsun. Küresel üçgenin yüzey alanı (Δ);

Küresel Üçgen

Δ = R²[(A+B+C)-π] = R²E

E küresel fazlalık olmak üzere ve düzlemsel üçgenin dejenere durumunda E = 0 olacak şekilde hesaplanır.

Küresel bir üçgenin açılarının toplamı π ile 3π radyan arasındadır (180° ile 540°; Zwillinger 1995, s. 469). 180°yi aştığı miktara küresel fazlalık denir ve E veya Δ olarak gösterilir; ikincisi, küresel bir üçgenin yüzey alanına da atıfta bulunabileceğinden kafa karışıklığına neden olabilir. 2π radyan (360°) ile a, b ve c yan yay uzunluklarının toplamı arasındaki fark küresel kusur olarak adlandırılır ve D veya δ olarak gösterilir.

Herhangi bir küre üzerinde, üç bağlantı yayı çizilirse, iki üçgen oluşturulur. Her bir üçgen bir yarım küreyi kaplarsa, boyutları eşittir, ancak genel olarak biri daha büyük ve biri daha küçük olacaktır. Herhangi bir küresel üçgen bu nedenle hem iç hem de dış üçgen olarak kabul edilebilir ve genellikle iç üçgen varsayılır. Dış küresel üçgenin açılarının toplamı 3π ile 5π radyan arasındadır.

Bir küre üzerindeki şekillerin açılarının ve mesafelerinin incelenmesi küresel trigonometri olarak bilinir.

Kaynakça

Harris, J. W. and Stocker, H. "General Spherical Triangle." §4.9.1 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, s.108-109, 1998.
Zwillinger, D. (Ed.). "Spherical Geometry and Trigonometry." §6.4 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, s.468-471, 1995.