Kelebek önsavı

matematikte,Kelebek önsavı veya Zassenhaus önsavı, Hans Zassenhaus adına ithaf edilir,bir grubunun altgrupların kafesinin veya bir modülün altmodullerin kafesinin, veya daha genel herhangi moduler kafes için teknik bir sonuçtur.[1]

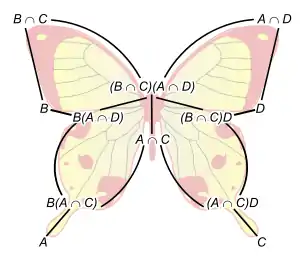
Zassenhaus Hasse diagramı "kelebek" önsavı - daha küçük altgrupları diyagramın üst kısmına doğrudur

Önsav: Varsayım ${\displaystyle (G,\Omega )}$ bir grup ile operatorlerinin ve ${\displaystyle A}$ ve ${\displaystyle C}$altgruplarıdır. Varsayım

${\displaystyle B\triangleleft A}$ ve ${\displaystyle D\triangleleft C}$

kararlı altgruplarıdır. Öyleyse,

${\displaystyle (A\cap C)B/(A\cap D)B}$ ifadesi ${\displaystyle (A\cap C)D/(B\cap C)D.}$ ya eşyapıdır

Schreier arıtma teoremi'nin verilen sorunsuz kanıtını Zassenhaus önsavının özelliği sağlar.İlgili çeşitli grupların çizilen Hasse diagramına çalışırken 'kelebek' belirginleşir.

Notlar

1. See Pierce, p. 27, exercise 1.

Kaynakça

• Pierce, R. S. (1982), Associative algebras, Springer, s. 27, ISBN 0-387-90693-2.
• Goodearl, K. R.; Warfield, Robert B. (1989), An introduction to noncommutative noetherian rings, Cambridge University Press, ss. 51, 62, ISBN 978-0-521-36925-1.
• Lang, Serge, Algebra, Graduate Texts in Mathematics (Revised 3rd bas.), Springer-Verlag, ss. 20-21, ISBN 978-0-387-95385-4.
• Carl Clifton Faith, Nguyen Viet Dung, Barbara Osofsky (2009) Rings, Modules and Representations. p. 6. AMS Bookstore, ISBN 0-8218-4370-2
• Hans Zassenhaus (1934) "Zum Satz von Jordan-Hölder-Schreier", Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 10:106–8.
• Hans Zassenhaus (1958) Theory of Groups, second English edition, Lemma on Four Elements, p 74, Chelsea Publishing.

Dış bağlantılar

• Zassenhaus Lemma and proof at http://www.artofproblemsolving.com/Wiki/index.php/Zassenhaus%27s_Lemma4+Haziran+2008+tarihinde+Wayback+Machine+sitesinde+arşivlendi.