Mekanik enerji

Fizikte mekanik enerji, mekanik bir sistemin bileşenlerinde yer alan potansiyel ve kinetik enerjinin toplamı olarak ifade edilir. Bu enerji cismin hareketi ve konumu ile ilişkilidir. İdeal bir ortamda eğer bir cisim, yalnızca yer çekimi kuvveti gibi konservatif bir kuvvete tabi ise enerjinin korunumu yasası mekanik enerjinin sabit olduğunu söyler. Bir cisim konservatif net kuvvetin tersi yönünde hareket ederse potansiyel enerji artacak ve eğer sürati (hızı değil) de değiştiyse kinetik enerjisi de değişecektir. Tüm gerçek sistemlerde sürtünme kuvveti gibi konservatif olmayan kuvvetler bulunacaktır, fakat bu değerler çoğu zaman ihmal edilebilir ve mekanik enerjinin yine de sabit olduğu söylenebilir. Esnek çarpışmalarda mekanik enerji korunurken esnek olmayan çarpışmalarda bir kısmı ısıya dönüşür. Kayıp mekanik enerji ile sıcaklıktaki artış arasındaki ilişkiyi James Prescott Joule keşfetmiştir.

Bir mekanik sistem örneği: Bir uydu, Dünya’nın etrafında konservatif yer çekimi kuvvetinin etkisiyle dönmektedir, kuvvet konservatif olduğu için mekanik enerji de korunmaktadır. Uydu, dolandığı yörüngeye dik bir şekilde Dünya'nın merkezine doğru hızlanmakta. Şekilde ivme, yeşil vektör ile gösterilirken hız da kırmızı vektör ile gösterilmiştir. Hız, vektörün yönüne bağlı olarak sürekli değişirken vektörün şiddeti değişmediği için sürat sabit kalır.

Bugün elektrik motoru, buhar makinesi vb. araçlar elektriksel potansiyel enerji, ısı gibi enerji türlerini mekanik enerjiye dönüştürür.

Genel Formulü

Enerji skaler bir büyüklüktür ve bir sistemin mekanik enerjisi; konumu ile ölçülen potansiyel enerjisi ile hareketiyle ölçülen kinetik enerjisinin toplamına eşittir:[1][2]

${\displaystyle E_{mekanik}=U+K\,}$

Eğer bir cisim ya da sistem yalnızca konservatif kuvvetlerin etkisindeyse, mekanik enerjinin korunumu yasası bu cisim ya da sistemin toplam mekanik enerjinin sabit olduğunu ifade eder.[3] Konservatif ile konservatif olmayan kuvvet arasındaki fark şöyle açıklanabilir: Konservatif bir kuvvetin bir cismi bir yerden bir yere götürürken yaptığı iş yoldan bağımsız iken, konservatif olmayan bir kuvvet bir cisme etki ettiğinde bu kuvvet tarafından yapılan iş yoldan bağımsız değildir.[4]

Potansiyel enerji, U, konservatif bir kuvvete tabi olan bir cismin konumuna bağlıdır. Bir cismin iş yapabilme yeteneği olarak tanımlanır ve üzerine etki eden net kuvvetin tersi yönünde ilerledikçe büyüklüğü artar.[nb 1][1] Eğer F konservatif bir kuvveti ve x de yolu temsil ederse; kuvvetin x₁ ve x₂ arasındaki potansiyel enerjisi F'in x₁'den x₂'ye negatif integrali olarak tanımlanır:[6]

${\displaystyle U=-\int \limits _{x_{1}}^{x_{2}}{\vec {F}}\cdot d{\vec {x}}}$

Kinetik enerji, K, cismin süratine bağlıdır ve başka bir cisme çarptığında o cisim üzerinde iş yapabilme yeteneğidir.[nb 2][10] Cismin kütlesinin yarısı ile süratinin karesinin çarpımı olarak tanımlanır. Cisimlerden oluşan bir sistemin toplam kinetik enerjisi bu cisimlerin ayrı ayrı kinetik enerjileri toplamına eşittir:[1][11]

${\displaystyle K={1 \over 2}mv^{2}}$

Enerjinin korunumu ve dönüşümü

Enerjinin korunumu yasası, klasik mekaniğin üç korunum yasası arasında en önemlisi olarak değerlendirilir.[nb 3] Bu yasaya göre ideal bir sistemin mekanik enerjisi, cisimlerin çarpışması sırasında oluşabilecek iç sürtünmeler de buna dahil olmak üzere, sürtünme kuvvetlerinden bağımsız olduğu sürece zaman içerisinde sabit kalır. Gerçekte, sürtünme kuvvetleri ve diğer konservatif olamayan kuvvetler her zaman mevcuttur fakat çoğu zaman bu kuvvetlerin etkisi yok denecek kadar azdır ve mekanik enerjinin korunumu ilkesi makul bir yaklaşık değerle kabul edilebilir. İdeal bir sistemde enerji, yoktan var ya da vardan yok edilemese de başka enerji türlerine dönüştürülebilir.[1][12]

Hız vektörü (yeşil) ve ivme vektörü (mavi) ile gösterilen bir sarkaç. Hız vektörünün şiddeti, yani sürat, dikey konumda en yüksek değerini alır. Sarkaç da en uç noktalarda Yeryüzü'nden en uzak konumuna ulaşır.

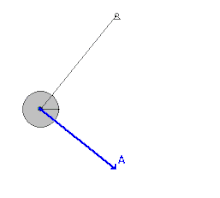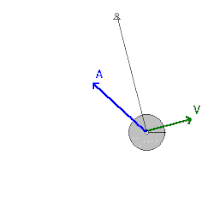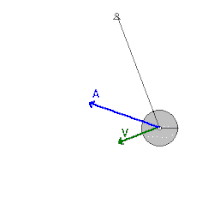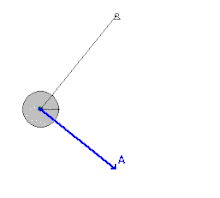
Bu yüzden, havanın direnç kuvveti ve mildeki sürtünmenin ihmal edilebildiği sallanan sarkaç gibi konservatif yer çekimi kuvvetine tabi tutulan mekanik sistemlerde, enerji; kinetik ve potansiyel olarak birbirine dönüşür ve asla sistemi terketmez. Sarkaç dikey konumdayken Yeryüzü'ne en yakın noktada olması ve süratinin en yüksek olması nedeniyle en yüksek kinetik enerji, en düşük potansiyel enerjiye bu konumda sahip olur. Diğer bir açıdan, sarkaç; salınımın en uç noktalarına ulaştığında sürati sıfır olacağından ve Yeryüzü'nden en uzak noktaya varacağından bu konumda kinetik enerjisi en düşük ve potansiyel enerjisi de en yüksek değerini alır. Fakat işin içine sürtünme kuvvetleri dahil edildiğinde, sarkaç bu konservatif olmayan kuvvetlere karşı koymak için iş yapacağından, sistem her salınımda mekanik enerji kaybedecektir.[2]

Sistemdeki bu tarz bir enerji kaybının sıcaklık değerini artırdığı amatör fizikçi James Prescott Joule tarafından keşfedildi. Fizikçi, sürtünmeye karşı yapılan belli bir miktarda işin belirli bir ısı değerine dönüştüğünü deneysel olarak ispatladı.[13] Mekanik enerji ile ısı arasındaki bu denklik, çarpışan cisimler göz önüne alındığında oldukça önemlidir. Esnek çarpışmada enerji korunur, yani çarpışan cisimlerin kinetik enerjileri toplamı çarpışmadan önce ve sonra aynıdır. Fakat esnek olmayan bir çarpışmadan sonra sistemin toplam mekanik enerjisi değişir. Genelde çarpışmadan sonraki toplam mekanik enerji, ilk toplam mekanik enerjiden düşüktür ve kayıp kısım ısıya dönüşür. Fakat yine de esnek olmayan bir çarpışmadan sonra, örneğin çarpışma kimyasal enerjinin mekanik enerjiye dönüşmesine neden olmuşsa, son mekanik enerji daha büyük çıkabilir.

Dönüşümü

Günümüzde birçok teknolojik araç mekanik enerjiyi diğer enerji türlerine ya da aksi yönde dönüştürebilmektedir.

• Elektrik motoru, elektrik enerjisini mekanik enerjiye çevirir.[14][15][16]
• Jeneratör, mekanik enerjiyi elektrik enerjisine dönüştürür.[17]
• İçten yanmalı motor, yakıt yakarak kimyasal enerjiden mekanik enerji elde eden bir ısı motorudur. Bu motor bu mekanik enerjiden genellikle elektrik üretir.[18]
• Buhar makinesi, buharın ısı enerjisini mekanik enerjiye dönüştürür.[19]
• Türbin, gaz ya da sıvı bir akımının kinetik enerjisini mekanik enerjiye dönüştürür.[20]

Diğer türlerden ayrılışı

Farklı enerji türleri farklı doğa bilimlerinin sınırları içerisinde incelenir.

• Kimyasal enerji, kimyasal bağların sahip olduğu bir nevi potansiyel enerjidir ve kimya dalı içerisinde incelenir.[21]
• Nükleer potansiyel enerji, atom çekirdeğindeki enerjidir ve çekirdek fiziği sınırları içerisinde incelenir.[22]
• Elektromanyetik enerji; elektrik yükü, manyetik alan ve foton formundadır. Elektromanyetizma çerçevesinde incelenir.[23][24]
• Kuantum mekaniğindeki çeşitli enerji formları, örn. bir atomdaki elektronların enerji seviyeleri.[25][26]

Kaynakça

Notlar

1. It is important to note that when measuring mechanical energy, an object is considered as a whole, as it is stated by Isaac Newton in his Principia: "The motion of a whole is the same as the sum of the motions of the parts; that is, the change in position of its parts from their places, and thus the place of a whole is the same as the sum of the places of the parts and thereore is internal and in the whole body."[5]
2. Fizikte, sürat skaler; hız vektörel bir niceliktir. Yani hız yönü olan bir büyüklük iken sürat bu vektörel niceliğin şiddetidir.[7][8][9]
3. Diğer korunum yasaları çizgisel momentumun korunumu ve Açısal momentumun korunumudur.[1]

Referanslar

1. Wilczek, Frank (2008). "Conservation laws (physics)". AccessScience. McGraw-Hill Companies. Erişim tarihi: 26 Ağustos 2011.
2. "mechanical energy". The New Encyclopædia Britannica: Micropædia: Ready Reference. 7 (15th bas.). 2003.
3. Jain 2009, s. 12
4. Department of Physics. "Review D: Potential Energy and the Conservation of Mechanical Energy" (PDF). Massachusetts Institute of Technology. 8 Ocak 2016 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 3 Ağustos 2011.
5. Newton 1999, s. 409
6. "Potential Energy". Texas A&M University–Kingsville. 14 Nisan 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 25 Ağustos 2011.
7. Brodie 1998, ss. 129–131
8. Rusk, Rogers D. (2008). "Speed". AccessScience. McGraw-Hill Companies. Erişim tarihi: 28 Ağustos 2011.
9. Rusk, Rogers D. (2008). "Velocity". AccessScience. McGraw-Hill Companies. Erişim tarihi: 28 Ağustos 2011.
10. Brodie 1998, s. 101
11. Jain 2009, s. 9
12. E. Roller, Duane (2008). "Conservation of energy". AccessScience. McGraw-Hill Companies. Erişim tarihi: 26 Ağustos 2011.
13. "James Prescott Joule". Scientists: Their Lives and Works. Gale. 2006. as cited on "Student Resources in Context". Gale. 3 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Ağustos 2011.
14. Kopicki, Ronald J. (2003). "Electrification, Household". Kutler, Stanley I. (Ed.). Dictionary of American History. 3 (3rd bas.). New York: Charles Scribner's Sons. ss. 179-183. as cited on "Student Resources in Context". Gale. 3 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Eylül 2011.
15. Lerner, K. Lee; Lerner, Brenda Wilmoth, (Ed.) (2008). "Electric motor". The Gale Encyclopedia of Science (4th bas.). Detroit: Gale. as cited on "Student Resources in Context". Gale. 3 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Eylül 2011.
16. "Electric motor". U*X*L Encyclopedia of Science. U*X*L. 2007. as cited on "Student Resources in Context". Gale. 3 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Eylül 2011.
17. "Generator". U*X*L Encyclopedia of Science. U*X*L. 16 Temmuz 2007. Tarih değerini gözden geçirin: Tarih ve yıl parametreleri birlikte kullanılmamalı (yardım); as cited on "Student Resources in Context". Gale. 3 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Ekim 2011.
18. Lerner, K. Lee; Lerner, Brenda Wilmoth, (Ed.) (2008). "Internal combustion engine". The Gale Encyclopedia of Science (4th bas.). Detroit: Gale. as cited on "Student Resources in Context". Gale. 3 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Ekim 2011.
19. "Steam engine". U*X*L Encyclopedia of Science. U*X*L. 16 Temmuz 2007. Tarih değerini gözden geçirin: Tarih ve yıl parametreleri birlikte kullanılmamalı (yardım); as cited on "Student Resources in Context". Gale. 3 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Ekim 2011.
20. Lerner, K. Lee; Lerner, Brenda Wilmoth, (Ed.) (2008). "Turbine". The Gale Encyclopedia of Science (4th bas.). Detroit: Gale. as cited on "Student Resources in Context". Gale. 3 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Ekim 2011.
21. Atkins, Peter W. (2008). "Chemical energy". AccessScience. McGraw-Hill Companies. Erişim tarihi: 17 Ekim 2011.
22. Duckworth, Henry E. (2008). "Nuclear binding energy". AccessScience. McGraw-Hill Companies. Erişim tarihi: 17 Ekim 2011.
23. Hartwig, William H. (2008). "Electrical energy measurement". AccessScience. McGraw-Hill Companies. Erişim tarihi: 17 Ekim 2011.
24. Smythe, William R. (2008). "Electromagnetic radiation". AccessScience. McGraw-Hill Companies. Erişim tarihi: 17 Ekim 2011.
25. Gerjuoy, Edward (2008). "Quantum mechanics". AccessScience. McGraw-Hill Companies. Erişim tarihi: 17 Ekim 2011.
26. March-Russell, John (2008). "Energy level (quantum mechanics)". AccessScience. McGraw-Hill Companies. Erişim tarihi: 17 Ekim 2011.

Bibliyografya

• Brodie, David; Brown, Wendy; Heslop, Nigel; Ireson, Gren; Williams, Peter (1998). Terry Parkin (Edl.). Physics. Addison Wesley Longman Limited. ISBN 978-0582279844 |isbn= değerini kontrol edin: checksum (yardım).
• Jain, Mahesh C. (2009). Textbook of Engineering Physics, Part I. New Delhi: PHI Learning Pvt. Ltd. ISBN 978-8120338623. Erişim tarihi: 25 Ağustos 2011.
• Newton, Isaac (1999). I. Bernard Cohen, Anne Miller Whitman (Edl.). The Principia: mathematical principles of natural philosophy. United States of America: University of California Press. ISBN 978-0520088160.