Nyquist frekansı

Elektronik mühendisi Harry Nyquist'in adını alan Nyquist frekansı, ayrık bir sinyal işleme sisteminin örnekleme oranının yarısıdır.[1] Bazen bir örnekleme sisteminin katlanma frekansı olarak bilinir.[2]

Açıklama
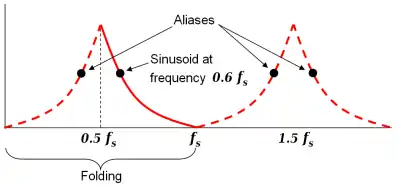
Siyah noktalar birbirinin eşdeşidir. Düz kırmızı çizgi frekansa göre değişen genliğin bir örneğidir. Kesikli kırmızı çizgiler eşdeşlere karşılık gelen yollardır.

Resimdeki örnekte, örnekleme frekansı fs, buna karşılık gelen Nyquist frekansı 0.5 fs'dir. 0.6 fs'deki siyah nokta, örnekleme frekansının %60'ı kadar frekansa sahip bir sinüs fonksiyonunun genliği ve frekansını göstermektedir. Diğer üç siyah nokta da, örneklenen gerçek sinüzoid ile aynı örnek setini üretecek olan diğer üç sinüzoidin frekanslarını ve genliklerini gösterir. Kırmızı çizgiler, sinüs fonksiyonunun frekansı fs/2'den fs'e kadar artılırken siyah noktaların takip edeceği yollardır. Bu işlemin sonucunda ortaya çıkan simetri noktası (resimde yaklaşık 0.5 fs) katlama olarak adlandırılır.

Nyquist frekansı Nyquist hızı ile karıştırılmamalıdır, ikincisi belirli bir sinyal veya sinyal ailesi için Nyquist örnekleme kriterini karşılayan minimum örnekleme oranıdır. Nyquist oranı, örneklenmekte olan fonksiyonun maksimum bileşen frekansının iki katıdır. Örneğin, sinüsoid için Nyquist oranı 0.6'da fs 1,2'dir fs, yani fs hızında örneklenmemiş demektir . Dolayısıyla, Nyquist oranı sürekli zaman sinyalinin bir özelliğidir, oysa Nyquist frekansı ayrık zamanlı bir sistemin özelliğidir.[3][4]

Fonksiyon alanı zaman olduğunda, örnekleme hızları genellikle saniyedeki örneklerle ifade edilir ve Nyquist frekans birimi saniyedeki devirdir ( hertz ). Bir görüntü örnekleme sisteminde olduğu gibi fonksiyon alanı mesafe olduğunda, örnekleme hızı inç başına nokta olabilir ve karşılık gelen Nyquist frekansı döngü / inç cinsinden olur.

Aliasing

Tekrar Şekil 1'e atıfta bulunarak, sinüsoidin 0.6 fs da örneklenmesi , aynı örnek kümesini üreten farklı bir fonksiyon olan daha düşük frekanslı bir diğer ad olmasına izin verir. Bu durum genellikle örtüşme olarak tanımlanır. Tipik olarak numunelerinden sürekli bir fonksiyon oluşturmak için kullanılan matematiksel algoritmalar, örneklenmemiş frekans bileşenlerinin katkılarını yanlış yorumlayarak bozulmaya neden olur. Saf 0.6 fs örnekleri sinüs eğrisi yerine sinusoid 0,4 fs üretir. Gerçek frekans 0,4 fs olsaydı 0.6, 1.4, 1.6, vs.'de hala aliasing olacaktır, [note 1] ancak yeniden yapılandırılmış frekans doğru olacaktır.

Tipik bir örnekleme uygulamasında, ilk önce beklenen içeriğe (ses, müzik, vb.) Ve istenen aslına bağlı olarak korunacak ve yeniden oluşturulacak en yüksek frekans seçilir. Ardından örnekleyicinin önüne bir kenar yumuşatma filtresi yerleştirilir . Görevi, bu sınırın üzerindeki frekansları zayıflatmaktır. Son olarak, filtrenin özelliklerine dayanarak, kabul edilebilir derecede az miktarda örtüşme sağlayacak bir örnekleme hızı (ve karşılık gelen Nyquist frekansı) seçilir.

Numune hızının önceden belirlendiği uygulamalarda, filtre, tersi yerine Nyquist frekansına göre seçilir. Örneğin, ses CD'lerinin örnekleme hızı 44100 mwUA örnek sayısı/sn. Nyquist frekansı bu nedenle 22050 Hz dir. Kenar yumuşatma filtresi daha yüksek frekansları yeterince bastırmalı, ancak insan işitme aralığındaki frekansları ihmal edilebilir şekilde etkilemelidir. 0–20 kHz koruyan bir filtre bunun için fazlasıyla yeterlidir.

Diğer anlamları

Nyquist frekansı teriminin yukarıda belirtilenler gibi erken kullanımlarının tümü bu makalede sunulan tanımla tutarlıdır. Bazı saygın ders kitapları da dahil olmak üzere daha sonraki bazı yayınlar, Nyquist frekansının iki katı sinyal bant genişliğini çağırır;[5][6] bu belirgin bir şekilde azınlık kullanımıdır ve sinyal bant genişliğinin iki katındaki frekans aksi halde Nyquist oranı olarak adlandırılır.

Notlar
  1. As previously mentioned, these are the frequencies of other sinusoids that would produce the same set of samples as the one that was actually sampled.

Kaynakça
  1. Cramér, Harald (1959). Probability and Statistics: The Harald Cramér Volume. Almqvist & Wiksell.
  2. "An Introduction to Sampling Theory". 1 Eylül 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Nisan 2010. Frequencies "fold" around half the sampling frequency - which is why [the Nyquist] frequency is often referred to as the folding frequency.
  3. James J. Condon; Scott M. Ransom (5 Nisan 2016). Essential Radio Astronomy (İngilizce). Princeton University Press. ISBN 9781400881161.
  4. John W. Leis (14 Ekim 2011). Digital Signal Processing Using MATLAB for Students and Researchers (İngilizce). John Wiley & Sons. ISBN 9781118033807.
  5. Jonathan M. Blackledge; Martin Turner (2003). Digital Signal Processing (İngilizce). ISBS. ISBN 1-898563-48-9.
  6. Paulo S. R. Diniz; Eduardo A. B. da Silva; Sergio L. Netto (18 Nisan 2002). Digital Signal Processing (İngilizce). Cambridge University Press. ISBN 0-521-78175-2.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.