Parçacık fiziği ve temsil teorisi
Parçacık fiziği ve gösterim teorisi arasındaki bağlantı temel parçacık ve Lie grupları ve Lie cebiri yapısı özellikleri arasında ilk Eugene Wigner tarafından 1930'larda kaydedilen doğal bir bağlantı vardır. Bu bağlama göre, bir temel parçacığın farklı kuantum durumları Poincaré grubunun bir indirgenemez gösterimini doğurur. Dahası, onların spektrumları dahil çeşitli parçacıklar, ve özellikleri evrenin "yaklaşık simetrileri"ne karşılık, Lie cebiri gösterimleri ile ilgili olabilir.
| Parçacık fiziğinin standart modeli |
|---|
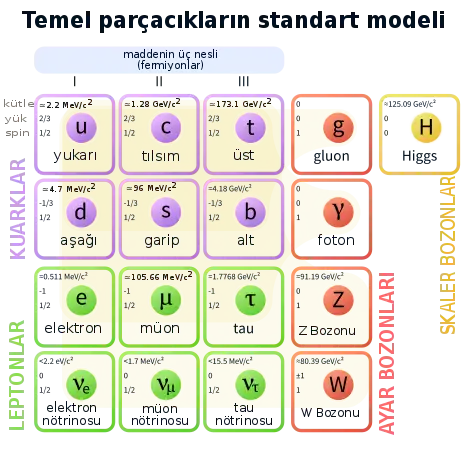 |
|
Sınırları |
Genel Resim
Kuantum mekaniği( belirli bir momentum dağılımı , yer dağılımı , spin durumu , vb ) herhangi bir parçacık , varolabilir parçacıkların ne tür olduğunu anlamanıza yardımcı olmak için , bir Hilbert uzayı H. bir vektörü ( ya da "ket" ) olarak yazılır Bu şekilde, H, ve bunların özellikleri için olanakları sınıflandırmak çok önemlidir. (Bir "Faz faktörü" ile farklılık veya fizik terminolojisinde , iki " ketler " ) skalar çarpan ile farklılık gösteren iki vektör aynı fiziksel durumuna karşılık gelen kuantum Başlangıcı parçacık daha kesin olarak, ilişkili yansıtmalı Hilbert uzayı PH ile karakterize edilir. Diyelimki G evrenin simetri grubu olsun ve fizik yasaları değişmez olduğu altında simetrilerin kümesidir . ( Örneğin, G bir unsuru beş saniye ile zaman içinde ileriye tüm parçacıkların ve alanların simültane ötelemesi . ) belirli bir ket durumundaki parçacık ile başlayarak ve G içinde bir simetri dönüşüm g , bu mümkün yeni bir durum ket almak için parçacığa simetri dönüşümü uygulamak için . Bu resmin tutarlı olması için, PH Gnin bir projektif grup temsili olması gereklidir ( bir simetri dönüşüm uygulayarak , daha sonra ters dönüşüm uygulayarak ,özgün kuantum durumunu geri edeceğini Örneğin, bu durum garanti.) Bu nedenle, herhangi bir tanecik , bir izdüşümsel PH vektör uzayı G 'nin eşsiz bir gösterimi ile ilişkilidir. (Bu parçacık "yatmaktadır" demek, ya da gösterimsel "olarak dönüştürür.") Çok önemli durumda, partikül (daha özel), altta yatan Gnin bir grup gösterimi ile ilgili (izdüşümsel olmayan olduğu da gösterilebilir) uzay H.[1] Wigner teoremi bir üniter temsilidir,ya da muhtemelen anti- üniter kanıtlıyor.[1] Bu yüzden G 'nin her tür parçacığın bir temsile karşılık , ve eğer biz G grup temsilleri sınıflandırabilirsek ,biz bulunabilir parçacıkların ne tür dolayısıyla H olanakları ve özellikleri hakkında çok daha fazla bilgiye sahip olacak.
Poincaré grubu
ötelemenin grupları ve Lorentz dönüşümleri Poincaré grubu formu, ve bu grup kesinlikle Gnin bir altgrubudur (neglecting general görelilik etkileri ihmal ediliyor , veya diğer bir deyişle düz uzay) içinde. bundan dolayı, Gnin herhangi gösterimi özel olarak Poincaré grubun bir gösterimi olacak olsun. Poincaré grubunun gösterimi bir negatif olmayan kütle ile karakterize edilen birçok durum içindedir ve bir yarı-tam sayı spin (bakınızWigner sınıflandırması); bu parçacıklarının nedeni olarak düşünülebilen spin nicelemesi vardır. (unutmadan burada aslında diğer olası takyonlar gibi gösterimlerdir,bu bazı durumları içinde öte-parçacıkların veya sabit kütlenin spin nicelemesi yoktur.)
Diğer simetriler
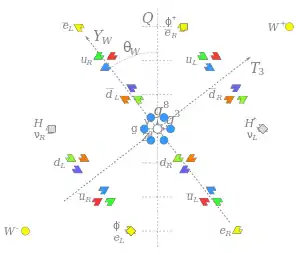
Böylece uzay-zaman simetrileri Poincaré grup içinde görselleştirmek için özellikle kolaydır ve inanılan budur, burada ayrıca simetrilerin diğer tiplerine ve içsel simetriler denir. Tek örnekleri renktir SU(3), üç kuark renklerinin sürekli arayüküne karşılık gelen bir tam simetridir.
Örnek: izospin simetri
Gerçek dünyadan bir örnek izospin simetridir, bir SU(2) grup yukarı kuarklar ve aşağı kuarklar arasındaki benzerliğe karşı gelir. Bu bir yaklaşık simetridir: Yukarı ve aşağı kuarklar onlar güçlü kuvvet altında etkileşim böyle özdeş olmakla birlikte, onların farklı kütleleri ve farklı elektrozayıf etkileşimleri vardır. Mathematiksel olarak, burada bir soyut iki-boyutlu vektör uzayı
ve fiziğin kanunları bu uzaya fizik yasaları yaklaşık bu uzaya bir determinant-1 birimsel dönüşümü uygulaması altında değişmezdir :[2]
Örneğin, açacak tüm yukarı kuarklar evrensel içindedir aşağı kuarklar içinde ve tam tersi. Bazı örnekler bu dönüşümlerin olası etkilerini netleştirmeye yardımcı:
- Bu birimsel dönüşümler bir protona uygulanıyor ise, o bir nötron içinde dönüştürülebilir, veya Bir proton ve nötronun bir süperpozisyon içerisine, ama başka parçacıklar halinde.Bunun için, kuantum durumunun bir iki-boyutlu uzay dönüşümleri etrafında hareket eden proton.Proton ve nötron bir "izospin çiftli" denir, bir spin ½ parçacık davranışı altında matematiksel analogu sıradan dönmedir.
- Bu birimsel dönüşüm ise üç pionun herhangi uygulamasıdır (Pion0,Pion+, ve Pion-),Bu herhangi diğer pionların herhangi değişikliği olabilir,ama herhangi olmayan parçacığın içine değil. Bunun için, kuantum durumlarının bir üç-boyutlu uzay çevresinde taşınan dönüşümlerdir.Pionlara bir "izospin üçlüsü" denir, bir spin 1 parçacıkların davranışı altında düzgün dönmeye matematiksel analog denir
- Bu dönüşümlerin bir elektron üzerinde hiçbir etkisi yoktur , çünkü bu hiçbiri ne de bir yukarı kuarklar içerir.Elektron bir izospin tekli denir, bir spin 0 parçacıklar davranışlar altında böyle düzgün dönme matematiksel analoglar.
Genelde, izospin çoklusu formunda parçacıklar, Lie cebiri SU(2)nin gösterimi indirgenememeye karşı gelir. Bir izospin içindeki parçacıklar nedeniyle yukarı ve aşağı kuarklar, çok benzeyen ama aynı olmayan kütlelere sahiptirler çok benzer özdeş ama çoklu değildirler
Örnekler: Çeşni simetri
Izospin simetri çeşni simetriye genelleştirilebilir, bir SU(3) grup yukarı kuarklar arasında benzerliğe karşılık gelir, aşağı kuarklar, ve garip kuarklar.[2] Bu, yine, bir yaklaşık simetridir, farklı kütleli kuarklar tarafından ihlal edilir ve elektrozayıf etkileşimler—aslında, bu bir izospinden kötü bir yaklaşıklıktır, çünkü garip kuarkın belirgin daha yüksek kitlesi vardır.
Yine de, parçacık Lie cebiri SU(3)nin indirgenemeyen gösterim grubu içine gerçekten de özenle ayrılabilir ,ilk olarak Murray Gell-Mann ile notedildi ve Yuval Ne'eman ile bağımsızlaştırıldı (bkzsekiz misli yol).
Ayrıca bakınız
- Lie cebiri
- Lie grupları
- Poincaré grubu
- Gösterim teorisi:
- Lie cebirinin
- Lie gruplarının
- Poincaré gruplarının
- özel birimsel grup
- Simetri
Kaynakça
- Coleman, Sidney (1985) Aspects of Symmetry: Selected Erice Lectures of Sidney Coleman. Cambridge Univ. Press. ISBN 0-521-26706-4.
- Georgi, Howard (1999) Lie Algebras in Particle Physics. Reading, MA: Perseus Books. ISBN 0-7382-0233-9.
- Hall, Brian C., (2006) Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. Springer. ISBN 0-387-40122-9.
- Sternberg, Shlomo (1994) Group Theory and Physics. Cambridge Univ. Press. ISBN 0-521-24870-1. Especially pp. 148–150.
- Steven Weinberg (1995). The Quantum Theory of Fields, Volume 1: Foundations. Cambridge Univ. Press. ISBN 0-521-55001-7. Especially appendices A and B to Chapter 2.
Notlar
- See Weinberg (1995), Chapter 2 appendix A and B.
- "Lecture notes by Prof. Mark Thomson" (PDF). 5 Temmuz 2016 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 14 Mart 2014.