Sayısal türev

Sayısal analizde, fonksiyonun değerleri veya fonksiyon hakkında bilinen diğer bilgiler kullanılarak bir matematiksel fonksiyonun türevinin hesaplanmasında kullanılan algoritmalara sayısal türev denir.

sayısal türev kesen doğru grafiği

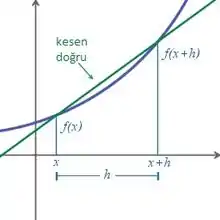
Sonlu farklar formülü

En basit yöntem sonlu fark yaklaşımı kullanmaktadır. (x,f(x)) ve (x+h,f(x+h))[1] noktalarından geçen kesen doğru civarındaki eğimin hesaplanması için basit bir iki nokta tahmini yapılır. x'teki değişikliği ifade eden küçük bir h sayısı seçilir, bu sayı negatif veya pozitif olabilir.

Bu çizginin eğimi şu şekilde tanımlanır:

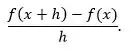
Buna Newton'un bölünmüş fark formülü denir.

Kesen doğrunun eğimi teğet doğrusunun eğiminden farklıdır ve bu fark yaklaşık olarak h sayısına eşittir. h sayısı sıfıra yaklaşırken kesen doğrunun eğimi, teğet doğrusunun eğimine yaklaşır. Bu yüzden, tıpkı kesen doğrularının birbirine yaklaşarak teğet doğrusu oluşturması gibi f'in x'teki türevi bölünmüş farkın limit değeridir:

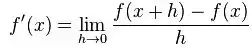
h yerine 0 konulmasıyla elde edilen sonuçta paydada 0 olduğundan türevin direkt hesaplanması mantıksız olabilir. Aynı şekilde, eğim (x-h) ve x noktaları kullanılarak da bulunabilir.Kesen doğrunun civarındaki eğimin hesaplanması için (x-h,f(x-h)) ve (x+h,f(x+h)) noktalarının kullanıldığı bir başka iki nokta formülü:

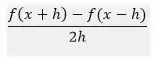
Bu durumda birinci dereceden hatalar iptal olur, bu nedenle kesen doğrunun eğimi h^2 ile orantılı olarak teğet doğrusunun eğiminden farklıdır. Bu yüzden h sayısının küçük değerlerinde teğet doğrusu için bu yaklaşım tek taraflı yaklaşımdan daha kesin bir sonuç vermektedir. Bu teoremde x noktasındaki eğim hesaplanmasına rağmen fonksiyonun x noktasındaki değerine gerek duyulmaz. Bu yöntemle bulunan eğim de bir hata payı içerir ve bu hata payını veren formül:

formüldeki “c” değeri “x-h” ve “x+h” noktaları arasında bir değerdir. Bu hata, hesaplamaların sınırlı hassaslıkla yapılmasından ve sayıların gösteriminden kaynaklanan yuvarlama hatasını içermez.

Yüksek mertebe yöntemleri

Türev hesaplamalarında kullanılan ve daha kesin sonuçlar veren yüksek mertebeden yöntemler olduğu gibi daha yüksek mertebeden türevlerin hesaplanması için yöntemler mevcuttur. Sayısal türev hesaplamalarında daha fazla nokta kullanılarak yapılan yaklaşımlarda daha iyi sonuçlar elde edilmektedir. Üç ve beş nokta üzerinden yapılan hesaplamalar daha yaygın olarak kullanılır[2].

Üç nokta formülleri

Beş nokta formülleri

Kaynakça
  1. Richard L. Burden, J. Douglas Faires (2000), Numerical Analysis, (7th Ed), Brooks/Cole. ISBN 0-534-38216-9
  2. Abramowitz & Stegun, Table 25.2
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.