Silindirik ve küresel koordinatlarda vektör alanı

NOT: Bu sayfa küresel koordinatların fizik gösterimi içindir, ${\displaystyle \theta }$ z ekseni arasındaki açıdır.ve yarıçap vektörü söz konusu noktaya orijinden bağlantılıdır , bu ${\displaystyle \phi }$ açısı x-y düzlemi ve x ekseni ile vektör yarıçapının izdüşümü arası açıdır. Diğer bazı tanımları da kullanılıyor ve çok dikkatli farklı kaynaklardan karşılaştırarak alınmalıdır.[1]

Küresel koordinatlar (r, θ, φ) fizikte ortak kullanılır: yarıçap uzunluğu r, kutupsal açı θ (teta), ve azimut açı φ (phi). ρ (rho) sembolü ise r vektörünün xy düzlemindeki izdüşüm vektörüdür.Yaygın kullanım bu şekildedir.

Silindirik koordinat sistemi

Vektör alanı

Vektörler (p,  φ, z) ile silindirik koordinatlarda tanımlanıyor , burada

• p , xy düzlemine r vektörünün izdüşüm uzunluğu ,
•  φ pozitif x-ekseninin (0 ≤  φ < 2π) xy-düzlemi (i.e. r)vektör izdüşümünü ile arasındaki açıdır,
• z bilinen z-koordinatı.

(p, φ, z) kartezyen koordinat'larda şöyle verilir.:

${\textstyle {\begin{bmatrix}p\\\phi \\z\end{bmatrix}}={\begin{bmatrix}{\sqrt {x^{2}+y^{2}}}\\\operatorname {arctan} (y/x)\\z\end{bmatrix}},\ \ \ 0\leq \phi <2\pi ,}$

veya tersi yoluyla:

${\displaystyle {\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}p\cos \phi \\p\sin \phi \\z\end{bmatrix}}.}$

Herhangi bir vektör alanı birim vektörleri tarafından yazılabilir:

${\displaystyle \mathbf {A} =A_{x}\mathbf {\hat {x}} +A_{y}\mathbf {\hat {y}} +A_{z}\mathbf {\hat {z}} =A_{p}\mathbf {\hat {p}} +A_{\phi }{\boldsymbol {\hat {\phi }}}+A_{z}\mathbf {\hat {z}} }$

Silindirik birim vektörleri ile kartezyen birim vektörleri ilişkilidir:

${\displaystyle {\begin{bmatrix}\mathbf {\hat {p}} \\{\boldsymbol {\hat {\phi }}}\\\mathbf {\hat {z}} \end{bmatrix}}={\begin{bmatrix}\cos \phi &\sin \phi &0\\-\sin \phi &\cos \phi &0\\0&0&1\end{bmatrix}}{\begin{bmatrix}\mathbf {\hat {x}} \\\mathbf {\hat {y}} \\\mathbf {\hat {z}} \end{bmatrix}}}$

• Not: bu matris bir ortogonal matristir,şöyle ki ,o terstir, basittir,transpozedir.

Bir vektör alanının zaman türevleri

"vektör alanı A"nın zaman içindeki değişikliklerini bulmak için biz zaman türevlerini hesaplıyoruz.

Bunu desteklemek için zaman türevleri için biz Newton gösterimini kullanıyoruz (${\displaystyle {\dot {\mathbf {A} }}}$). Kartezyen koordinatlar içinde bu basitçe:

${\displaystyle {\dot {\mathbf {A} }}={\dot {A}}_{x}{\hat {\mathbf {x} }}+{\dot {A}}_{y}{\hat {\mathbf {y} }}+{\dot {A}}_{z}{\hat {\mathbf {z} }}}$

Bununla birlikte silindirik koordinatlar şu alınır:

${\displaystyle {\dot {\mathbf {A} }}={\dot {A}}_{p}{\hat {\boldsymbol {p}}}+A_{p}{\dot {\hat {\boldsymbol {p}}}}+{\dot {A}}_{\phi }{\hat {\boldsymbol {\phi }}}+A_{\phi }{\dot {\hat {\boldsymbol {\phi }}}}+{\dot {A}}_{z}{\hat {\boldsymbol {z}}}+A_{z}{\dot {\hat {\boldsymbol {z}}}}}$

Birim vektörlerin zaman türevlerine ihtiyacımız var.

${\displaystyle {\begin{aligned}{\dot {\hat {\mathbf {p} }}}&={\dot {\phi }}{\hat {\boldsymbol {\phi }}}\\{\dot {\hat {\boldsymbol {\phi }}}}&=-{\dot {\phi }}{\hat {\mathbf {p} }}\\{\dot {\hat {\mathbf {z} }}}&=0\end{aligned}}}$

ile verilir. Zaman türevleri basitçe:

${\displaystyle {\dot {\mathbf {A} }}={\hat {\boldsymbol {p}}}({\dot {A}}_{p}-A_{\phi }{\dot {\phi }})+{\hat {\boldsymbol {\phi }}}({\dot {A}}_{\phi }+A_{p}{\dot {\phi }})+{\hat {\mathbf {z} }}{\dot {A}}_{z}}$

Bir vektör alanın ikinci kez türevi

fizik'te ilginç olan ikinci zaman türevidir, klasik mekanik sistemde hareketin denklemi bulunuyor . Bir vektör alanının silindirik koordinatlarda ikinci zaman türevi şu denklem yoluyla veriliyor:

${\displaystyle \mathbf {\ddot {A}} =\mathbf {\hat {p}} ({\ddot {A}}_{p}-A_{\phi }{\ddot {\phi }}-2{\dot {A}}_{\phi }{\dot {\phi }}-A_{p}{\dot {\phi }}^{2})+{\boldsymbol {\hat {\theta }}}({\ddot {A}}_{\phi }+A_{p}{\ddot {\phi }}+2{\dot {A}}_{p}{\dot {\phi }}-A_{\phi }{\dot {\phi }}^{2})+\mathbf {\hat {z}} {\ddot {A}}_{z}}$

Bu ifadeyi anlamak için, A = P eşitliğine inanıyoruz, burada p, (r, θ, z) vektörüdür.

Bu demektir ki ${\displaystyle \mathbf {A} =\mathbf {P} =p\mathbf {\hat {p}} +z\mathbf {\hat {z}} }$.

Biz koymak yerine sonra:

${\displaystyle {\ddot {\mathbf {P} }}=\mathbf {\hat {p}} ({\ddot {p}}-p{\dot {\phi }}^{2})+{\boldsymbol {\hat {\phi }}}(p{\ddot {\phi }}+2{\dot {p}}{\dot {\phi }})+\mathbf {\hat {z}} {\ddot {z}}}$

Mekanikte,bu şekilde ifade açısından:

${\displaystyle {\begin{aligned}{\ddot {p}}\mathbf {\hat {p}} &={\mbox{central outward acceleration}}\\-p{\dot {\phi }}^{2}\mathbf {\hat {p}} &={\mbox{centripetal acceleration}}\\p{\ddot {\phi }}{\boldsymbol {\hat {\phi }}}&={\mbox{angular acceleration}}\\2{\dot {p}}{\dot {\phi }}{\boldsymbol {\hat {\phi }}}&={\mbox{Coriolis effect}}\\{\ddot {z}}\mathbf {\hat {z}} &={\mbox{z-acceleration}}\end{aligned}}}$

Ayrıca bakınız: merkezcil çekim kuvveti, Açısal hız, Coriolis etkisi.

Küresel koordinat sistemi

Vektör alanı

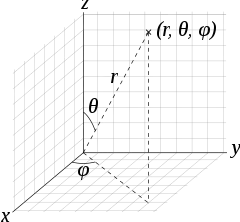
(r,θ,φ) ile küresel koordinatlar içinde tanımlanan vektörler

• r vektörünün boyudur,
• θ pozitif z-ekseni ve söz konusu vektör arasındaki açı(0 ≤ θ ≤ π)
• φ vektör ontolojik "X-Y" düzleminin projeksiyonu ve x-ekseni pozitif tarafı arasındaki açıdır(0 ≤ φ < 2π),

(by:

${\displaystyle {\begin{bmatrix}\ r\\\theta \\\phi \end{bmatrix}}={\begin{bmatrix}{\sqrt {x^{2}+y^{2}+z^{2}}}\\\arccos(z/\ r)\\\arctan(y/x)\end{bmatrix}},\ \ \ 0\leq \theta \leq \pi ,\ \ \ 0\leq \phi <2\pi ,}$

tarafından

ya da ters tarafından:

${\displaystyle {\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}\ r\sin \theta \cos \phi \\\ r\sin \theta \sin \phi \\\ r\cos \theta \end{bmatrix}}.}$

Birim vektör yardımıyla herhangi bir vektör alanı yazılabilir:

${\displaystyle \mathbf {A} =A_{x}\mathbf {\hat {x}} +A_{y}\mathbf {\hat {y}} +A_{z}\mathbf {\hat {z}} =A_{r}{\boldsymbol {\hat {r}}}+A_{\theta }{\boldsymbol {\hat {\theta }}}+A_{\phi }{\boldsymbol {\hat {\phi }}}}$

Küresel birim vektör are Kartezyen birim vektörlerle şöyle ilişkilidir:

${\displaystyle {\begin{bmatrix}{\boldsymbol {\hat {r}}}\\{\boldsymbol {\hat {\theta }}}\\{\boldsymbol {\hat {\phi }}}\end{bmatrix}}={\begin{bmatrix}\sin \theta \cos \phi &\sin \theta \sin \phi &\cos \theta \\\cos \theta \cos \phi &\cos \theta \sin \phi &-\sin \theta \\-\sin \phi &\cos \phi &0\end{bmatrix}}{\begin{bmatrix}\mathbf {\hat {x}} \\\mathbf {\hat {y}} \\\mathbf {\hat {z}} \end{bmatrix}}}$

• Not: Bu matris bir ortogonal matristir, o terstir, basitçetranspozedir.

Bir vektör alanın zaman türevi

Zaman içinde nasıl vektör alanı bir değişiklik bulmak için biz zaman türevinin hesaplamalıyız Kartezyen koordinatlarda bu basitçe:

${\displaystyle \mathbf {\dot {A}} ={\dot {A}}_{x}\mathbf {\hat {x}} +{\dot {A}}_{y}\mathbf {\hat {y}} +{\dot {A}}_{z}\mathbf {\hat {z}} }$

Ancak, küresel koordinatlarda Bu hale gelir:

${\displaystyle \mathbf {\dot {A}} ={\dot {A}}_{r}{\boldsymbol {\hat {r}}}+A_{r}{\boldsymbol {\dot {\hat {r}}}}+{\dot {A}}_{\theta }{\boldsymbol {\hat {\theta }}}+A_{\theta }{\boldsymbol {\dot {\hat {\theta }}}}+{\dot {A}}_{\phi }{\boldsymbol {\hat {\phi }}}+A_{\phi }{\boldsymbol {\dot {\hat {\phi }}}}}$

Bu birim vektörlerin zaman türevleri gerekir. Bunlar tarafından verilmektedir:

${\displaystyle {\begin{aligned}{\boldsymbol {\dot {\hat {r}}}}&={\dot {\theta }}{\boldsymbol {\hat {\theta }}}+{\dot {\phi }}\sin \theta {\boldsymbol {\hat {\phi }}}\\{\boldsymbol {\dot {\hat {\theta }}}}&=-{\dot {\theta }}{\boldsymbol {\hat {r}}}+{\dot {\phi }}\cos \theta {\boldsymbol {\hat {\phi }}}\\{\boldsymbol {\dot {\hat {\phi }}}}&=-{\dot {\phi }}\sin \theta {\boldsymbol {\hat {r}}}-{\dot {\phi }}\cos \theta {\boldsymbol {\hat {\theta }}}\end{aligned}}}$

zamana göre türevleri alınırsa:

${\displaystyle \mathbf {\dot {A}} ={\boldsymbol {\hat {r}}}({\dot {A}}_{r}-A_{\theta }{\dot {\theta }}-A_{\phi }{\dot {\phi }}\sin \theta )+{\boldsymbol {\hat {\theta }}}({\dot {A}}_{\theta }+A_{r}{\dot {\theta }}-A_{\phi }{\dot {\phi }}\cos \theta )+{\boldsymbol {\hat {\phi }}}({\dot {A}}_{\phi }+A_{r}{\dot {\phi }}\sin \theta +A_{\theta }{\dot {\phi }}\cos \theta )}$

Ayrıca bakınız

• gradyan, diverjans, curl özellikleri için, Silindirik ve küresel koordinatlarda del ve laplasyen in çeşitli koordinat sistemlerinde.

kaynakça

1. "Wolfram Mathworld, spherical coordinates". 5 Ekim 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ekim 2013.