İşaret (matematik)
Matematikte işaret kavramı, sıfırdan farklı her bir reel sayının pozitif veya negatif olduğunu belirtir. Her ne kadar bazen işaretli sıfır kullanılsa bile, sıfırın kendisi işaretsizdir. Matematik ve fizikte kullanılan reel sayıların toplamaya göre tersini (−1 ile çarpma) ifade etmek için işaret değiştirme işlemi yapılır.

Bir sayının işareti
Eğer bir reel sayı sıfırdan büyük ise pozitif, sıfırdan küçük ise negatif olarak adlandırılır. Pozitif veya negatif olma özelliği, sayının işareti olarak adlandırılır. Her ne kadar argümanda işaret bulunsa bile, işaretler karmaşık sayılarda tanımlı değildir.
Aritmetik ve diğer yerlerde kullanılan çoğu sayısal gösterimde bir sayının işaretini belirtmek için, sayının önüne artı işareti veya eksi işareti konulur. Örneğin +3, 3'ün pozitif olduğunu; -3 ise 3'ün negatif olduğunu ifade eder. Eğer sayıda artı veya eksi işareti bulunmuyorsa, bu sayı pozitiftir. Eksi işareti daha çok çıkarmayı ifade eder. Cebirde artı işareti, çoğunlukla toplamaya göre ters (bazen negasyon olarak adlandırılır) işlemini ifade eder. Pozitif bir sayının toplamaya göre tersi, negatif sayıyı; negatif bir sayının toplamaya göre tersi de pozitif sayıyı verir. Örneğin −(−3) = +3'dür.
Mutlak değer fonksiyonu kullanılarak sıfırdan farklı herhangi bir sayı, pozitif yapılabilir. Örneğin hem -3 hem de 3 sayılarının mutlak değeri 3'dür. Sembolik olarak şöyle yazılır: |−3| = 3 ve |3| = 3.
Sıfırın işareti
0 sayısı, ne pozitif ne de negatiftir. Bu yüzden işaretsizdir. Aritmetikte kullanılan +0 ve −0'nın her ikisi de, toplamaya göre tersi kendisi olan 0 ifade eder.
Bilişimdeki işaretli sayı temsilleri gibi bazı uygulamalarda, işaretli sıfır kullanılır. Burada pozitif sıfır ile negatif sıfır farklı sayıları ifade eder.
Kalkülüs ve matematiksel analizde tek taraflı limitleri hesaplamak için +0 ve −0 kullanılır. Bu gösterim, bir fonksiyonun giriş değişkeninin sırasıyla pozitiften veya negatiften 0'a yaklaşmasının belirtir. Bu yaklaşımın aynı olması gerekmez.
İşaretlerin terminolojisi
Sıfır, ne pozitif ne de negatif olmadığından dolayı (çoğu ülkelerde), bilinmeyen bir sayının işaretinin belirtmek için aşağıdaki terminolojiler kullanılır:
- Eğer sayı sıfırdan büyük ise, pozitiftir.
- Eğer sayı sıfırdan küçük ise, negatiftir.
- Eğer sayı sıfıra büyük eşit ise, negatif değildir.
- Eğer sayı sıfıra küçük eşit ise, pozitif değildir.
Negatif olmayan bir sayı, ya pozitiftir ya da sıfırdır. Benzer şekilde pozitif olmayan bir sayı, ya negatiftir ya da sıfırdır. Örneğin; bir reel sayının mutlak değeri, hiçbir zaman negatif değildir. Fakat pozitif olması da gerekmez.
Aynı terminoloji bazen reel ya da tam sayılı fonksiyonlar için de kullanılır. Örneğin; eğer bir fonksiyonun tüm değerleri pozitif ise, "fonksiyon pozitiftir"; tüm değerleri negatif ise, "fonksiyon negatiftir" denir.
İşaret fonksiyonu
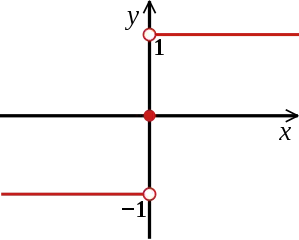
İşaret fonksiyonu veya signum fonksiyonu, bazen bir sayının işaretini çıkartmak için kullanılır. Bu fonksiyon genellikle şöyle tanımlanır:
Eğer x pozitif ise, sgn(x), 1; x negatif ise, sgn(x), −1'dir. Sıfır olmayan x değerleri için, bu fonksiyon şu formülle gösterilir:
burada |x|, x in mutlak değeridir.
İşaretin anlamı
Açının işareti
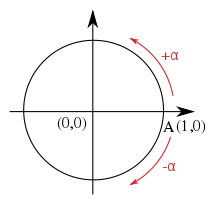
Özellikle yönlü açı veya bir açının dönüşünün ölçüsünü belirtmek için çoğunlukla bir işaret kullanılır. Çoğunlukla açı saat yönünde olduğunda işaret kullanılır. Her ne kadar farklı kullanımlar olsa bile matematikte genellikle saat yönündeki açılar negatif, saat yönünün tersindeki açılar pozitif olarak kabul edilir.
Bir açının yönünü üç boyutlu olarak belirlemek için, sabit bir eksen etrafında dönüş yaptığı varsayılarak, açı işaretlenir. Özellikle, yönlü eksen etrafında sağ el dönüşü, pozitif olarak hesaplanırken, sol el dönüşü negatif olarak hesaplanır.
Değişimin işareti
x miktarı zamanla değiştiğinde, x değerindeki değişim, genellikle şu denklemle ifade edilir.
Bu dönüşümde, x miktarındaki artmaya "pozitif değişim", x miktarındaki azalmaya "negatif değişim" denir. Kalkülüste aynı dönüşüm türevi ifade etmek için kullanılır. Sonuç olarak herhangi bir artan fonksiyonu pozitif türevli iken, azalan fonksiyon negatif türevlidir.
Yönün işareti
Analitik geometri ve fizikte, genellikle kartezyen yönünü pozitif veya negatif olarak belirlemektir. Örneğin, sayı doğrusunda, pozitif sayılar sağa, negatif sayılar ise sola yazılır:
Doğrusal hareket, yerdeğişimi veya hızdan sağ, genellikle pozitif, sol da negatif olarak düşünülür.
Kartezyen koordinat sisteminde sağ taraf, genellikle pozitif x yönü; üst taraf genellikle, pozitif y yönüdür. Eğer bir yerdeğişimi veya hız vektörünün bileşenleri ayrı ise, yatay bileşenin sağa doğru hareket eden kısım pozitif, sola doğru hareket eden kısmı negatiftir. Düşey bileşenin yukarı doğru hareket eden kısmı pozitif, aşağı doğru hareket eden kısmı negatiftir.
Bilişimde işaretlilik
| yüksek öncelikli bit | |||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | 127 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | 126 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | = | 2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | −1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | −2 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | −127 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | −128 |
Şablon:Caption
Bilişimde tam sayı değeri, bilgisayarın bir işaretin iz sayısını tutmasına bağlı olarak ya işaretli ya da işaretsiz olabilir. Bir tam sayı değişkeni yalnızca negatif olmayan değerlerle kısıtlandırılarak, bir sayının değerini tutmak için bir bit daha kullanılabilir. Çünkü bilgisayarla yapılır tam sayı aritmetik yönteminde, bir işaretli tam sayı değişkeninin işareti, genellikle tek bağımlı bit olarak tutulmaz. Bunun için, ikinin tümleyeni veya diğer bazı işaretli sayı temsili kullanılarak tutulur.