Brahmagupta teoremi

Geometride, Brahmagupta teoremi, eğer bir kirişler dörtgeni ortodiyagonal ise (yani, dik köşegenlere sahipse), o zaman köşegenlerin kesişme noktasından bir kenara çizilen dikmenin karşı kenarı daima ikiye böldüğünü belirtir.[1] Adını Hint matematikçi Brahmagupta'dan (598-668) almıştır.[2]

${\displaystyle {\overline {BD}}\perp {\overline {AC}},{\overline {EF}}\perp {\overline {BC}}}$${\displaystyle \Rightarrow |{\overline {AF}}|=|{\overline {FD}}|}$

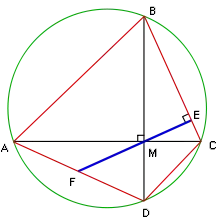
Teoremin açıklaması

Daha spesifik olarak, ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ ve ${\displaystyle D}$, ${\displaystyle AC}$ ve ${\displaystyle BD}$ doğrularının dik olacağı şekilde bir daire üzerinde dört nokta olsun. ${\displaystyle AC}$ ve ${\displaystyle BD}$'nin kesişme noktasını ${\displaystyle M}$ ile gösterilsin. ${\displaystyle M}$'den ${\displaystyle BC}$ doğrusuna dik çizilsin ve ${\displaystyle E}$ kesişme noktasına gelsin. ${\displaystyle F}$, ${\displaystyle EM}$ doğrusu ile ${\displaystyle AD}$ kenarının kesişim noktası olsun. Daha sonra teorem, ${\displaystyle F}$'nin ${\displaystyle AD}$ doğru parçasının orta noktası olduğunu belirtir.

Teoremin ispatı

Teoremin kanıtı.

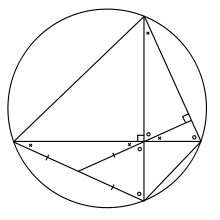
${\displaystyle AF=FD}$ olduğunu kanıtlamamız gerekiyor. Biz ${\displaystyle AF}$ ve ${\displaystyle FD}$'nin aslında ${\displaystyle FM}$'ye eşit olduklarını ispat edeceğiz.

${\displaystyle AF=FM}$ olduğunu kanıtlamak için, önce ${\displaystyle \angle FAM}$ ve ${\displaystyle \angle CBM}$ açılarının eşit olduğuna dikkat edin, çünkü bunlar dairenin aynı yayını gören çevre açılardır. Ayrıca, ${\displaystyle \angle CBM}$ ve ${\displaystyle \angle CME}$ açılarının her ikisi de ${\displaystyle \angle BCM}$ açısına tamamlayıcıdır (yani toplamları 90°'ye eşittir) ve bu nedenle her iki açı eşittirler. Son olarak, ${\displaystyle \angle CME}$ ve ${\displaystyle \angle FMA}$ açıları aynıdır. Dolayısıyla, ${\displaystyle \triangle AFM}$ bir ikizkenar üçgendir ve dolayısıyla ${\displaystyle AF}$ ve ${\displaystyle FM}$ kenarları eşittir.

${\displaystyle FD=FM}$'nin benzer şekilde gittiğinin kanıtı: ${\displaystyle \angle FDM}$, ${\displaystyle \angle BCM}$, ${\displaystyle \angle BME}$ ve ${\displaystyle \angle DMF}$ açılarının tümü eşittir, bu nedenle ${\displaystyle \triangle DFM}$ bir ikizkenar üçgendir, dolayısıyla ${\displaystyle FD=FM}$'dir. Buradan teoremin iddia ettiği gibi ${\displaystyle AF=FD}$ olduğu görülebilir.

Ayrıca bakınız

• Kirişler dörtgeninin alanı için Brahmagupta formülü

Kaynakça

1. Bradley, Michael (2006). The birth of mathematics : ancient times to 1300. New York: Infobase Publishing. ss. 70, 85. ISBN 0-8160-5423-1. OCLC 62152830.
2. Coxeter, H. S. M.; Greitzer, Samuel L. (1967). Geometry Revisited (PDF). 19. Washington, DC: Math. Assoc. Amer. s. 59. ISBN 0-88385-619-0.

Dış bağlantılar ve ilave okumalar

• Brahmagupta teoremi @ Proofwiki
• Brahmagupta Teoremi @ cut-the-knot
• Eric W. Weisstein, Brahmagupta's theorem (MathWorld)
• Murthy, M. N. (2019). Brahmagupta’s theorem. At Right Angles, (5), 27.
• Kaye, G. R. (1919). Indian mathematics. Isis, 2(2), ss. 326-356.
• Dvorožňák, Marek & Pech, Pavel. (2009), Brahmagupta’s Theorem Automatic Computer Proof
• Askey R. (2010) Completing Brahmagupta’s Extension of Ptolemy’s Theorem. In: Alladi K., Klauder J., Rao C. (eds) The Legacy of Alladi Ramakrishnan in the Mathematical Sciences. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-6263-8_11
• Dashrath Kumar & Dr. Mrityunjay JhaA, (2019), Critical Study of Brahmagupta’s Theorems on Cyclic Quadrilateral, JETIR, March 2019, Volume 6, Issue 3, ISSN 2349-5162, ss. 383-384
• Richeson, A. (1930). An Extension of Brahmagupta's Theorem. American Journal of Mathematics, 52(2), ss. 425-438. doi:10.2307/2370695