Brahmagupta formülü

Öklid geometrisinde, Brahmagupta formülü, kenarların uzunlukları göz önüne alındığında herhangi bir kirişler dörtgeninin (daire içine çizilebilen dörtgen) alanını bulmak için kullanılır.

Formül

Brahmagupta formülü, kenarlarının uzunluğu a, b, c, d olan bir kirişler dörtgeninin K alanını aşağıdaki şekilde verir:

${\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}}$

burada s, yarı çevre olarak aşağıdaki şekilde tanımlanır;

${\displaystyle s={\frac {a+b+c+d}{2}}.}$

Bu formül, bir üçgenin alanını hesaplamak için verilen için Heron formülünü genelleştirir. Bir üçgen, bir kenarı sıfır olan bir dörtgen olarak kabul edilebilir. Bu perspektiften, d sıfıra yaklaştıkça, bir kirişler dörtgeni, çember içine çizilen bir üçgene yakınsar (tüm üçgenler çember içine çizilebilir) ve Brahmagupta formülü, Heron formülüne sadeleştirilir.

Yarı çevre kullanılmazsa, Brahmagupta formülü aşağıdaki şekilde yazılır:

${\displaystyle K={\frac {1}{4}}{\sqrt {(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}}.}$

Başka bir eşdeğer versiyon da aşağıdaki gibidir:

${\displaystyle K={\frac {\sqrt {(a^{2}+b^{2}+c^{2}+d^{2})^{2}+8abcd-2(a^{4}+b^{4}+c^{4}+d^{4})}}{4}}\cdot }$

İspat

İspat için referans çizim

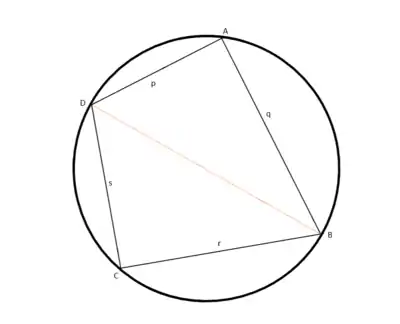
Trigonometrik ispat

Burada sağdaki şekildeki gösterimler kullanılmıştır. Kirişler dörtgeninin K alanı, △ADB ve △BDC alanlarının toplamına eşittir:

${\displaystyle ={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin C.}$

Ancak ABCD bir kirişler dörtgeni olduğundan, ∠DAB = 180° − ∠DCB. Dolayısıyla, sin A = sin C 'dir. Bu nedenle,

${\displaystyle K={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin A}$

${\displaystyle K^{2}={\frac {1}{4}}(pq+rs)^{2}\sin ^{2}A}$

${\displaystyle 4K^{2}=(pq+rs)^{2}(1-\cos ^{2}A)}$

Ortak kenar DB için çözülürse, △ADB ve △BDC üçgenlerinde Kosinüs yasası aşağıdaki özdeşliği verir:

${\displaystyle p^{2}+q^{2}-2pq\cos A=r^{2}+s^{2}-2rs\cos C.}$

cos C = −cos A (A ve C açıları bütünler açı olduğu için) yerine konur ve eşitlik yeniden düzenlenirse aşağıdaki ifade elde edilir;

${\displaystyle 2(pq+rs)\cos A=p^{2}+q^{2}-r^{2}-s^{2}.}$

Bunu alan denkleminde yerine yazarsak,

${\displaystyle 4K^{2}=(pq+rs)^{2}-{\frac {1}{4}}(p^{2}+q^{2}-r^{2}-s^{2})^{2}}$

${\displaystyle 16K^{2}=4(pq+rs)^{2}-(p^{2}+q^{2}-r^{2}-s^{2})^{2}.}$

Sağ taraf a² − b² = (a − b)(a + b) biçimindedir ve bu nedenle şu şekilde yazılabilir:

${\displaystyle [2(pq+rs)-p^{2}-q^{2}+r^{2}+s^{2}][2(pq+rs)+p^{2}+q^{2}-r^{2}-s^{2}]}$

köşeli parantez içindeki terimleri yeniden düzenledikten sonra,

${\displaystyle =[(r+s)^{2}-(p-q)^{2}][(p+q)^{2}-(r-s)^{2}]}$

${\displaystyle =(q+r+s-p)(p+r+s-q)(p+q+s-r)(p+q+r-s).}$

Yarı çevre S = p + q + r + s2 olarak dikkate alınırsa,

${\displaystyle 16K^{2}=16(S-p)(S-q)(S-r)(S-s).}$

Her iki tarafın karekökünü alırsak,

${\displaystyle K={\sqrt {(S-p)(S-q)(S-r)(S-s)}}.}$

elde edilir.

Trigonometrik olmayan ispat

Brahmagupta Formülünün ispatı için kullanılacak şekil

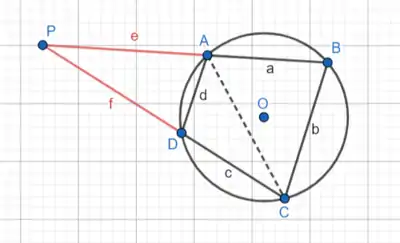
Trigonometrik olmayan alternatif bir kanıt, Heron'un üçgen alan formülünün benzer üçgenler üzerindeki iki uygulamasını kullanır.[1]

Kirişler dörtgenine ${\displaystyle AC}$ kirişini çizelim. ${\displaystyle AB}$ ve ${\displaystyle CD}$ doğru parçasını uzatalım, böylece ${\displaystyle P}$ noktasında kesişsinler.

${\displaystyle \angle ADC}$ ve ${\displaystyle \angle ABC}$ açıları, çemberin iki yayından aynı ${\displaystyle AC}$ kirişini görür. Bu nedenle bütünler açılardır. ${\displaystyle \angle ADP}$, ${\displaystyle \angle ADC}$'nin bütünleyicisidir. Yani ${\displaystyle \angle ADP\cong \angle ABC}$'dir. ${\displaystyle \triangle PBC}$ ve ${\displaystyle \triangle PDA}$ benzerdir. Benzerlik oranı ise ${\displaystyle {\frac {d}{b}}}$'dir.

${\displaystyle {Alan}(\triangle PDA)={\frac {d^{2}}{b^{2}}}{Alan}(\triangle PBC)}$

${\displaystyle {Alan}(ABCDA)={Alan}(\triangle PBC)-{Alan}(\triangle PDA)}$

${\displaystyle ABCD}$ dörtgeninin alanına A ve ${\displaystyle \triangle PBC}$ üçgeninin alanına da T diyelim.

${\displaystyle A=T-{\frac {d^{2}}{b^{2}}}T=(1-{\frac {d^{2}}{b^{2}}})T={\frac {(b^{2}-d^{2})}{b^{2}}}T}$

${\displaystyle PA=e}$ ve ${\displaystyle PD=f}$ olarak alınarak Heron formülü uygulanırsa, ${\displaystyle {Alan}(\triangle PBC)}$ aşağıdaki şekilde bulunur:

${\displaystyle T={\sqrt {s(s-(e+a))(s-(f+c))(s-b)}}}$

${\displaystyle s={\frac {e+a+f+c+b}{2}}}$

Bu nedenle,

${\displaystyle A={\frac {(b^{2}-d^{2})}{b^{2}}}{\sqrt {s(s-(e+a))(s-(f+c))(s-b)}}}$

(Not: Bu noktada ÜÇGEN'in yarı çevresi için s kullandık. Aşağıda, s, e ve f için a, b, c ve d cinsinden terimleri yerine koyacağız. Sonunda dörtgenin yarı çevresini temsil eden s kullanıma geri döneceğiz.)

• İlk olarak, e’yi a, b, c ve d cinsinden ifade etmek istiyoruz.

${\displaystyle {\frac {e+a}{b}}={\frac {f}{d}}}$

${\displaystyle e={\frac {fb}{d}}-a}$

${\displaystyle ed+ad=fb}$

${\displaystyle ed+ad=({\frac {eb}{d}}-c)b}$

${\displaystyle ed+ad={\frac {eb^{2}}{d}}-cb}$

${\displaystyle ed+ad={\frac {eb^{2}-cbd}{d}}}$

${\displaystyle ed^{2}+ad^{2}=eb^{2}-cbd}$

${\displaystyle ed^{2}-eb^{2}=-(ad^{2}+cbd)}$

${\displaystyle e(d^{2}-b^{2})=-d(ad+cb)}$

${\displaystyle e={\frac {-d(ad+cb)}{d^{2}-b^{2}}}}$ veya

${\displaystyle e={\frac {d(ad+cb)}{b^{2}-d^{2}}}}$

• Sonra, f’yi a, b, c ve d cinsinden ifade etmek istiyoruz.

${\displaystyle {\frac {f+c}{b}}={\frac {e}{d}}}$

${\displaystyle f={\frac {eb}{d}}-c}$

${\displaystyle fd+cd=eb}$

${\displaystyle fd+cd=({\frac {fb}{d}}-a)b}$

${\displaystyle fd+cd={\frac {fb^{2}}{d}}-ab}$

${\displaystyle fd+cd={\frac {fb^{2}-abd}{d}}}$

${\displaystyle fd^{2}+cd^{2}=fb^{2}-abd}$

${\displaystyle fd^{2}-fb^{2}=-(cd^{2}+abd)}$

${\displaystyle f(d^{2}-b^{2})=-d(cd+ab)}$

${\displaystyle f={\frac {-d(cd+ab)}{d^{2}-b^{2}}}}$

• Şimdi, üçgen formüllerinde yukarıda elde ettiğimiz ${\displaystyle e={\frac {dbc+ad^{2}}{b^{2}-d^{2}}}}$ ve ${\displaystyle f={\frac {cd^{2}+abd}{b^{2}-d^{2}}}}$ ifadelerini yerine koyarak devam edeceğiz.

${\displaystyle 2s={\frac {dbc+ad^{2}}{b^{2}-d^{2}}}+a+{\frac {cd^{2}+abd}{b^{2}-d^{2}}}+c+b}$

${\displaystyle s={\frac {dbc+ad^{2}}{b^{2}-d^{2}}}+a+{\frac {cd^{2}+abd}{b^{2}-d^{2}}}+c+b]}$

${\displaystyle s={\frac {1}{2}}[{\frac {dbc+ad^{2}+a(b^{2}-d^{2})+cd^{2}+abd+c(b^{2}-d^{2})+b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle s={\frac {1}{2}}[{\frac {dcb+ad^{2}+ab^{3}-ad^{2}+cd^{2}+abd+cb^{2}-cd^{2}+b^{3}-bd^{2}}{b^{2}-d^{2}}}]}$

${\displaystyle s={\frac {1}{2}}[{\frac {bd(c+a)+b^{2}(c+a)+b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle s={\frac {1}{2}}[{\frac {(bd+b^{2})(c+a)+b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle s={\frac {1}{2}}[{\frac {b(d+b)(c+a)}{(b+d)(b-d)}}+{\frac {b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle s={\frac {1}{2}}[{\frac {b(c+a)+b(b-d)}{b-d}}]}$

${\displaystyle s={\frac {b(c+a+b-d)}{2(b-d)}}}$

• Şimdi, ${\displaystyle (s-(e+a))}$'yı hesaplayalım.

${\displaystyle s-(e+a)={\frac {b(c+a+b-d)}{2(b-d)}}-{\frac {d(ad+cb)}{b^{2}-d^{2}}}-a}$

${\displaystyle =[{\frac {dcb+ad^{2}}{2(b^{2}-d^{2})}}+{\frac {a}{2}}+{\frac {cd^{2}+abd}{2(b^{2}-d^{2})}}+{\frac {c}{2}}+{\frac {b}{2}}]-[{\frac {dcb+ad^{2}}{b^{2}-d^{2}}}]-a}$

${\displaystyle ={\frac {dcb+ad^{2}}{2(b^{2}-d^{2})}}+{\frac {a}{2}}+{\frac {cd^{2}+abd}{2(b^{2}-d^{2})}}+{\frac {c}{2}}+{\frac {b}{2}}-{\frac {dcb+ad^{2}}{b^{2}-d^{2}}}-a}$

${\displaystyle =-{\frac {dcb+ad^{2}}{2(b^{2}-d^{2})}}-{\frac {a}{2}}+{\frac {cd^{2}+abd}{2(b^{2}-d^{2})}}+{\frac {c}{2}}+{\frac {b}{2}}}$

${\displaystyle =-{\frac {1}{2}}[{\frac {dcb+ad^{2}}{b^{2}-d^{2}}}+a-{\frac {(cd^{2}+abd)}{b^{2}-d^{2}}}-c-b]}$

${\displaystyle =-{\frac {1}{2}}[{\frac {dcb+ad^{2}+a(b^{2}-d^{2})-cd^{2}-abd-c(b^{2}-d^{2})-b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle =-{\frac {1}{2}}[{\frac {dcb+ab^{2}-abd-cd^{2}-b^{3}+bd^{2}}{b^{2}-d^{2}}}]}$

${\displaystyle =-{\frac {1}{2}}[{\frac {bd(c-a)-b^{2}(c-a)-b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle =-{\frac {1}{2}}[{\frac {(bd-b^{2})(c-a)}{b^{2}-d^{2}}}-{\frac {b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle =-{\frac {b(d-b)(c-a)}{2(b-d)(b+d)}}+{\frac {b}{2}}}$

${\displaystyle ={\frac {b(c-a)+b(b+d)}{2(b+d)}}}$

${\displaystyle ={\frac {b(c-a+b+d)}{2(b+d)}}}$

• Benzer şekilde, şimdi ${\displaystyle (s-(f+c))}$'yi a, b, c ve d cinsinden hesaplayalım.

${\displaystyle s-(f+c)={\frac {b(c+a+d-b)}{2(b-d)}}-{\frac {cd^{2}+abd}{b^{2}-d^{2}}}-c}$

${\displaystyle =[{\frac {dcb+ad^{2}}{2(b^{2}-d^{2})}}+{\frac {a}{2}}+{\frac {cd^{2}+abd}{2(b^{2}-d^{2})}}+{\frac {c}{2}}+{\frac {b}{2}}]-[{\frac {cd^{2}+abd}{b^{2}-d^{2}}}]-c}$

${\displaystyle ={\frac {dcb+ad^{2}}{2(b^{2}-d^{2})}}+{\frac {a}{2}}+{\frac {cd^{2}+abd}{2(b^{2}-d^{2})}}+{\frac {c}{2}}+{\frac {b}{2}}-{\frac {cd^{2}+abd}{b^{2}-d^{2}}}-c}$

${\displaystyle ={\frac {dcb+ad^{2}}{2(b^{2}-d^{2})}}+{\frac {a}{2}}-{\frac {cd^{2}+abd}{2(b^{2}-d^{2})}}-{\frac {c}{2}}+{\frac {b}{2}}}$

${\displaystyle =-{\frac {1}{2}}[{\frac {-dcb+ad^{2}}{b^{2}-d^{2}}}-a+{\frac {cd^{2}+abd}{b^{2}-d^{2}}}+c-b]}$

${\displaystyle =-{\frac {1}{2}}[{\frac {-dcb-ad^{2}-a(b^{2}-d^{2})+cd^{2}+abd+c(b^{2}-d^{2})-b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle =-{\frac {1}{2}}[{\frac {-dcb-ad^{2}-ab^{2}+ad^{2}+cd^{2}+abd+cb^{2}-cd^{2}-b^{3}+bd^{2}}{b^{2}-d^{2}}}]}$

${\displaystyle =-{\frac {1}{2}}[{\frac {-dcb-ab^{2}+abd+cb^{2}-b^{3}+bd^{2}}{b^{2}-d^{2}}}]}$

${\displaystyle =-{\frac {1}{2}}[{\frac {-bd(c-a)+b^{2}(c-a)-b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle =-{\frac {1}{2}}[{\frac {-(bd-b^{2})(c-a)}{b^{2}-d^{2}}}-{\frac {b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle ={\frac {-b(b-d)(c-a)}{2(b-d)(b+d)}}+{\frac {b}{2}}}$

${\displaystyle ={\frac {-b(c-a)+b(b+d)}{2(b+d)}}}$

${\displaystyle ={\frac {b(-c+a+b+d)}{2(b+d)}}}$

• Şimdi ${\displaystyle (s-b)}$'yi hesaplayalım.

${\displaystyle (s-b)={\frac {dcb+ad^{2}}{2(b^{2}-d^{2})}}+{\frac {a}{2}}+{\frac {cd^{2}+abd}{2(b^{2}-d^{2})}}+{\frac {c}{2}}+{\frac {b}{2}}-b}$

${\displaystyle ={\frac {dcb+ad^{2}}{2(b^{2}-d^{2})}}+{\frac {a}{2}}+{\frac {cd^{2}+abd}{2(b^{2}-d^{2})}}+{\frac {c}{2}}-{\frac {b}{2}}}$

${\displaystyle ={\frac {1}{2}}[{\frac {dcb+ad^{2}}{b^{2}-d^{2}}}+a+{\frac {cd^{2}+abd}{b^{2}-d^{2}}}+c-b]}$

${\displaystyle ={\frac {1}{2}}[{\frac {dcb+ad^{2}+a(b^{2}-d^{2})+cd^{2}+abd+c(b^{2}-d^{2})-b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle ={\frac {1}{2}}[{\frac {dcb+ad^{2}+ab^{2}-ad^{2}+cd^{2}+abd+cb^{2}-cd^{2}-b^{3}+bd^{2}}{b^{2}-d^{2}}}]}$

${\displaystyle ={\frac {1}{2}}[{\frac {bd(c+a)+b^{2}(c+a)-b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle ={\frac {1}{2}}[{\frac {b(b+d)(c+a)}{b^{2}-d^{2}}}-{\frac {b(b^{2}-d^{2})}{b^{2}-d^{2}}}]}$

${\displaystyle ={\frac {b(b+d)(c+a)}{2(b+d)(b-d)}}-{\frac {b}{2}}}$

${\displaystyle ={\frac {b(c+a)-b(b-d)}{2(b-d)}}}$

${\displaystyle ={\frac {b(c+a-b+d)}{2(b-d)}}}$

• Şimdi dörtgenin alanını a, b, c, d cinsinden hesaplamaya hazırız.

${\displaystyle A={\frac {b^{2}-d^{2}}{b^{2}}}{\sqrt {({\frac {b(c-a+b+d)}{2(b+d)}})({\frac {b(c+a-b+d)}{2(b-d)}})({\frac {b(-c+a+b+d)}{2(b+d)}})({\frac {b(c+a+b-d)}{2(b-d)}})}}}$

${\displaystyle A={\frac {b^{2}-d^{2}}{b^{2}}}{\sqrt {{\frac {b^{4}}{(b-d)^{2}(b+d)^{2}}}({\frac {-a+b+c+d}{2}})({\frac {a-b+c+d}{2}})({\frac {a+b-c+d}{2}})({\frac {a+b+c-d}{2}})}}}$

${\displaystyle A={\frac {b^{2}-d^{2}}{b^{2}}}.{\frac {b^{2}}{b^{2}-d^{2}}}{\sqrt {({\frac {-a+b+c+d}{2}})({\frac {a-b+c+d}{2}})({\frac {a+b-c+d}{2}})({\frac {a+b+c-d}{2}})}}}$

${\displaystyle A={\sqrt {({\frac {-a+b+c+d-a+a}{2}})({\frac {a-b+c+d-b+b}{2}})({\frac {a+b-c+d-c+c}{2}})({\frac {a+b+c-d-d+d}{2}})}}}$

${\displaystyle A={\sqrt {({\frac {a+b+c+d}{2}}-a)({\frac {a+b+c+d}{2}}-b)({\frac {a+b+c+d}{2}}-c)({\frac {a+b+c+d}{2}}-d)}}}$

Bu nedenle,

${\displaystyle A={\sqrt {(s-a)(s-b)(s-c)(s-d)}}}$

burada s, kirişler dörtgenin yarı çevresi yani

${\displaystyle s={\frac {a+b+c+d}{2}}}$'dir.

Kirişler dörtgeni olmayan dörtgenlere genişletme

Kirişler dörtgeni olmayan dörtgenler söz konusu olduğunda, Brahmagupta formülü, dörtgenin iki zıt açısının ölçüleri dikkate alınarak genişletilebilir:

${\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}\theta }}}$

burada θ herhangi iki zıt açının toplamının yarısıdır. (Hangi zıt açı çiftinin seçimi önemsizdir: diğer iki açı alınırsa, toplamlarının yarısı 180° − θ'dir. cos(180° − θ) = −cos θ olduğundan, cos²(180° − θ) = cos² θ ederiz. Bu daha genel formül Bretschneider formülü olarak bilinir.

Bir dörtgenin zıt açılarının toplamının 180°'ye eşit olması, kirişler dörtgeninin (ve nihayetinde çevre açıların) bir özelliğidir. Sonuç olarak, bir çevrel dörtgen durumunda, θ açısı 90°'dir, bu nedenle

${\displaystyle abcd\cos ^{2}\theta =abcd\cos ^{2}\left(90^{\circ }\right)=abcd\cdot 0=0,}$

olup Brahmagupta formülünün temel biçimini verir. İkinci denklemden, bir kirişler dörtgenin alanının, verilen kenar uzunluklarına sahip herhangi bir dörtgen için mümkün olan maksimum alan olduğu sonucu çıkar.

Coolidge tarafından kanıtlanan ilgili bir formül de genel bir dışbükey dörtgen alanını verir.[2]

${\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-\textstyle {1 \over 4}(ac+bd+pq)(ac+bd-pq)}}}$

burada p ve q, dörtgenin köşegenlerinin uzunluklarıdır. Batlamyus teoremine göre bir kirişler dörtgeninde pq = ac + bd 'dir ve Coolidge formülü, Brahmagupta formülüne indirgenir.

İlgili teoremler

• Bir üçgenin alanını hesaplamak için Heron formülü, d = 0 alınarak elde edilen özel durumdur.
• Brahmagupta formülünün genel ve genişletilmiş biçimi arasındaki ilişki, Kosinüs yasasının Pisagor teoremini nasıl genişlettiğine benzer.
• Maley ve diğerleri tarafından açıklandığı gibi, çemberler üzerindeki genel çokgenlerin alanı için giderek karmaşıklaşan kapalı biçimli formüller mevcuttur.[3]

Kaynakça

1. Hess, Albrecht, "A highway from Heron to Brahmagupta", Forum Geometricorum 12 (2012), 191–192.
2. J. L. Coolidge, "A Historically Interesting Formula for the Area of a Quadrilateral", American Mathematical Monthly, 46 (1939) ss. 345-347.
3. Maley (2005). "On the areas of cyclic and semicyclic polygons". Advances in Applied Mathematics. 34 (4): 669-689. doi:10.1016/j.aam.2004.09.008.

Dış bağlantılar

• Brahmagupta's formula at ProofWiki
• Eric W. Weisstein, Brahmagupta's Formula (MathWorld)

Bu makale, Creative Commons Attribution/Share-Alike Lisansı altında lisanslanan PlanetMath üzerinde Brahmagupta formülünün kanıtından materyal içermektedir.