Geometrik ortalama teoremi

Dik üçgen yükseklik teoremi veya geometrik ortalama teoremi, bir dik üçgendeki hipotenüs üzerindeki yükseklik uzunluğu ile hipotenüs üzerinde oluşturduğu iki doğru parçası arasındaki ilişkiyi tanımlayan temel geometrinin bir sonucudur. İki doğru parçasının geometrik ortalamasının yüksekliğe eşit olduğunu belirtir.

gri karenin alanı = gri dikdörtgenin alanı:
${\displaystyle h^{2}=pq\Leftrightarrow h={\sqrt {pq}}}$

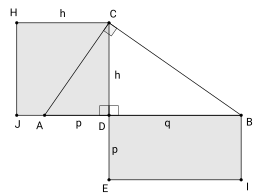
Teorem ve uygulamaları

${\displaystyle q}$'nun değerini 1 alarak ${\displaystyle {\sqrt {p}}}$'nin inşa edilmesi

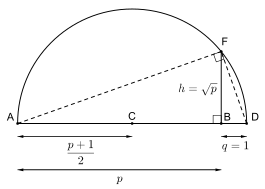
Eğer ${\displaystyle h}$, dik üçgende yüksekliği ve ${\displaystyle p}$ ile ${\displaystyle q}$ hipotenüs üzerindeki parçaları gösteriyorsa, teorem şu şekilde ifade edilebilir:[1]

${\displaystyle h={\sqrt {pq}}}$

veya alan cinsinden ifade edilirse:

${\displaystyle h^{2}=pq.}$

AO-GO eşitsizliği

Sonraki versiyon, bir dikdörtgeni cetvel ve pergel ile kare yapmak için, yani belirli bir dikdörtgene eşit alanlı bir kare oluşturmak için bir yöntem sağlar. Kenarları ${\displaystyle p}$ ve ${\displaystyle q}$ olan böyle bir dikdörtgenin, sol üst köşesini ${\displaystyle D}$ ile gösterelim. Şimdi ${\displaystyle q}$ parçasını soluna ${\displaystyle p}$ kadar uzatalım (${\displaystyle D}$'de ortalanmış ${\displaystyle AE}$ yayını kullanarak) ve çapı yeni parça ${\displaystyle p+q}$ ve uç noktaları ${\displaystyle A}$ ile ${\displaystyle B}$ olan bir yarım çember çizelim. Sonra ${\displaystyle D}$'deki çapa, ${\displaystyle C}$'deki yarım çemberi kesen dik bir doğru çizelim. Thales teoremine göre ${\displaystyle C}$ ve çap, ${\displaystyle DC}$ doğru parçasının yükseklik olduğu bir dik üçgen oluşturur, dolayısıyla ${\displaystyle DC}$ dikdörtgenin alanına eşit alanlı olan bir karenin kenarıdır. Yöntem ayrıca kare köklerin oluşturulmasına da izin verir (İnşa edilebilir sayıya bakın), çünkü 1 genişliğinde bir dikdörtgenden başlayarak inşa edilen karenin, dikdörtgenin diğer kenar uzunluğunun kareköküne eşit bir kenar uzunluğu olacaktır.[1]

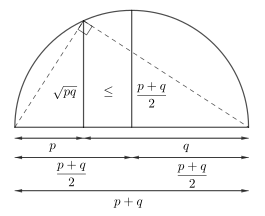
Teorem, iki sayı durumunda AO-GO eşitsizliğinin geometrik bir kanıtını sağlamak için kullanılabilir. ${\displaystyle p}$ ve ${\displaystyle q}$ sayıları için ${\displaystyle p+q}$ çapında yarım çember oluşturulur. Şimdi yükseklik, iki sayının geometrik ortalamasını ve yarıçapı aritmetik ortalamasını temsil eder. Yükseklik her zaman yarıçapa eşit veya daha küçük olduğu için bu eşitsizliği ortaya çıkarır.[2]

Kiriş teoreminin özel bir durumu olarak geometrik ortalama teoremi:
${\displaystyle |CD||DE|=|AD||DB|\Leftrightarrow h^{2}=pq}$

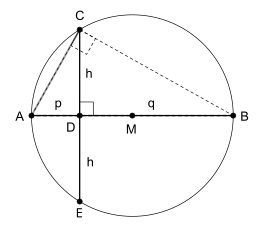
Geometrik ortalama teoremi, Thales teoreminin tersi, dik üçgenin hipotenüsünün çevrel çemberinin çapı olmasını sağladığından, ayrıca bir çember için kesişen kirişler teoreminin özel bir durumu olarak düşünülebilir.[1]

İfadenin tersi de doğrudur. Yüksekliğin, kendisi tarafından oluşturulan iki doğru parçasının geometrik ortalamasına eşit olduğu herhangi bir üçgen, bir dik üçgendir.

Tarihçe

Teorem genellikle, onu Elemanlar VI. kitabında 8. önermenin doğal sonucu olarak ifade eden Öklid'e (y. MÖ 360-280) atfedilir. II. Kitabın 14. önermesinde, Öklid bir dikdörtgenin karesini almak için burada verilen yönteme esasen uyan bir yöntem verir. Bununla birlikte, Öklid, geometrik ortalama teoremine dayanmak yerine, yapının doğruluğu için biraz daha karmaşık bir kanıt sağlar.[1][3]

İspat

Benzerliğe dayanarak

${\displaystyle \triangle ABC\sim \triangle ADC\sim \triangle DBC}$

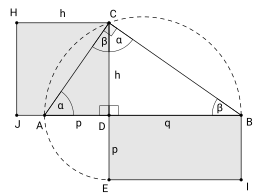
Teoremin kanıtı :

${\displaystyle \triangle ADC}$ ve ${\displaystyle \triangle BCD}$ üçgenleri benzerdir, çünkü:

• ${\displaystyle \triangle ABC{\text{ ve }}\triangle ACD}$ üçgenlerini düşünün, burada ${\displaystyle \angle ACB=\angle ADC=90^{\circ }}$ ve ${\displaystyle \angle BAC=\angle CAD}$'dir, bu nedenle AA postülatına göre ${\displaystyle \triangle ABC\sim \triangle ACD}$'dir.
• Ayrıca, ${\displaystyle \triangle ABC{\text{ ve }}\triangle BCD}$ üçgenleri düşünün, burada ${\displaystyle \angle ACB=\angle BDC=90^{\circ }}$ ve ${\displaystyle \angle ABC=\angle CBD}$'dir, bu nedenle AA postülatına göre ${\displaystyle \triangle ABC\sim \triangle BCD}$'dir.

Bu nedenle, her iki üçgen ${\displaystyle \triangle ACD}$ ve ${\displaystyle \triangle BCD}$, ${\displaystyle \triangle ABC}$ üçgenine ve kendilerine benzerdir, yani ${\displaystyle \triangle ACD\sim \triangle ABC\sim \triangle BCD}$'dir.

Benzerlik nedeniyle aşağıdaki eşitlik oranlarını elde ederiz ve cebirsel yeniden düzenlenmesi bize teoremi verir:[1]

${\displaystyle {\frac {h}{p}}={\frac {q}{h}}\,\Leftrightarrow \,\ h^{2}=pq\,\Leftrightarrow \,\ h={\sqrt {pq}}\qquad (h,\ p,\ q\ >0)}$

Tersinin kanıtı:

Tersi için ${\displaystyle h^{2}=pq}$ eşitliğini sağlanan bir ${\displaystyle \triangle ABC}$ üçgenimiz vardır ve ${\displaystyle C}$'deki açının dik açı olduğunun gösterilmesi gerekir. Şimdi ${\displaystyle h^{2}=pq}$ yüzünden ayrıca ${\displaystyle {\tfrac {h}{p}}={\tfrac {q}{h}}}$ ifadesine sahibiz. ${\displaystyle \angle ADC=\angle CDB}$ eşitliği ile birlikte üçgenler ${\displaystyle \triangle ADC}$ ve ${\displaystyle \triangle BDC}$ eşit büyüklükte bir açıya ve aynı orana sahip karşılıklı kenar çiftlerine sahiptir. Bu, üçgenlerin benzer olduğu anlamına gelir ve sonuç aşağıdaki şekilde ifade edilebilir:

${\displaystyle \angle ACB=\angle ACD+\angle DCB=\angle ACD+(90^{\circ }-\angle DBC)=\angle ACD+(90^{\circ }-\angle ACD)=90^{\circ }}$

Pisagor teoremine dayanarak

Pisagor teoremi ile kanıt

Geometrik ortalama teoreminin kurgusunda, Pisagor teoreminin uygulanabileceği üç dik üçgen ${\displaystyle \triangle ABC}$, ${\displaystyle \triangle ADC}$ ve ${\displaystyle \triangle DBC}$ vardır:

${\displaystyle h^{2}=a^{2}-q^{2}}$,

${\displaystyle h^{2}=b^{2}-p^{2}}$ ve

${\displaystyle c^{2}=a^{2}+b^{2}}$

İlk 2 iki denklemi taraf tarafa toplamak ve ardından üçüncüyü kullanmak aşağıdaki ifadenin elde edilmesini sağlar:

${\displaystyle 2h^{2}=a^{2}+b^{2}-p^{2}-q^{2}=c^{2}-p^{2}-q^{2}=(p+q)^{2}-p^{2}-q^{2}=2pq}$.

İkiye bölerek sadeleştirme, sonunda geometrik ortalama teoreminin formülünü verir.[4]

Parçalarına ayırma ve yeniden düzenlemeye dayanarak

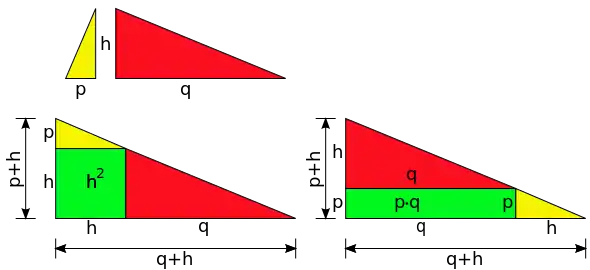
Dik üçgeni ${\displaystyle h}$ yüksekliği boyunca parçalarına ayırmak, iki farklı şekilde artırılabilen ve ${\displaystyle p+h}$ ve ${\displaystyle q+h}$ uzunluklarına sahip dikey kenarları olan daha büyük bir dik üçgen olarak düzenlenebilen iki benzer üçgen verir. Bu tür bir düzenleme, bu tamamlamak için ${\displaystyle h^{2}}$ alanına sahip bir kare alan ve ${\displaystyle pq}$ alanına sahip diğer bir dikdörtgen gerektirir. Her iki düzenleme de aynı üçgeni verdiğinden, kare ve dikdörtgenin alanları aynı olmalıdır.

Kesme haritalamaya dayanarak

Yüksekliğin karesi, ${\displaystyle p}$ ve ${\displaystyle q}$ kenarları ile eşit alanlı bir dikdörtgene, üç kesme haritalama yardımıyla dönüştürülebilir (kesme haritalama alanı korur):

Ön görüntü olarak orijinal kareden başlayarak ilişkili sabit çizgileriyle (noktalı) kesme haritalamaları, her paralelkenar, solundaki şeklin kesme haritalamasının görüntüsünü gösterir.

Kaynakça

1. Hartmut Wellstein, Peter Kirsche: Elementargeometrie. Springer, 2009, 9783834808561, pp. 76-77 (German, Google Kitaplar'da online copy)
2. Claudi Alsina, Roger B. Nelsen: Icons of Mathematics: An Exploration of Twenty Key Images. MAA 2011, 9780883853528, pp. 31–32 (Google Kitaplar'da online copy)
3. Öklid: Elemanlar, book II – prop. 14, book VI – prop. 8, (online copy)
4. Ilka Agricola, Thomas Friedrich: Elementary Geometry. AMS 2008, 9780821843475, p. 25 (Google Kitaplar'da online copy, s. 25,)

Dış bağlantılar

• Cut-the-knot.org'da Geometrik Ortalama