Kesişen kirişler teoremi

Kesişen kirişler teoremi veya sadece kiriş teoremi, bir çember içinde kesişen iki kiriş tarafından oluşturulan dört doğru parçasının ilişkisini tanımlayan temel geometrideki bir ifadedir. Her bir kirişteki doğru parçalarının uzunluklarının çarpımlarının eşit olduğunu belirtir. Öklid'in Unsurlarının 3. kitabının 35. önermesidir.

${\displaystyle |AS|\cdot |SC|=|BS|\cdot |SD|}$

${\displaystyle {\begin{aligned}&|AS|\cdot |SC|=|BS|\cdot |SD|\\=&(r+d)\cdot (r-d)=r^{2}-d^{2}\end{aligned}}}$

${\displaystyle \triangle ASD\sim \triangle BSC}$

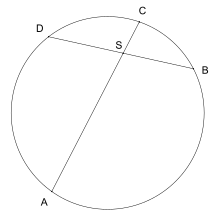
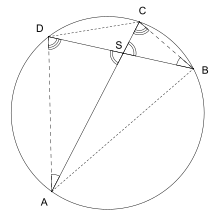
Açıklama

Daha net olarak, bir ${\displaystyle S}$ noktasında kesişen iki kiriş ${\displaystyle AC}$ ve ${\displaystyle BD}$ için aşağıdaki denklem geçerlidir:

${\displaystyle |AS|\cdot |SC|=|BS|\cdot |SD|}$

Bunun tersi de doğrudur, yani ${\displaystyle S}$'de kesişen iki doğru parçası ${\displaystyle AC}$ ve ${\displaystyle BD}$ için yukarıdaki denklem doğruysa, bu durumda dört uç nokta ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ ve ${\displaystyle D}$ ortak bir çember üzerinde yer alır. Ya da başka bir deyişle, ${\displaystyle ABCD}$ dörtgeninin köşegenleri ${\displaystyle S}$'de kesişir ve yukarıdaki denklemi sağlanırsa bu bir kirişler dörtgenidir.

Kiriş teoremindeki iki çarpımın değeri sadece kesişme noktası ${\displaystyle S}$'nin çember merkezinden uzaklığına bağlıdır ve ${\displaystyle S}$'nin kuvvetinin mutlak değeri olarak adlandırılır, daha net olarak aşağıdaki şekilde ifade edilebilir:

${\displaystyle |AS|\cdot |SC|=|BS|\cdot |SD|=r^{2}-d^{2}}$

burada ${\displaystyle r}$, çemberin yarıçapı ve ${\displaystyle d}$, çemberin merkezi ile kesişme noktası ${\displaystyle S}$ arasındaki mesafedir. Bu özellik, doğrudan kiriş teoremini ${\displaystyle S}$ ve çemberin merkezi ${\displaystyle M}$'den geçen üçüncü bir kirişe uygulamaktan kaynaklanır (çizime bakın).

Teorem, benzer üçgenler kullanılarak (çevre açı teoremi aracılığıyla) kanıtlanabilir. ${\displaystyle \triangle ASD}$ ve ${\displaystyle \triangle BSC}$ üçgenlerinin açılarını düşünün:

${\displaystyle {\begin{aligned}\angle ADS&=\angle BCS\,\ ({\text{AB yayını gören çevre açılar}})\\\angle DAS&=\angle CBS\,\ ({\text{CD yayını gören çevre açılar}})\\\angle ASD&=\angle BSC\,\ ({\text{zıt açılar}})\end{aligned}}}$

Bu, ${\displaystyle \triangle ASD}$ ve ${\displaystyle \triangle BSC}$ üçgenlerinin benzer olduğu ve dolayısıyla,

${\displaystyle {\frac {AS}{SD}}={\frac {BS}{SC}}\Leftrightarrow |AS|\cdot |SC|=|BS|\cdot |SD|}$

Teğet-kesen teoremi ve kesişen sekantlar teoreminin yanında, kesişen kiriş teoremi, iki kesişen doğru ve bir çember hakkında daha genel bir teoremin üç temel durumundan birini temsil eder - noktanın kuvveti teoremini.

Kaynakça

• Glaister, Paul (Ocak 2007), "Intersecting Chords Theorem: 30 Years on", Mathematics in School, 36 (1), s. 22
• Shawyer, Bruce (2010), "Explorations in Geometry", World scientific, s. 14, ISBN 9789813100947
• Schupp, Hans (1977), Elementargeometrie (Almanca), Schöningh, Paderborn, s. 149, ISBN 3-506-99189-2
• Schülerduden - Mathematik I (Almanca) (8. bas.), Mannheim: Bibliographisches Institut & F.A. Brockhaus, 2008, ss. 415-417, ISBN 978-3-411-04208-1

Dış bağlantılar

• Intersecting Chords Theorem @ cut-the-knot.org
• Intersecting Chords Theorem @ proofwiki.org
• Eric W. Weisstein, Chord (MathWorld)
• Geogebra'da iki etkileşimli animasyon: "Intersecting chord theorem" ve "Intersecting Chords Theorem"