Gibbs fenomeni

Matematikte, Henry Wilbraham (1848) tarafından keşfedilen Gibbs fenomeni, Henry Wilbraham (1848)[1] ve J. Willard Gibbs (1899) tarafından yeniden keşfedilen, J. Willard Gibbs (1899),[2] bir parça parça Fourier serileri sürekli türevlenebilir periyodik fonksiyonun davranışı burada tuhaf şekilde olduğu için sıçramalı süreksizliktir: Fourier serilerinin n 'inci kısmi toplam fonksiyonunun kendisinin yukarıda kısmi toplamının maksimum artış olabilir, sıçramaya yakın büyük salınımlar vardır. Aşım frekansı arttıkça ölüp, ama sonlu bir sınırı yaklaşımlar değildir. [3]

Bu işaret işleme içinde zil sesi garipliği birinci durumdur.

Fenomenin resmi bir matematiksel açıklaması

Diyelimki ${\displaystyle f:{\mathbb {R} }\to {\mathbb {R} }}$ bir parça parça sürekli türevlenebilir fonksiyonu olsun ${\displaystyle L>0}$ bazı periyodu ile periyodiktir.${\displaystyle x_{0}}$ bazı noktalarında varsayalımki, ${\displaystyle f}$ ${\displaystyle a}$ bir sıfır olmayan boşluk ile farklı ${\displaystyle f}$fonksiyonunun sol limiti ${\displaystyle f(x_{0}^{-})}$ ve sağ limit ${\displaystyle f(x_{0}^{+})}$:

${\displaystyle f(x_{0}^{+})-f(x_{0}^{-})=a\neq 0.}$

her N ≥ 1 pozitif tam sayı için, diyelimki S_N f Ninci kısmi Fourier serisi

${\displaystyle S_{N}f(x):=\sum _{-N\leq n\leq N}{\hat {f}}(n)e^{\frac {2i\pi nx}{L}}={\frac {1}{2}}a_{0}+\sum _{n=1}^{N}\left(a_{n}\cos \left({\frac {2\pi nx}{L}}\right)+b_{n}\sin \left({\frac {2\pi nx}{L}}\right)\right),}$

olsun burada the Fourier katsayıları ${\displaystyle {\hat {f}}(n),a_{n},b_{n}}$ genellikle şu formülle verilir

${\displaystyle {\hat {f}}(n):={\frac {1}{L}}\int _{0}^{L}f(x)e^{-2i\pi nx/L}\,dx}$

${\displaystyle a_{n}:={\frac {2}{L}}\int _{0}^{L}f(x)\cos \left({\frac {2\pi nx}{L}}\right)\,dx}$

${\displaystyle b_{n}:={\frac {2}{L}}\int _{0}^{L}f(x)\sin \left({\frac {2\pi nx}{L}}\right)\,dx.}$

o zaman

${\displaystyle \lim _{N\to \infty }S_{N}f\left(x_{0}+{\frac {L}{2N}}\right)=f(x_{0}^{+})+a\cdot (0.089490\dots )}$

ve

${\displaystyle \lim _{N\to \infty }S_{N}f\left(x_{0}-{\frac {L}{2N}}\right)=f(x_{0}^{-})-a\cdot (0.089490\dots )}$

ama

${\displaystyle \lim _{N\to \infty }S_{N}f(x_{0})={\frac {f(x_{0}^{-})+f(x_{0}^{+})}{2}}.}$

Daha genel, eğer ${\displaystyle x_{N}}$ ${\displaystyle N\to \infty }$ olarak ${\displaystyle x_{0}}$ a yakınsaklığı bu gerçek sayıların herhangi dizisidir, ve eğer boşluk a pozitif ise

${\displaystyle \limsup _{N\to \infty }S_{N}f(x_{N})\leq f(x_{0}^{+})+a\cdot (0.089490\dots )}$

ve

${\displaystyle \liminf _{N\to \infty }S_{N}f(x_{N})\geq f(x_{0}^{-})-a\cdot (0.089490\dots ).}$

Eğer boşluk a yerine is negatif, bir üst limit ile alt limit kavşaklarına, ve ayrıca yukarıdaki iki eşitsizlik içinde kavşak ≤ ve ≥ işaretlerine gerek vardır.

Kare dalga örnekleri

Harmonikleri giderek artan sayıda bir kare dalganın katkı sentezi Animasyon. Harmoniklerin sayısı büyükse özellikle Gibbs fenomeni görülebilir.

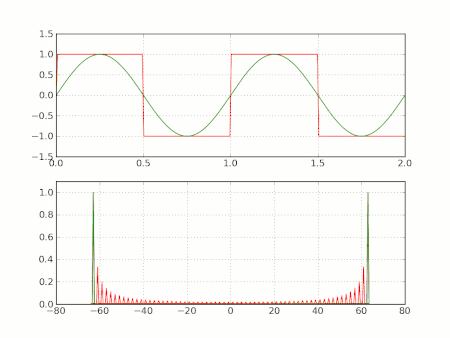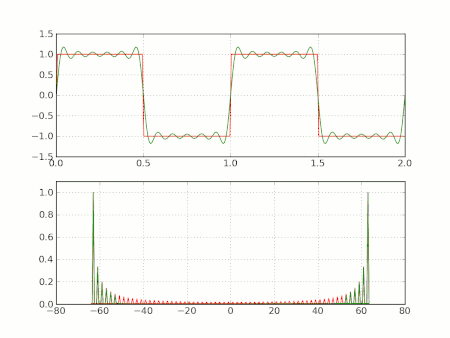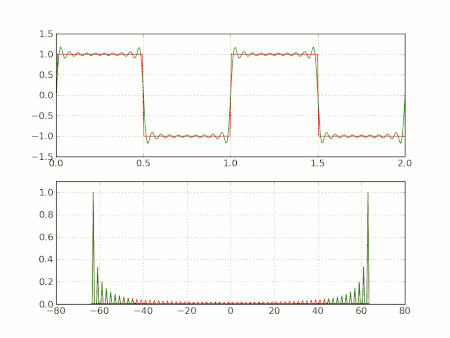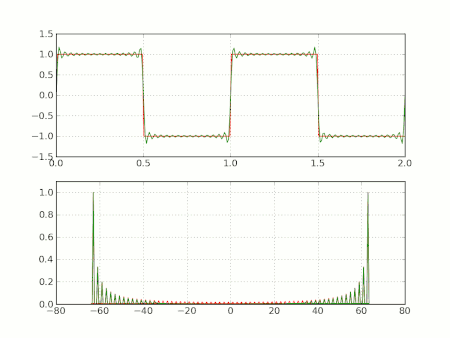
Şimdi daha önce açıklanan kare dalga durumunda yukarıdaki Gibbs fenomeni açıklanmaktadır. L periyodu durumu içinde is ${\displaystyle 2\pi }$,${\displaystyle x_{0}}$ süreksizliği sıfırdadır, ve sıçrama a ${\displaystyle \pi /2}$ ya eşittir. Basitlik için bize sadece N durumu ile ilgilenirsek bu çifttir (the case of odd Ntek'in durum çok benzerdir). Ve

${\displaystyle S_{N}f(x)=\sin(x)+{\frac {1}{3}}\sin(3x)+\cdots +{\frac {1}{N-1}}\sin((N-1)x).}$

ele ederiz ${\displaystyle x=0}$ yerine koyma ile,

${\displaystyle S_{N}f(0)=0={\frac {-{\frac {\pi }{4}}+{\frac {\pi }{4}}}{2}}={\frac {f(0^{-})+f(0^{+})}{2}}}$

elde ederiz Yukarıda belirtildiği gibi. sonuç olarak,

${\displaystyle S_{N}f\left({\frac {2\pi }{2N}}\right)=\sin \left({\frac {\pi }{N}}\right)+{\frac {1}{3}}\sin \left({\frac {3\pi }{N}}\right)+\cdots +{\frac {1}{N-1}}\sin \left({\frac {(N-1)\pi }{N}}\right).}$

elde ederiz Eğer normalize sinc fonksiyonu tanıtılırsa, ${\displaystyle \operatorname {sinc} (x)\,}$,biz bunu yeniden yazabiliriz

${\displaystyle S_{N}f\left({\frac {2\pi }{2N}}\right)={\frac {\pi }{2}}\left[{\frac {2}{N}}\operatorname {sinc} \left({\frac {1}{N}}\right)+{\frac {2}{N}}\operatorname {sinc} \left({\frac {3}{N}}\right)+\cdots +{\frac {2}{N}}\operatorname {sinc} \left({\frac {(N-1)}{N}}\right)\right].}$

olarak yeniden yazabiliriz Ama kare braketlerin içinde bağıntılar ${\displaystyle \int _{0}^{1}\operatorname {sinc} (x)\ dx}$ integraline yaklaşık bir sayısal integrasyondur(daha doğrusu, bu bir orta nokta kuralı aralıklı yaklaşım ${\displaystyle 2/N}$). sinc fonksiyonu sürekli olduğundan, bu yaklaşım fiili integraline yakınsamaktadır as ${\displaystyle N\to \infty }$. Böylece

${\displaystyle {\begin{aligned}\lim _{N\to \infty }S_{N}f\left({\frac {2\pi }{2N}}\right)&={\frac {\pi }{2}}\int _{0}^{1}\operatorname {sinc} (x)\,dx\\[8pt]&={\frac {1}{2}}\int _{x=0}^{1}{\frac {\sin(\pi x)}{\pi x}}\,d(\pi x)\\[8pt]&={\frac {1}{2}}\int _{0}^{\pi }{\frac {\sin(t)}{t}}\ dt\quad =\quad {\frac {\pi }{4}}+{\frac {\pi }{2}}\cdot (0.089490\dots ),\end{aligned}}}$

elde ederiz bu önceki bölümde iddia buydu. Benzer bir hesaplama gösterileri

${\displaystyle \lim _{N\to \infty }S_{N}f\left(-{\frac {2\pi }{2N}}\right)=-{\frac {\pi }{2}}\int _{0}^{1}\operatorname {sinc} (x)\ dx=-{\frac {\pi }{4}}-{\frac {\pi }{2}}\cdot (0.089490\dots ).}$

Sonuçları

Aşım ve doyumsuzluk tan gelen salınım, ve zil artefaktlar yani kırpma artefaktlar neden olduğu için sinyal işlemede, Gibbs fenomeni istenmez. Alçak geçiren filtre olması durumunda, bu farklı bir düşük-geçiş filtresi ile azaltılabilir veya ortadan kaldırılabilir.

MRI 'de, belirgin bir fenomen Gibbs sinyal yoğunluğu farklı bitişik bölgelerin varlığı kirliliklere neden olur. Bu en sık Gibbs fenomen syringomyeli görünümünü simüle spinal MR'da, karşılaşılır.

Ayrıca bakınız

• Pinsky fenomeni
• polinom yaklaşıklığı için Runge's fenomeni ile karşılaştırma
• Sigma yaklaşıklığı
• Sine integral

Notlar

1. Hewitt, Edwin; Hewitt, Robert E. (1979). "The Gibbs-Wilbraham phenomenon: An episode in fourier analysis". Archive for History of Exact Sciences. 21 (2). ss. 129-160. doi:10.1007/BF00330404. Erişim tarihi: 16 Eylül 2011. Available on-line at: National Chiao Tung University: Open Course Ware: Hewitt & Hewitt, 1979.
2. Andrew Dimarogonas. Vibration for engineers. ISBN 0-13-462938-8.
3. H. S. Carslaw (1930). Introduction to the theory of Fourier's series and integrals. Third Edition. New York: Dover Publications Inc. Chapter IX. 23 Temmuz 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 12 Temmuz 2014.

Kaynakça

• Gibbs, J. Willard (1898), "Fourier's Series", Nature, 59 (1522), s. 200, doi:10.1038/059200b0, ISSN 0028-0836
• Gibbs, J. Willard (1899), "Fourier's Series", Nature, 59 (1539), s. 606, doi:10.1038/059606a0, ISSN 0028-0836
• Michelson, A. A.; Stratton, S. W. (1898), "A new harmonic analyser", Philosophical Magazine, 5 (45), ss. 85-91
• Antoni Zygmund, Trigonometrical series, Dover publications, 1955.
• Wilbraham, Henry (1848), "On a certain periodic function", The Cambridge and Dublin Mathematical Journal, cilt 3, ss. 198-201, 17 Temmuz 2014 tarihinde kaynağından arşivlendi, erişim tarihi: 12 Temmuz 2014
• Paul J. Nahin, Dr. Euler's Fabulous Formula, Princeton University Press, 2006. Ch. 4, Sect. 4.

Dış bağlantılar

• Hazewinkel, Michiel, (Ed.) (2001), "Gibbs phenomenon", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
• Weisstein, Eric W., "Gibbs Phenomenon14 Temmuz 2014 tarihinde Wayback Machine sitesinde arşivlendi.". From MathWorld—A Wolfram Web Resource.
• Prandoni, Paolo, "Gibbs Phenomenon".
• Radaelli-Sanchez, Ricardo, and Richard Baraniuk, "Gibbs Phenomenon". The Connexions Project. (Creative Commons Attribution License)
• Horatio S Carslaw : Introduction to the theory of Fourier's series and integrals.pdf (introductiontot00unkngoog.pdf ) at archive.org