Nükleer bağlanma enerjisi

Nükleer bağlanma enerjisi, atomun çekirdeğini bileşenlerine ayırmak için gereken enerjidir. Bu bileşenler nötron, proton ve nükleondur. Bağ enerjisi genelde pozitif işaretlidir çünkü çoğu çekirdek parçalara ayrılmak için net bir enerjiye ihtiyacı vardır. Bu yüzden, genelde bir atomun çekirdeğinin kütlesi ayrı ayrı ölçüldüğünde daha azdır. Bu fark nükleer bağlanma enerjisidir ki bu enerji birbirini tutan bileşenlerin uyguladığı kuvvet tarafından sağlanır. Çekirdeği bileşenlerine ayırırken, kütlenin bir kısmı büyük bir enerjiye dönüştürülür (Einstein'ın denklemine göre E=mc²) bu yüzden biz kısım kütle eksilir, eksik kütlede bir fark yaratır çekirdekte. Bu eksik kütle kütle eksiği diye bilinir ve çekirdek oluşurken çıkan enerjiye takabül eder.

Bağlanma enerjisi terimi birden fazla nükleonla oluşan çekirdek bileşenlerine arılıkkenki enerji dengesine denk gelir ve bu durumda bağ enerjisi bileşenler için daha büyük olacaktır. Eğer yeni bir bağ enerjisi varsa hafif çekirdek füzyondanken veya ağır fizyondayken bir enerji kaybı gerçekleşecektir. Bu enerji, nükleer enerji, nükleer silah ve elektrik üretmek için kullanılabilir. Büyük çekirdek fizyona girerse, çıkan enerji fotonlar (gamma ışınları) ve çıkan diğer parçacıkların kinetik enerjisi olarak çıkar.

Nükleer bağ enerjisi ve kuvvetler ağır elementlerin milyon kat daha büyüktür. 

Kütle farkı, çekirdeğin bağ enerjisini oluşturur ve çekirdeğin parçalarının ayrı ölçülmüş hali ile birleşmiş haldeki halinin farkıdır. nükleer bağ enerjisini ölçmek 3 adımdan oluşan adımlarla mümkündür, burada kütle farkının oluşmasını kaybolan enerjiden çekerek bulunur.[1]

Giriş

Ortak izotopların nükleon başına bağlanma enerjisi.

Nükleer enerji, nükleer fiziğin birkaç temel presibine dayanır.

Nükleer enerji

Nükleer enerji emilimi veya salınımı nükleer reaksyon sırasında gerçekleşir veya radyoaktif çürümede; enerji alanlar endotermik salanlar ise egzotermik olarak adlandırılır. Enerji tüketimi veya salınımının nedeni giren ve çıkan ürünlerin arasındaki nükleer enerji bağının farkıdır.[2]

En iyi bilinen egzotermik nükleer tepkimeler fizyon ve füzyondur. Nükleer enerji atomik fizyon tarafından serbest bırakılabilir, tabii ki ağır bir çekirden örneğin uranyum parçalara ayrıldığında. Buradan çıkan enerji dünyanın dört bir yanında elektrik üretimi için kullanılmaktadır. Enerji aynı zamanda nükleer füzyonda da serbest bırakılır, burada işlev de tam terse doğru yani hafif elementten ağır element yaratma olayıdır örneğin hidrojeni helyuma çevirmik. Güneş ve diğer yıldızlar çekirdeğinde nükleer füzyon yaşarlar ve bu daha sonra da yüzeyden radyasyon olarak bırakılır. Bütün egzotermik tepkimelerde, çekirdeğin kütlesi enerjiye çevrilmelidir, ısı olarak salınım.

Bir değer bulabilmek için kaybolan veya gelen enerjiye, bileşenlerin nükleer enerji bağlar bilinmelidir.

Nükleer kuvvet

Elektronlar ve çekirdek elektrostatik kuvvet ile bir arada tutulur. Ek olarak, elektronlar bazen atomlar arasında paylaşılırlar veya transfer edilir,ve bu bağ kimyasal bağ olarak adlandırılır, ve kimyasal oluşumlar için sorumludur.[3]

Elektrostatik kuvvet çekirdeği bir arada tutmaz ,çünkü protonlar aynı yüke sahiptirler ve birbirini iterler. Sonuç olarak ayrı yönlere iterler birbiriniBuradan anlaşılacağı gibi çekirdeği bir arada tutmak için electrostatik burada işe yaramayacaktır.[3]

Bu yüzden yeni bir kuvvet, nükleer kuvvet, buarada işe girer ve çekirdeği bir arada tutar.. Bu çok güçlü bir etkileşimdir ve quarkları da bir arada tutar.

Nükleer kuvvet yakın mesafelerde çok büyük fakat uzak mesafelerde çok küçük olmalıdı, diğer türlü çekirdeği tutmak mümkün olamaz. Analoji yapmak istersen iki tane mıknatısı örnek olarak verebiliriz: mıknatıslar bir aradayken koparmak çok zordur fakat uzaktayken ihmal edilebilir durumdadırlar,.[3]

Kütleçekimi ve elektrostatik kuvvetlerin aksine nükleer kuvvet çok kısa mesafelerde geçerlidir.Büyük mesafelerde, elektrostatik kuvvet yönetir durumu. Bu sebepten dolayı, Bir balonun içindeki hidrojenin füzyona girmesi beklenemez çünkü elektrostatik kuvvet çok büyük ve çekirdeklerin bir araya gelmesi için yüksek bir enerji gereklidir. Ve bu koşullar ancak çok yüksek basınç ve sıcaklıklarda yaşanabilir, ki bir yıldız tam da adrestir ve yıldızı yıldız yapan da hidrojen füzyon yapmasıdır.

Çekirdek fiziği

Bir atomun çekirdeği birçok farklı şekilde bulunur. Hidrojende sadece proton bulunur, fakat deteryum ya bir proton bir nötron bulunur; helyumda iki proton iki nötron, ve karbonda, nitrojen ve oksijende - altı, yedi ve sekiz her birinden birer tane olmak şartıyla bulunur. rBir helyumun ağırlığı aslında parçacıklarını ayrı ayrı ölçülmüş halinden hada azdır. Aynı olay karbon nitrojen ve oksijen için de yaşanır Örneğin karbonun çekirdeği üç tane helyumdan daha hafiftir, ve bu sayı karbonun nükleuslarıyla aynıdır. Bu olay kütle eksiğidir.

Kütle eksiği

Kütle eksiği Albert Einstein formülü E = m c² ile açıklanabilir.Bu formülle, enerji eklersek kütle elde ederiz tam tersi yani kütle çıkarsa enerji kaybı olur sonucu çıkarılıbilir.

Eğer bu parçacıkların kombiasyonları fazladan eneji içerirse—örneğin, patlayıtı bir kutunun bir molekülünde—fazladan bir enerji ortaya çıkar, sonuçlarla kıyaslanınca tabi. (Tartma işlemi her şey soğuduktan sonra yapılmalıdır, fakat,fazla kütlenin oradan çıkması gerekiği gibi , ısı görülebilir) . Diğer bir bakış açısından bakmak gerekirse, eğer biz çekirdeği bileşenlerine ayırmak için enerji enjekte etmemiz gerekiyorsa, bileşenler ayrıldıktan öncekinden daha hafiftir. Sonraki durumda, enerji potansiyel enerji olarak tutulur, bu da kütlenin arttığını gösterir. Bu enerjinin kütle ile olan ilişkisinin en güzel örneklerinden biri, çünkü enerji ve kütle birbirine bağlıdırlar.

Gelecek senaryoda helyumun çekirdeği konu olacak: bileşenlerine ayırmak için belli bir enerji verilmelidir. Başka bir şekilde, Eğer olay diğer yönde hal alırsa, yani hidrojen atomları helyum oluştursalar, o zaman enerji salınır.Enerji basitçe bu formülden hesaplanır E = Δm c² her nükleüs için,burada Δm kütle eksiğini ifade eder

Oksijenden daha ağır elementler için, salınabilen enerji gittikçe azalır demire doğru gittikçe. Demirden daha ağır elementler için ise, enerji salınır bu sefer bölünerek. Bu da uranyumdan nasıl enerji elde edildiğidir.

Bu tepkimenin isteği ters dönmesinin sebebi çekirdekte sayısı yükselen pozitif yük sayısıdır. Electrostatik kuvvet nükleer kuvvetten daha zayıf olabilir, ama sayısı daha fazla: demirin çekirdeğinde, her prtoton 25 tane protonu iter, nükleer kuvvet sadece yakındakini tutar.

Ve çekirdek büyüdükçe, bu elektrostatik kuvvet daha önemli hale gelir. plonyum 84 protona ulaştığında, çekirdek(nükleer kuvvet) daha fazla dayanamaz ve protonları radyoaktif bir şekilde hızlıca atar alfa radyoaktivitesinde(helum salınımı), her biri iki proton ve nötron içerir. (Helyum çekirdeği kararlı bir yapıdadır.)Kendi işlevinden dolayı, çekirdeğinde 98 den fazla proton bulunduran elementler dünya üzerinde bulunmazlar

Güneşin birleşim enerjisi

Nükleer enerji devamdaki gibi çalışır: 5 milyar yıl önce yeni Güneş oluştu kütleçekiminin toz bulutlarını uzay tozunu çekmesiyle oluştu, sonrasında Dünya ve diğer gezegenler oluştu. Kütleçekimi güneşi ısıttı Helmholtz'un önerdi şekilde.

Isı enerjisi parçacıklara hız kazandırdı: daha yüksek sıcaklıktaki parçacıklar, daha hızlı parçacıklar ve daha şiddetli çarpışmalar gerçekleşti. Yeni oluşan Güneşin içindeki parçacıkların elektrostatik kuvveti yenecek kadar büyüdüğü zaman ve nükleer kuvvetin etkileyebileceği kadar kısa mesafeye getirdiği zaman nükleer reaksiyonlar gerçekleşmeye başladı ve çekirdek yapışmaya başladı. Bunlar başladıktan sonra hidrojenden deteryum ve sonrasında helyum füzyon edildi. Bu yüksek enerjide gerçekleşen nükleer tepkime şu an güneşin içinde gerçekleşen olayın ta kendisidir,ve ısı gaz basıncını yüksek tutar,yani Güneşi şu anki halinde turae, ve kütleçekim karşısında çökmemesini sağlar. Şu anda Güneşte bir basınç ile çekim arasında bir eşitlik söz konusu..

Farklı nükleer reaksiyonlar Güneşin merkezinde gerçekleşebilir, ki bu proton-proton reaksiyonunu karbon nitrojen döngüsünü de içerir 

Fiziğin bir dalı, kontrol edilen nükleer füzyon, 1950'lerde beri füzyondan enerji üretmeye çalışıyor, bir çeşit su ısıtıcısı gibi buğusunun elektrik enerjisi üretebileceği. Maalesef, hiçbir deneme solar enerjiyi yakalayamıyor: Güneşin büyük kütlesi, ki kütle çok büyük miktarda plazma tutuyor ve merkezinde nükleer füzyon yaratıyor. Bunun yerine fizikçiler büyük manyetik alanlar kullanıyor plazma elde etmek için, ve hidrojenin daha ağır hallerini kullanıyor çünkü çok daha kolay füzyon edilir. Manyetik eşyalar kararsız olabilir ve sıcak ve yoğun olan bir plazma çabucak elden kayıp gidebilir. Usta bir elde bile hapsedilen sadece saniyenin çok kısa bir birimi içinde yok olur.

Çekirdeği birleştirmek

Hisrojenden daha ağır olan hafif çekirdekler daha büyük çekirdeklere ulaştrılıp sonra enerji yayabilir fakat bu enerji hidrojene göre çok daha küçüktür. Yapılan işin enerjisi salınırken, enerji öncelikler protonlara potansiel enerji olarak gelmelidir, Sonrasında protonlar birbirini itecek.[4]

For elements that weigh more than iron (a nucleus with 26 protons), the fusion process no longer releases energy. In even heavier nuclei energy is consumed, not released, by combining similar sized nuclei. With such large nuclei, overcoming the electric repulsion (which affects all protons in the nucleus) requires more energy than what is released by the nuclear attraction (which is effective mainly between close neighbors). Conversely, energy could actually be released by breaking apart nuclei heavier than iron.[4]

Kurşundan daha ağır elementler için, electrik kuvveti çok fazla bazıları pozitif parçalar bırakır, genelliklede alfa parçacıkları(alpha particles). Bu ayrılma radyoaktivitenin bazı davranışlarından biri.

Kurşundan daha ağır elementler için ( bismuth, thorium, uranium, and plutonium hariç) mükemmel derecede hızlı gerçekleşir, ki aslında bunlar bozunumlarlarla(çürüme) ile daha kolay bir şekilde yapılabilir. Genelde daha ağır olan çekirdek daha kolay bozunuma uğrar.[4]

Demirin çekirdeği( demir-56), ve bundan dolayı en kolay enerji kaynağı ondan mümkün olduğunca uzak olan elementlerdir. En hafif olanlar birleştirilebilir—hidrojenin çekirdeği (protonlar)—helyum oluşturmak için, aki bu Güneşin nasıl enerji ürettiğidir. Başka şekilde ağır olanlar hafife doğru parçalanabilir—uranyum veya plütonyumun çekirdeği—daha küçük parçalara, işte bu da nükleer reaktörlerin yaptığı iş.[4]

Nükleer bağ enerjisi 

 ¹²C (karbon 12)nin nükleer bağını oluşturan çekirdeği örnekleyen bir resim ,6 proton ve 6 nötron içermelidir. Protonlar pozitif yüklü ve birbirini iterler fakat nükleer kuvvet bu kuvveti yener ve birbirine yapışır. Nükleer kuvvet kısa mesafeli bir kuvvettir ve uzak mesafelerde işe yaramaz, ve dolayısıyla çekirdeğin dışına hiçbir etkisi yoktur. Nükleer kuvvetler proton ve nötronları bir arada tutar.[5]

The energy of the nucleus is negative with regard to the energy of the particles pulled apart to infinite distance (just like the gravitational energy of planets of the solar system), because energy must be utilized to split a nucleus into its individual protons and neutrons. Mass spectrometers have measured the masses of nuclei, which are always less than the sum of the masses of protons and neutrons that form them, and the difference—by the formula E = m c²—gives the binding energy of the nucleus.[5]

Nükleer füzyon

Helyumun birleşim enerjisi güneşin yakıt kaynağıdır birçok yıldızın olduğu gibi. Güneşin yüzde 74 ü hidrojendir kütlesel olarak). Bu enerji 4 tane proton yani hidrojen çekirdeğinin birleşmesiyle oluşur, bu olayda 2 tane proton 2 nötrona dönüşür.[5]

Bu dönüşüm nükleer kuvvetin(zayıf kuvvet) bir sonucudur. Zayıf kuvvet güçlü kuvvet gibi kısa mesafelerde geçerli fakat uzun mesafelerde başarısız kalır. Zayıf kuvvet proton ve nötronları daha kararlı yapmaya çalışır.40 parçacıktan daha az sayıda parçacıktan oluşan çekirdekler için, bu sayılar genelde eşittir. Proton ve nötronlar genelde çok yakın görünür ve nükleon olarak adlandırılırlar. Atom numarası 209 a yükseldikçe nötronların sayısı sabit kalır fakat protonların sayısı artar bu olay devam eder ta ki nötron ile proton arasındaki oran 2 ve 3 olana kadar.[5]

Protonlar sadece ve sadece yeterli bir enerji( hız)ye sahip olduğunda bir araya gelir. Bu da füzyon sadece yüksek sıcaklıklarda our demektir. Hidrojeni diğer bir hidrojenle bir arada tutmak için gereken koşullar ancak Güneş te var ki bu da orada füzyon olduğunu söylememizdeki şüpheyi tamamen ortadan kaldırır.[5]

Dünyanın okyanusları füzyon yapacak kadar hidrojen içerirler ve burada oluşacak olan ara ürün doğaya zarar vermez ,ve bazıları nükleer enerjinin insanlar için iyi bir kaynak olacağını düşünüyor. Bu konu üstündeki deneyler sadece bir kısımda başarılı oldular. Yeterince hidrojen iyonize edilemedi. Bir teknik yüksek manyetik alan kullanarak yapılıyor çünkü yüklü parçacıklar bu şekilde yönlendirilebilir.Füzyon deneyleri aynı zamanda ağır hidrojende de başarı göstermiş olması güveni arttırıyor. Fakat bu tekniklerle bile yeteri derecede bir başarı sağlanamadı.[5]

Kütle eksiğinin enerjiye dönüşümü

Kütle eksiği çekirdeğin kütlesi ile çekirdeğin oluştuğu maddelerin kütlesinin arasındaki farktır.Kütle eksiği üç etken göze alınarak hesaplanır.[1] Bunlar, çekirdeğin asıl kütlesi,çekirdeği yapısı(proton ve nötronun) ve proton ve nötronun kütlesi. Sonrası eksik kütleyi enerjiye çevirerek devam eder. Ve buna nükller bağ enerjisi denir, fakat bu bir mol atom başına düşen enerji veya bir mol nükleon başına düşen enerji olarak ifade edilmelidir.

Fizyon ve füzyon

Nükleer enerji parçalanarak(fizyon(bölünme) açığa çıkar veya birleşme(füzyon) ile.Bu nükleer enerji kütle enerji eşitliği ile formüle edilir.

ΔE = Δm c²

Burada 

ΔE = kaybolan enerji

Δm =kütle eksiği,

ve c ışık hızı( vakum içinde)

Nükleer enerji ilk olarak fıransız fizikçi Henri Becquerel tarafından 1896 da keşvedilmiştir, [6]

Nükleer kimya simya gibi kullanılabilir örneğin kurşunu altına çevirmek gibi fakat bu çok fazla adımda yapılabilir.Radyoaktif bir çekirdek oluşurken ışıma yapar bunlar alfa ışıması, beta ışıması veya gamma ışıması yapar .Nikel-62, herhangi bir izotopun en yüksek nükleer bağ enerjisini içerir.Eğer ortalama bir düşük nükleer bağ enerjisi olan bir atom daha yüksek bağ enerjisi olan iki atoma dönüştürülürse, enerji kaybeder. Aynı zamanda eğer iki tane yüksek enerji bağı bulunan iki atom daha yüksek bir enerji bağına sahip bir atoma dönüştürülürse yine enerji kaybedilir. Çizelge hidrojenin füzyonunda enerjinin kaybedildiğini gösterir bu durum uranyumun bölünmesinde de görülür. Kararlılık izotoplar arasında değişim gösterir :izotop U-235 , U-238 dan daha kararlıdır.

Nükleer enerji 3 tane egzotermik işlem sonrasında dışarı çıkar:

• Radyoaktif çürüme, Burada nötron ve proton ya parçacık bırakarak ya da elektromanyetik radyasyon, veya ikisi birden. Burası elektromanyetik radyasyon için önemli, bu nükleer bağ enerjinin yükselmesi için önemli değildir. Önemli olan kütlenin artışı. Eğer bir nötron protona dönüşür ve kaybolan enerji 0.782343 MeV (such as rubidium-87 decaying to strontium-87) ise, enerji bağı azalacak demektir .
• Füzyon, iki tane çekirdeğin daha ağır bir çekirdek için birleşmesidir.
• Fizyon ağır bir çekirdeği daha hafif iki veya daha fazla çekirdeği bölmektir.

Atomlar için birleşme enerjisi

Atomun birleşme enerjisi çekirdenkinden farklıdır. İzotopların açıkta kalan enerjisi her zaman için nötr atomun izotopuna göre listelenir ve genelde MeV cinsinden. Sonuç olarak, listelenen kütle açıkları kararlılık için ve izole edilen bir çekirdeğin birleşme enerjisi için bir ölçü değildir. Bunun çok pratiksel sebepleri vardır, çünkü ağır elementleri iyonize etmek çok zordur, başka bir deyişle tüm elektronlarını yok etmek.

Bu uygulama başka sebepler için de uygundur: Kararsız bir çekirdeğin tüm elektronlarını koparmak çekirdeğin yaşam zamanını değiştirir ki bu da çekirdeğin bağımsız bir parça imiş gibi davranılamayacağını gösterir. Bu zaten elektron kapmasından da bellidir.Teorik olarak, ağır atomların modellerinde, elektron kısmen çekirdeğin içinde döner 

Nükleer çürümenin bir çekirdekte yaşanması ona verilen özelliklerin değişmesi demektir. Fizikte kütle açığı olayı birleşme enerjisinin ölçüsü olarak nötr atomun kütle açığı demektir (sadece çekirdek değil) ve atomun kararlılığı üzerine bir ölçüdür. 

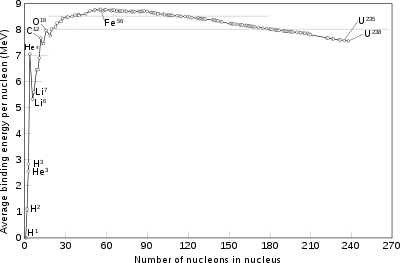
Nuclear binding energy curve

Peryodik tablo elementleri, hidrojenden sodyum da kadar, atomik kütle artışıyla birlikte birleşme enerjisi de artar. Bu artış çekirdekteki her nükleonun kuvvetini arttırarak gerçekleşi, her nükleon diğer bir nükleon tarafından etkilendiği için,daha sıkı bir bağ oluşur çekirdeğin genelinde.

Artan birleşme enerjinin olduğu bölgeyi göreceli bir kararsızlık takip eder magnezyumdan xenona doğru. Bu bölgede, çekirdek nükleer kuvvetlerin artık daha etkileyemeyeceği kadar genişlemiş olur . Aktif nükleer kuvvetler burada ,atomik kütle yüklelirken, elektromanyetik kuvvetler tarafından dengelenmiştir.

Son olarak,xenon dan daha ağır elementler için, atomik kütle artarken birleşme enerjisinde bir azalma görülür. Nükller bölgede, elekromanyetik kuvvetler nükleer kuvvetleri geçmeye başlar.

Birleşim enerjisinin tepesinde , nikel-62 en sıkı bağlanmış çekirdektir sıra demir-58 ve demir-56 ile devam eder.[7] Bu demir ve nikelin neden gezegensel bölgelerde yaygın bulunmasının temel sebebidir, Bu elementler süpernovadan kalıntılardır. Nötronlar yıldızların içinde protona dönüşüp daha fazla enerji salmaya serbest olduğundan dolayı, if the result is a stable nucleus with a larger fraction of protons.Fakat, bu nükleon başına düşen birleşim enerjisi değildir,bu hangi eleentin üretüldiğini control eder. Aslında, ⁶²Ni dan ⁵⁶Fe aışılparçalanmanın aşırı sıcak bir yıldızın içinde mümkün olduğu da iddia edilmişti Sonuç olarak yıldızın içindeki sıcaklık ve basınç dengesi ile tüm madde 56Fe e dönüştürülmüştür.(fakat, en yüksek sıcaklıklarda en düşük enerji seviyesinde olmak zorunda değil) Tabi bu maximum enerji ortamın durumuna uygun olmalıdır, diyelim ki K=298 ve bir atm basıçnötr⁵⁶Fe atomu için—Fakar,bu durumda çekirdek en kararlı ve az enerji seviyesine döner.

Genelde demir-56 nın nikele göre daha yaygın olduğu görüşü kabul görür, Çünkü kararlı nikel-56 14 helyum çekirdeğinin süpernova içinde birleşmesiyle oluşur ,burada demire çürümek için zaman bulamaz yıldızlar arası boşluğa salınmadan önceb.Fakat,nikel-56sonra dan kobalt-56 ya çürür birkaç hafta içinde, sonra bu radyoizotopson olarak demir-56 ya çürür 77.3 gün içinde. bu şekilde oluşan bir radioaktif ışık ikinci tip süpernovadan sonra tespit edilmiştir, örneğin SN 1987A. Bir yıldızın içinde, alfa birleşim işlemi ile nikel 62 oluşturmanın iyi bir yöntemi yoktur.

Birleşim enerjisini ölçmek

En yüksek birleşim enerjisinin ortalama bir çekirdekte bulunması gerçeği farklı karakterde olan kuvvetlerin yarattığı bir sonuçtur. Etkin nükleer kuvvet (strong nuclear force),ki bu proton ve electronları birbirine bağlayan kuvvettir,patlama ile alçalan bir kuvvet sınıfı oluşturur .Fakat iten elektromanyetik kuvvet, mesafe arttıkça düşer. Dört tane diametreden büyük olan çekirdekler daha az sıkı bağlı olurlar fakat çoğu kararlı yapıdadır. Son olarak, 209 dan daha fazla nükleon içeren çekirdekler kararlı olmak için çok büyük olurlar ve çekirdek çürümeye başlar.

Nükleer füzyon en hafif elementleri daha sıkı bağlanan elementlere dönüştürür(örneğin: hidrojen in helyum a çevirmek), ve nükleer füzyon en ağır elementleri daha sıkı bağlı elementlere çevirme işidir(örneğin: uranyumu ve plütonyumu baryum ve Kryptona çevirmek) .iki işlemde enerji yaratır,çünkü ortalama boyuttaki çekirdekler en sıkı bağlı elementlerdir.

Yukarıda görüldüğü gibi deteryum çekirdeğinde, nükleer bağ enerjisi kütle eksiği ile ölçülebilecek kadar geniş, enerji-kütle eşitliğine göre. Atomik bağ enerjisi basitçe nükleonların serbetken bağlandığı zaman kaybolan enerjidir.

Nükleer bağ enerjisi basitçe kütle kaybından hesaplanabilir ve proton ve nötronların kütlelerinin toplamı ile. Eğer kütle farkı biliniyorsa Einstein'ın kütle-enerji( mass-energy equivalence) E = mc² formülü ile kolayca elde edilir. İlk zamanlarda nükleer fizikçiler bu hesaplamaya "packing fraction"(atomik dolgu faktörü) diye adlandırırdı.

Örneğin,atomik kütle birimi (1 u) ¹²C atomunun 12 de biri olarak tanımlanır—fakat hidrojenin atomik kütlesi (proton artı elektron) is 1.007825 u diye biliniyor, bu durumda ¹²C kütlesinin 0.8% ini kaybetmiştir.

Nükleer bağ enerji için yarı deneysel formül

A nükleonları için,A protonunu ve N nötronunu içeren, her nükleon başına düşen bağ enerjisi:

sabitler: ${\displaystyle a=14.0}$; ${\displaystyle b=13.0}$; ${\displaystyle c=0.585}$; ${\displaystyle d=19.3}$; ${\displaystyle e=33}$.

İlk ifade a doygunluk( saturation) olarakadlandırılır ve ilk yaklaşımda bağ enerjisinin her nükleon için aynı olduğunu söyler. ${\displaystyle -b/A^{1/3}}$ yüzey gerilimi etkisidir ve nükleon sayısıyla doğru orantılıdır ; it is largest for light nuclei. ${\displaystyle -cZ^{2}/A^{4/3}}$Coulomb un electrostatik itmesidir; ve Z büyüdükçe daha da önemli olur. ${\displaystyle -d(N-Z)^{2}/A^{2}}$ duruma eşit sayıda bulunduran (nötron ve proton) çekirdeklerin daha kararlı olduklarını söyler. ${\displaystyle \pm e/A^{7/4}}$ tamamen deneyseldir; çift ise + tek ise - işareti alır

A graphical representation of the semi-empirical binding energy formula. The binding energy per nucleon in MeV (highest numbers in dark red, in excess of 8.5 MeV per nucleon) is plotted for various nuclides as a function of Z, the atomic number (y-axis), vs. N, the number of neutrons (x-axis). The highest numbers are seen for Z = 26 (iron).

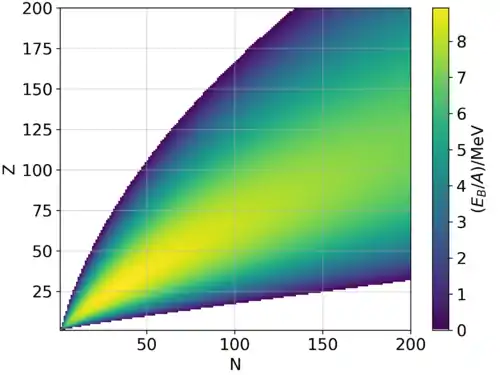
Deneysel olarak elde edilen atomun çekirdek içi kütleleri 

İlerideki tablo bazı kütle açığı endeksinden elde edilen nükleer bağ enerjilerini gösterir[8] 1 u = (931.494028 ± 0.000023) MeV. bağ enerjisini hesaplamak için Z (m_p + m_e) + N m_n - m_nuclideburada Z proton sayısına karşşılık gelir ve N  nötronların sayısına. m_p = 938.2723 MeV, m_e = 0.5110 MeV ve m_n = 939.5656 MeV. A=Z+N. Eğer biz nükleonların sayısının nötronlara eşit olduğunu kabul edersek bu şekilde toplam bağ enerjisini nükleonların bağı ile açıklayabiliriz, ve A nın kütlesini.Başka bir deyişle, bu (Z + N) m_n - mn.na eşit olabilir. Her nükleon başına düşen enerji A ile bölümü ile elde edilebilirdi.

Most strongly bound nuclides atoms

nuclide	Z	N	mass excess	total mass	total mass / A	total binding energy / A	mass defect	binding energy	binding energy / A
56Fe	26	30	-60.6054 MeV	55.934937 u	0.9988372 u	9.1538 MeV	0.528479 u	492.275 MeV	8.7906 MeV
^58Fe	26	32	-62.1534 MeV	57.932276 u	0.9988496 u	9.1432 MeV	0.547471 u	509.966 MeV	8.7925 MeV
^60Ni	28	32	-64.472 MeV	59.93079 u	0.9988464 u	9.1462 MeV	0.565612 u	526.864 MeV	8.7811 MeV
62Ni	28	34	-66.7461 MeV	61.928345 u	0.9988443 u	9.1481 MeV	0.585383 u	545.281 MeV	8.7948 MeV

Some light nuclides resp. atoms

nuclide	Z	N	mass excess	total mass	total mass / A	total binding energy / A	mass defect	binding energy	binding energy / A
n	0	1	8.0716 MeV	1.008665 u	1.008665 u	0.0000 MeV	0 u	0 MeV	0 MeV
^1H	1	0	7.2890 MeV	1.007825 u	1.007825 u	0.7826 MeV	0.0000000146 u	0.0000136 MeV	13.6 eV
^2H	1	1	13.13572 MeV	2.014102 u	1.007051 u	1.50346 MeV	0.002388 u	2.22452 MeV	1.11226 MeV
^3H	1	2	14.9498 MeV	3.016049 u	1.005350 u	3.08815 MeV	0.0091058 u	8.4820 MeV	2.8273 MeV
^3He	2	1	14.9312 MeV	3.016029 u	1.005343 u	3.09433 MeV	0.0082857 u	7.7181 MeV	2.5727 MeV

I

Kaynakça

1. "Nuclear binding energy". How to solve for nuclear binding energy. Guides to solving many of the types of quantitative problems found in Chemistry 116. See: Guides. Purdue University. Temmuz 2010. 16 Kasım 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 10 Temmuz 2010. |eser= dış bağlantı (yardım)
2. "Nuclear Energy". Energy Education is an interactive curriculum supplement for secondary-school science students, funded by the U. S. Department of Energy and the Texas State Energy Conservation Office (SECO). U. S. Department of Energy and the Texas State Energy Conservation Office (SECO). Temmuz 2010. 29 Nisan 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 10 Temmuz 2010.
3. Stern, Dr. David P. (23 Eylül 2004). "Nuclear Physics". "From Stargazers to Starships" Public domain content. NASA website. 9 Nisan 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Temmuz 2010.
4. Stern, Dr. David P. (15 Kasım 2004). "A Review of Nuclear Structure". "From Stargazers to Starships" Public domain content. NASA website. 9 Nisan 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Temmuz 2010.
5. Stern, Dr. David P. (11 Şubat 2009). "Nuclear Binding Energy". "From Stargazers to Starships" Public domain content. NASA website. 9 Nisan 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Temmuz 2010.
6. "Marie Curie - X-rays and Uranium Rays". aip.org. 17 Kasım 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 2006-04-10.
7. Fewell, M. P. (1995). "The atomic nuclide with the highest mean binding energy". American Journal of Physics. 63 (7). ss. 653-658. Bibcode:1995AmJPh..63..653F. doi:10.1119/1.17828.
8. Jagdish K.