Net kuvvet

Fizikte Net Kuvvet, bir cisim üzerine etkiyen kuvvetlerin toplamına eşittir. Net kuvvetin hesaplanması için serbest cisim diyagramı oluşturulur ve ortamdan izole edilerek cisme etkiyen kuvvetler vektörel olarak yazılır. Net kuvvetin cisme olan etkisi net kuvvetin yönüyle aynı olmak zorunda değildir. Bu etkiyi hesaplamak için bileşke kuvvet'in ve tork'un hesaplanması gerekir. Çünkü cisme uygulanan kuvvet tek bir nokta olarak düşünülmeyen cisimlerde bir tork yaratabilir ve bu da bileşke kuvvetin net kuvvetten farklı olmasına sebep olabilir. Kuvvetin cisme etki ettiği nokta göz önünde bulundurularak hesaplanan tork ile beraber net kuvvet bize bileşke kuvveti verir. Ve cisim bileşke kuvvetin öne sürdüğü doğrultuda hareket eder.

Toplam Kuvvet

Toplam kuvvet, ki aynı zamanda net kuvvet ile aynı anlama gelir, cisme etki eden tüm kuvvetlerin toplamına eşittir. Newton’un ikinci yasası'ndan yola çıkarak, bu toplam kuvvetin cisme verdiği ivme kuvvetlerin verdiği toplam ivmelenmeye eşittir.

Kuvvet, vektörel bir büyüklüktür. Bu sebeple bir doğrultusu ve büyüklüğü vardır. Bu özelliği belirtmek için kuvvetin sembolü ${\displaystyle {\vec {F}}}$ olarak gösterilir. Bir vektör yazılırken kuvvetin etkidiği bir A noktası belirtilir ve bir B noktasına kadar ok işareti şeklinde çizilir. Bu ok işareti vektörün yönünü A B noktaları arası mesafe de vektörün büyüklüğünü verir.

Vektör hesaplamaları 1800'lerin sonları ve 1900'lerin başları arasında geliştirilmiştir fakat birazdan bahsedeceğimiz paralelkenar yöntemi'nin Antik Yunanistan'dan kalma olduğu hem Newton hem de Galileo tarafından belirtilmiştir.

Addition of forces

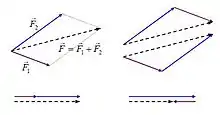
Buradaki diyagramda da görüldüğü üzere vektörel olarak belirtilmiş F₁ ve F₂ kuvvetleri paralelkenar yöntemiyle toplanmıştır. Bunun için kuvvetler paralelkenarın farklı iki kenarı olarak düşünülmüş ve bu paralelkenarın bu iki kuvvetin başlangıç noktasından çıkan kirişi toplam kuvveti vermiştir.

Fakat iki vektörü toplamak veya çıkartmak için bu vektörlerin aynı noktaya uygulanıyor olması gerekir. Kuvvetler de birer vektör olduğu için farklı noktalarına kuvvet uygulanan bir cismin hareketini incelemek için bir nokta belirlenir (genelde kütle merkezi seçilir) ve bu noktaya göre tork alınarak bileşke kuvvet bulunur.

Paralelkenar Kenar Yöntemi

Parallelogram1

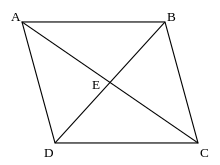
Kuvvet bir vektör olduğu için yönü, büyüklüğü ve bir uygulanma noktası bulunur. Bu kuvvet vektörünü (F) tanımlamak için şu açıklamayı yapabiliriz. Bir A ve B noktası belirleyelim ve bu vektörümüzü Adan B ye bir ok şeklinde çizelim. Ayrıca iki noktayı da uzayda A=(A_x,A_y,A_z) ve B=(B_x, B_y, B_z) olarak tanımlarsak

${\displaystyle F=B-A=(B_{x}-A_{x},B_{y}-A_{y},B_{z}-A_{z})}$

bize F vektörümüzü verir. Bu vektörün büyüklüğü de

${\displaystyle \left|F\right|={\sqrt {(B_{x}-A_{x})^{2}+(B_{y}-A_{y})^{2}+(B_{z}-A_{z})^{2}}}}$

şeklindedir.

Bu aşamadan sonra yapmamız gereken F₁=B-A ve F₂=D-A olarak tanımladığımız kuvvet vektörlerimizde yukarıdaki mantığı uygulamaktır. F₁+F₂ işlemini yapmak için

${\displaystyle F=F_{1}+F_{2}=B-A+D-A}$

yazılabilir ki bu da ayrıca

${\displaystyle F=F_{1}+F_{2}=2\left({\frac {B+D}{2}}-A\right)=2\left(E-A\right)}$

Şeklinde yazılabilir. Burada B ve D noktalarının orta noktası E noktası olduğu için (B+D)/2 işlemi E şeklinde yazılabilir. Ayrıca iki tane E-A bize C-A’yı verir ki bu da bizim vektörlerimizin toplamıdır. Bu uzun işlemleri yapmaktansa düzgünce çizilen iki vektörü, aynılarından karşıya ekleyerek bir paralelkenar oluşturmak ve sonra da bir uçtan diğer uca bir CA doğrusu çizmek bize toplama işlemini yaptıracaktır. İşte bu yönteme paralelkenar yöntemi denir.

Doğrusal ve Dairesel Hareket

Noktasal kuvvet

Bir kuvvet cisme etki ettiğinde, bu tek bir noktadan olur. Bu aşamada kuvvetin etkidiği alan hacimsiz sayılır ve buna noktasal kuvvet denir. Etki ettiği yüzeye de etkime noktası. Fakat gerçek hayatta hacim yok sayılamaz ve kuvvet birkaç farklı noktaya dağılmış şekilde etki eder. Fakat bu cismin dönme hareketini incelerken sorunlara yol açabilir ve bunun giderilmesi için aşağıdaki maddelerle çözümlenir.

Genellikle kuvvetin uygulandığı alan cisme göre ufak kalır ve bu nedenle yaklaşık bir nokta belirlenir ve bu varsayım üzerinden işlemler yapılır. Hata payının yüksek çıkıp çıkmadığı kolaylıkla saptanabilir.

Eğer kuvvetin uygulandığı alan bir varsayım yapacak kadar küçük değilse veya bütün parçacıklara uygulanıyorsa(yerçekimi kuvveti gibi), o zaman işlem bütün parçacıklar için tek tek yapılır. Bunun için diferansiyel denklemler ve integral matematiği kullanılır. Düzgün yerçekimsel kuvvet gibi çok nadir durumlarda ise cisim tek bir noktaya indirgenerek işlem yapılabilir. Her hangi işlemler uygulanacak olursa olsun, katı cisimlerdeki problemlere yaklaşımda ilk olarak kuvvetlerin gösterildiği bir model, noktasal kuvvet modeli, çizilir.

Katı Cisimler

Free body acceleration

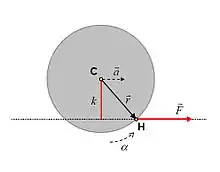
Bu örnekte sahip olduğumuz bir F kuvveti H noktasından cisme etki ediyor. C noktasını cismin merkezi farz edersek ve cismin m kütlesinde olduğunu var sayarsak buradan cismin merkezinin ivmesi

${\displaystyle {\vec {a}}={\frac {\vec {F}}{m}}}$

Ve cismin açısal ivmesi de

${\displaystyle {\vec {\alpha }}={\frac {\vec {T}}{I}}}$

olarak karşımıza çıkar. Buradaki ${\displaystyle {\vec {T}}}$, tork ve I ise eylemsizlik momentidir. Buradaki torkun kuvvetle olan bağıntısı ise

${\displaystyle {\vec {T}}={\vec {r}}x{\vec {F}}}$

şeklindedir. Buradaki ${\displaystyle {\vec {r}}}$ pozisyon vektörü olup şekilde de gözüktüğü gibi cismin merkezinden kuvvetin uygulandığı etkileşim noktasınadır.

Tork vektörü uygulanan kuvvete ve aynı zamanda da pozisyon vektörüne diktir. Ancak hangi yöne olduğunu bulmak için sağ el kuralı uygulanmalıdır. Bu örnekte tork vektörü kâğıttan dışarı, gözlemciye doğrudur.

Eylemsizlik momenti de cismin merkezinden geçen ve aynı zamanda da tork vektörüne paralel olan bir doğru çizilerek bulunur. Cisimlerin şekilleri ve kütleleriyle doğrudan alakalıdır.

Bileşke Kuvvet

Katı cisimlerin hareketini incelerken bakılması gereken iki şey bileşke kuvvet ve tork'tur. Ama nadiren de olsa tork sıfır olabilir. Buna torksuz bileşke denir.

Rezultanta

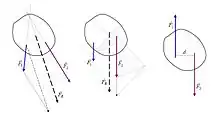
1.Şekilde bileşke kuvvet bulmak için bu iki kuvvettin birleşme noktaları hesaba katılır. Örnekte olduğu gibi birleşebilen bu kuvvetin bileşkesi paralelkenar yöntemiyle rahatlıkla bulunabilir. Bu yöntemdeki amaç ortak kesişim noktasını gözlem noktası almaktır. Bu sayede tork her zaman sıfırdır ve bu sayede bileşke kuvvet net kuvvete eşittir.

2.Şekilde ise birbirine paralel iki kuvvetin bileşkesi alınmakta. Bu iki kuvvet paralel oldukları için direkt olarak birbirlerinin üzerine eklenerek işlem yapılabilir. Buradaki tork sorunu ise kuvvetlerin paralel ve aynı yönlü olması sayesinde kendiliğinden çözülür. Gözlem noktası farkı olmadan tork sıfıra eşittir.

3. Şekilde ise kuvvetler farklı zıt yönlü ve eşit büyüklükte olduğu için net kuvvet sıfıra eşittir. Fakat bu örnekte tork mevcuttur ve ${\displaystyle T=Fd}$ formülü ile bulunabilir.

Kullanım

Genel olarak bir sisteme etki eden kuvvet bir net kuvvet ve ona bağlı bir tork ile ifade edilebilir. Bunun için yukarıda bahsedilen çözümler uygulanabilir. Burada açıklanmış durumun aksine bazı yazılarda net kuvvet ve bileşke kuvvetin eş anlamlı olarak kullanıldığının da altından geçmek gerekir.