Planck yasası

Planck yasası belirli bir sıcaklıkta termal denge durumunda bulunan bir kara cisim ışımasının yaydığı elektromanyetik radyasyonu ifade eder. Yasa 1900 yılında Max Planck bu ismi önerdikten sonra isimlendirilmiştir. Planck yasası modern fiziğin ve kuantum teorisinin öncül bir sonucudur. 

Planck yasası (renkli eğriler) kara cisim ışımasının ve ultraviyole dönüm noktasının (siyah eğri) kesin olarak bir ifade şeklidir.

Herhangi bir yüzeyin spektral radyansı, ${\displaystyle B_{\nu }}$, farklı frekansların ne kadar enerji yaydığının bir ifade şeklidir. Yüzeyin birim alanına, üzerinde radyasyonun ölçümü yapılabilen bir katı bir cismin açısına ya da birim frekansından yayılan güce göre ölçülür. Planck, T ile gösterilen belirli bir sıcaklıktaki cismin spektral radyasyonunun şu şekilde olduğunu gösterdi:

Burada k_B Boltzmann sabiti, h the Planck sabiti, and c ışığın ortamdaki hızını (vakumda ya da herhangi bir materyalde olabilir) ifade eder.[1][2][3] Spektral radyans ayrıca birim frekans yerine birim dalga boyuna göre de ölçümlenebilir. Bu durumda olayın matematiksel tanımı şu hali alır:

${\displaystyle B_{\lambda }(\lambda ,T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\mathrm {B} }T}}-1}}}$.

Uluslararası birim sistemine göre W·sr⁻¹·m⁻²·Hz⁻¹ B_ν'nin ve W·sr⁻¹·m⁻³ ise B_λ'nin birimidir. Planck yasası bu birimler dışında ayrıca belirli bir dalga boyunda yayılan foton sayısına göre ya da yayılan radyasyonun bir hacimdeki enerji yoğunluğuna göre de ifade edilebilir. 

Planck yasası yüksek frekanslarda (yani düşük dalga boylarında) Wien yaklaşımı uygulamaya eğilimliyken, düşük frekanslarda (yani yüksek dalga boylarında) Rayleigh–Jeans yasası kullanılmaya eğilimlidir.  

Max Planck bu yasayı 1900 yılında yalnızca ampirik olarak karar verilmiş sabitler kullanarak geliştirdi. Ancak daha sonra bunların termodinamik denge halindeki radyasyon için özel durumda kararlı bir enerji dağılımı olarak ifade edilebileceğini gösterdi.[4] Bir enerji dağılımı olarak bu durum, Bose–Einstein dağılımı, Fermi–Diracdağılımı ve Maxwell–Boltzmanndağılımını içeren termal denge ailesi dağılımlarından biridir.

Giriş

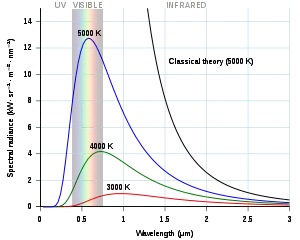
Her fiziksel cisim kendiliğinden ve devamlı olarak elektromanyetik radyasyon yayar. Termodinamik denge durumu yakınındayken yayılan radyasyon da Planck yasasıyla ifade edilebilir. Sıcaklığa bağımlılığı sebebiyle Planck radyasyonuna termal diyebilmek mümkündür. Bir cismin sıcaklığı yükseldikçe her dalgaboyunda daha çok radyasyon yayar. Planck radyasyonu maksimum şiddetine sıcaklığına bağlı olarak özel bir dalga boyunda ulaşır. Örnek verecek olursak, oda sıcaklığında (~300 K) bulunan bir cisim genellikle kızılötesi veya görülemeyen dalga boyunda termal radyasyon yayarlar. Sıcaklık arttıkça kızılötesi radyasyon miktarı artarken aynı zamanda ısı olarak hissedilebilir ve cisim görülebilir bir şekilde kırmızı bir parıltı yayar. Daha yüksek sıcaklıklarda bir cisim göz kamaştırıcı şekilde sarı ya da mavi-beyaz parıldayabilir ve yüksek miktarda ultraviyole ve x-ray dalga boylarını bile içine alan kısa dalga boylarında radyasyon yayar. Güneş'in yüzeyi (~6000 K) yüksek miktarda hem kızılötesi hem de ultraviyole ışık yayar ve bu yayılımlar görülebilir spektrumda maksimum değerine ulaşılar. 

Fiziksel medyumun içerisinde radyasyon madde tarafından emilebilir ve yayılabilir. Bu durum enerjinin ısı olarak transfer edilmesine aracı olabilir ve maddenin iç enerjini değiştirebilir. Ayrıca farklı durumlarda bulunan moleküllerin sayısını da değiştirebilir.

Termal denge durumunda en yüksek miktardaki  radyasyon olan Planck radyasyonu herhangi bir cismin kimyasal bilişimi ya da yüzey yapısı nasıl olursa olsun yüzeyden yayılan radyasyondur. Radyasyonun medya arasındaki bir ara yüzeyi boyunca radyasyon geçişi arayüz emisyonu ile karakterize edilebilir. Geçen radyasyonun radyansı Planck radyansına bölünerek bulunur. Bu da genellikle radyasyonun kimyasal bileşimine, fiziksel yapısına, sıcaklığına, dalgaboyuna, faz açısına ve polarizasyona bağlı olarak değişir.[5] Bir ara yüzeyin radyasyonunun yayılabilirliği ayrıca onun transmitansı ya da absorbansı olarak bilinir. Doğal bir ara yüzeyin bu yayılabilirliği daima sıfır ile bir arasındadır. Bir ara yüzeyin yayılabilirliğinin ve yansıtabilirliğinin toplamı bire eşittir. Yani mükemmel bir yansıtma özelliğine sahip bir ara yüzeyin yayılabilirliği sıfırken, yansıtabilirliği birdir. Mükemmel olarak yayılabilme özelliğine sahip ara yüzeyler içinse yansıtabilirlik sıfırken yayılabilirlik bire eşittir. 

Yayılabilirliği bir olan başka bir medyum ile arayüzeyi olan ve bütün radyasyonu kendi içine absorbe eden cisimler kara cisim olarak adlandırılabilir. Kara bir cismin yüzeyi, herhangi bir dalga boyunda mükemmel olarak yansıtamayan bir katı ve opak duvar ile birlikte sıcaklığı sabit kalan büyük bir duvarla çevrelenmiş bir duvardaki küçük bir delik olarak modellenebilir. Denge durumundayken bu duvarın içindeki radyasyon Planck yasası ile izlenebilir. Bu radyasyon delikten dik bir açıyla yayınlan radyasyon olarak iyi örneklendirilmiştir.

Tıpkı Maxwell-Boltzmann dağılımı gibi belirli bir sıcaklıktaki termodinamik denge durumunda birçok korunmuş masif parçacık için özel bir maksimum entropi enerji dağılımı vardır ve sıfır kütleye sahip korunmayan bu fotonların gazı bir Planck dağılımıdır.[6][7] Kütlelerin ve kaç tane parçacık bulunduğunun bir rol oynadığı gaz materyalinin aksine, spektral radyans, denge durumundaki bir foton gazının enerji yoğunluğu ve basıncı tamamıyla sıcaklığa göre karar verilir. Eğer foton gazı başlangıçta Planckian değilse termodinamiğin ikinci yasasına göre fotonlar ve diğer parçacıklar arasında ya da fotonların kendi arasındaki etkileşimi bile Planck dağılımını değiştirmek ve yaklaşmak için foton enerji dağılımına sebep olabilirler. Termodinamik dengedeki fotonlara böyle bir yaklaşım muhtemel denge durumundaki bir sıcaklıkta bulunan, doğru sayıda ve doğru enerjide saptanan Planck dağılımındaki boşlukları doldurmak için oluşturulabilir ya da imha edilebilirler.

Türetimi

Bir köşesinin uzunluğu L olan T sıcaklığında termal denge durumunda bulunan elektromanyetik radyasyon ile dolu iletken duvarlarla oluşan bir küp düşünün. Eğer duvarlardan birinde küçük bir delik bulunuyorsa bu delikten yayılan radyasyon kara cismin karakteristik özelliklerini mükemmel bir şekilde taşıyacaktır. Biz öncelikle bir boşluğun içindeki spektral enerji yoğunluğunu hesaplayacağız ve ondan sonra ise yayılan radyasyonun spektral radyansına karar vereceğiz.

Kübün duvarlarında elektrik alanın paralel bileşenleri ve manyetik alanın ortogonal bileşinlerinin kesinlikle sıfırlanması gerekir. Bir kutuda bulunan yalnız bir parçacığın dalga fonksiyonuna benzer bir şekilde manyetik alanın ve elektrik alanın periyodik fonksiyonun süperpozisyonda olduklarını söyleyebiliriz. Duvarlara ortogonal olan üç yöndeki üç adet dalga boyu λ₁, λ₂ ve λ₃ şu şekilde olacaktır.

${\displaystyle \lambda _{i}={\frac {2L}{n_{i}}},}$

Formüldeki n_i bir tam sayıyı ifade etmektedir. Her bir n_i kümesi için birbirinden bağımsız iki tane liner çözüm bulunur(modlar). Kuantum teorisine göre bir modun enerji seviyeleri şu şekilde formülize edilebilir:

${\displaystyle E_{n_{1},n_{2},n_{3}}\left(r\right)=\left(r+{\frac {1}{2}}\right){\frac {hc}{2L}}{\sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}.\qquad {\text{(1)}}}$

Bir kuantum numarası olan r moddaki foton sayısını ifade eder şeklinde yorumlayabiliriz. Her bir n_i kümesi için bulunan iki mod spini 1 olan fotonların iki polarizasyon durumuna karşılık gelmektedir. Buradaki önemli noktalardan biri de r = 0 için modun enerjisi sıfır değildir. Elektromanyetik alanın bu vakum enerjisi Casimir etkisi nden sorumludur. Devam eden işlemlerde T gibi belirli bir sıcaklıkta bulunan bir kutunun iç enerjisini hesaplayacağız.

İstatiksel mekanik göz önünde bulundurulduğunda, belirli bir modun enerji seviyeleri üzerindeki olasılıksal dağılımı şu şekilde formülize edilir:

${\displaystyle P_{r}={\frac {\exp \left(-\beta E\left(r\right)\right)}{Z\left(\beta \right)}}.}$

Burada,

${\displaystyle \beta \ {\stackrel {\mathrm {def} }{=}}\ 1/\left(k_{\mathrm {B} }T\right).}$

Paydadaki Z(β), yalnız bir modun bölüşüm fonksiyonunu ifade eder ve P_r düzgün bir şekilde normalize edilir:

${\displaystyle Z\left(\beta \right)=\sum _{r=0}^{\infty }e^{-\beta E\left(r\right)}={\frac {e^{-\beta \varepsilon /2}}{1-e^{-\beta \varepsilon }}}.}$

Burada dolaylı olarak tanımlama yapılmıştır

${\displaystyle \varepsilon \ {\stackrel {\mathrm {def} }{=}}\ {\frac {hc}{2L}}{\sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}},}$

ve tek bir fotonun enerjisidir. Bir moddaki ortalama enerji bölüşüm fonksiyonu ile ifade edilebilir:

${\displaystyle \left\langle E\right\rangle =-{\frac {d\log \left(Z\right)}{d\beta }}={\frac {\varepsilon }{2}}+{\frac {\varepsilon }{e^{\beta \varepsilon }-1}}.}$

İlk vakum enerjisi terimi dışında bu formül Bose-Einstein istatistiğine göre tanımlanabilen parçacıklar için genel formüle nazaran özel bir durumdur. Bunun nedeni ise fotonun toplam sayısında herhangi bir kısıtlamanın olmamasıdır, yani kimyasal potansiyelinin sıfır olmasıdır.

Eğer biz enerjiyi yerel duruma göre ölçersek, kutudaki toplam enerji ${\displaystyle \scriptstyle {\left\langle E\right\rangle }-{\frac {\varepsilon }{2}}}$ bütün tek foton durumlarının toplamıyla bulunur. Bu işlem aynı zamanda aynı şekilde termodinamik limitte L sonsuza yaklaşırken de yapılıp çözüme ulaşılabilir. Bu limitte ε sürekli olur ve sonrasında ${\displaystyle \scriptstyle {\left\langle E\right\rangle }-{\frac {\varepsilon }{2}}}$ ifadesinin belirlediğimiz parametre üzerinden integrali alınır. Bu yolla kutudaki toplam enerjiyi hesaplamak için verilen enerji aralığında kaç tane foton olduğunu bilmemiz gerekir. Eğer enerjisi ε ve ε + dε böylece g(ε)dε, burada g(ε) yoğunluğu (belirli bir anda hesaplayabileceğimiz) ifade eder. Sonuç olarak:

${\displaystyle U=\int _{0}^{\infty }{\frac {\varepsilon }{e^{\beta \varepsilon }-1}}g(\varepsilon )\,d\varepsilon .\qquad {\mbox{(2)}}}$

Yoğunluğu hesaplamak için denklemi (1) yeniden aşağıdaki gibi yazarız:

${\displaystyle \varepsilon \ {\stackrel {\mathrm {def} }{=}}\ {\frac {hc}{2L}}n,}$

burada n norm vektörüdür n = (n₁, n₂, n₃):

${\displaystyle n={\sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}.}$

Her n vektörünün tam sayı bileşeninin büyük ya da sıfıra eşit olduğu koşulda iki foton durumu vardır. Bunun anlamı belirli bir n-uzayda bölgesindeki toplam foton sayısının bu bölgedeki hacimden iki kat daha fazla olduğudur. dε şeklinde bir enerji aralığı n-uzayda dn = (2L/hc)dε kalınlığındaki bir kabuğa tekabül eder. Bu kabuk bir kürenin oktantına yayılır çünkü n bileşenleri pozitif olmak zorundadır. Foton sayısı g(ε)dε, bir enerji aralığında dεyi ifade eder. Böylece:

${\displaystyle g(\varepsilon )\,d\varepsilon =2{\frac {1}{8}}4\pi n^{2}\,dn={\frac {8\pi L^{3}}{h^{3}c^{3}}}\varepsilon ^{2}\,d\varepsilon .}$

Bunu denklem (2)'de yerine koyarsak elde edeceğimiz formülizasyon şudur:

${\displaystyle U=L^{3}{\frac {8\pi }{h^{3}c^{3}}}\int _{0}^{\infty }{\frac {\varepsilon ^{3}}{e^{\beta \varepsilon }-1}}\,d\varepsilon .\qquad {\text{(3)}}}$

Bu denklemden herhangi biri spektral enerji yoğunluğunu frekansının bir fonksiyonuymuş ${\displaystyle u_{\nu }(T)}$ gibi ve bir dalga boyu fonksiyonuymuş u_λ(T) gibi türetebilir:

${\displaystyle {\frac {U}{L^{3}}}=\int _{0}^{\infty }u_{\nu }(T)\,d\nu ,}$

burada:

${\displaystyle u_{\nu }(T)={8\pi h\nu ^{3} \over c^{3}}{1 \over e^{h\nu /k_{\mathrm {B} }T}-1}.}$

Ve:

${\displaystyle {\frac {U}{L^{3}}}=\int _{0}^{\infty }u_{\lambda }(T)\,d\lambda ,}$

burada:

${\displaystyle u_{\lambda }(T)={8\pi hc \over \lambda ^{5}}{1 \over e^{hc/\lambda k_{\mathrm {B} }T}-1}.}$

Bu aynı zamanda birim hacimdeki birim dalga boyunun enerjisinin birimiyle beraber bir spektral enerji yoğunluğu fonksiyonunu ifade eder. Bose ve Fermi gazları için bu tip integraller polilogaritmalarla ilgili olarak ifade edilebilirler. Ancak bu durumda, yalnızca temel fonksiyonları kullanarak kapalı formdaki integrali hesaplamak mümkün olmaktadır. Böylece:

${\displaystyle \varepsilon =k_{\mathrm {B} }Tx,}$

Denklem (3) integrasyonu boyutsuz bir şekilde aşağıdaki gibi yapar:

${\displaystyle u(T)={\frac {8\pi (k_{\mathrm {B} }T)^{4}}{(hc)^{3}}}J,}$

buradaki J aşağıda verildiği üzere bir Bose–Einstein integrali'dir:

${\displaystyle J=\int _{0}^{\infty }{\frac {x^{3}}{e^{x}-1}}\,dx={\frac {\pi ^{4}}{15}}.}$

Kutunun içerisindeki toplam elektromanyetik enerji böylelikle şu hali alır:

${\displaystyle {U \over V}={\frac {8\pi ^{5}(k_{\mathrm {B} }T)^{4}}{15(hc)^{3}}},}$

burada V = L³ kutunun hacmini ifade eder.

hc/k_B kombinasyonu 14 387.770 μm·K değerindedir.

Bu bir Stefan-Boltzmann yasası (birim zamanda birim yüzeye kara cisim tarafından yansıtılan toplam enerjiyi ifade eder) değildir ama Stefan–Boltzmann sabiti σ kullanılarak aşağıdaki gibi daha öz bir şekilde yazılabilir:

${\displaystyle {U \over V}={\frac {4\sigma T^{4}}{c}}.}$

4σ/c sabiti bazen radyasyon sabiti olarak ifade edilir.

Küçük delikten çıkan radyasyonun spektral radyansı aşağıdaki gibidir çünkü radyasyon bütün yönlerde birbirine eşittir ve ışık hızında (c) yayılır.

${\displaystyle B_{\nu }(T)={\frac {u_{\nu }(T)\,c}{4\pi }},}$

buradan

${\displaystyle B_{\nu }(T)={\frac {2h\nu ^{3}}{c^{2}}}~{\frac {1}{e^{h\nu /k_{\mathrm {B} }T}-1}}.}$

Dalga boyu birimindeki B_λ(T) için bu formülizasyon ${\displaystyle \nu }$ ifadesi yerine c/λ koyularak ve hesaplanarak başka bir ifade şekline dönüştürülebilir:

${\displaystyle B_{\lambda }(T)=B_{\nu }(T)\left|{\frac {d\nu }{d\lambda }}\right|.}$

Unutulmamalıdır ki boyutsal analiz yukarıdaki denklemin sol tarafındaki paydadaki steradyanın birimini gösterir. Bu birim türetim sürecinde oluşturulmuş ve bitene kadar devam etmiştir ancak denklemin sol tarafındaki parçası için hiçbir boyutun hiçbir parçasında yoktur.

Bu türetme Brehm & Mullin'in 1989 yılındaki çalışmalarına dayanmaktadır.

Kaynakça

1. Planck 1914, pp. 6, 168
2. Chandrasekhar 1960, p. 8
3. Rybicki & Lightman 1979, p. 22
4. Planck 1914, p. 42
5. Hapke 1993, pp. 362–373
6. Planck 1914
7. Loudon 2000, pp. 3–45