Rastgele sarım

Düzensiz sarım veya rastgele sarım (İngilizce random coil), monomerlerin rastgele doğrultulu olup buna rağmen bitişik olanların birbirine bağlı oldukları bir polimer konformasyonudur. Belli bir şekil değil, bir makromolekül topluluğundaki tüm şekillerin istatistik bir dağılımıdır. Bu konformasyonun adının arkasında yatan kavram, spesifik, stabilize edici bir etkileşim olmayınca, polimer omurgasının tüm konformasyonları rastgele "örnekleyeceğidir". Çözelti halinde, veya ergime sıcaklığının üzerinde olan, çoğu doğrusal, dalsız homopolimer, (yaklaşık) rastgele sarım şeklini alır. Birbirine eşit uzunlukta olmayan monomerlere sahip kopolimerler dahi rastgele sarım dağılımı gösterir, eğer altbirimler arasında spesifik etkileşim yoksa. Dallı polimerlerin parçaları da rastgele sargı şekli alabilir.

Ergime sıcaklığının altında çoğu termoplastik polimer (polietilen, naylon, vs.), zincirlerin yaklaşık rastgele sargı oldukları amorf bölgeleri vardır, bu bölgeler arasında kristalin bölgeler yer alır. Amorf bölgeler elastiklik sağlar, kristalin bölgeler dayanıklılık ve sertlik sağlar.

Protein gibi daha karmaşık polimerlerde omurgaya bağlı ve birbiri ile etkileşen çeşitli kimyasal gruplar vardır. Proteinler iyi tanımlı yapılar hâlinde özbirleşir. Ancak proteinlerin bazı kısımlarınin ve ikincil yapıdan mahrum polipeptitlerin rastgele sarım konformasyonuna sahip olduğu varsayılır, yani birbirine bitişik amino asit kalıntıları arasındaki tek sabit ilişki, bunların birbirlerine bir peptit bağı ile bağlı olmasıdır. Gerçekte durum böyle değildir, çünkü amino asit yan zincirleri arassındaki etkileşimler toplulukta enerji ağırlıklı bir dağılım yaratacktır, düşük enerjili konformasyonlar daha sık mevcut olacaktır. Ayrıca, rastgele amino asit dizileri dahi bir miktar hidrojen bağlanması ve ikincil yapı gösterir. Bu nedenle, "istatistik sarım" terimi bazen tercih edilir. Rastgele sarım hâli ile ilişkili olan konformasyonal entropi onun enerji stabilizasyonuna önemli derecede katkıda bulunur ve protein katlanmasına engel teşkil eden enerji bariyerinin büyük bölümünden sorumludur.

Proteinlerdeki rastgele sarım konformasyonu spektroskopik yöntemlerle tespit edilebilir. Düzlemsel amit bağının düzeni, dairesel dikroizmde ayırdedici bir sinyale neden olur. Rastgele sarım konformasyonundaki amino asit kalınıtılarının kimyasal kayması nükleer manyetik rezonansta iyi bilinir. Bu tanımlayıcı sinyallerden sapma olması genelde bir miktar ikincil yapı olduğunun işareti sayılır. Ayrıca, çok boyutlu NMR deneyleriyle gözlemlenebilen, birbirine komşu amino olmayan amino asitler arasındaki etkileşimler, rastgele sarım konformasyonuna sahip peptitlerde görülmez. Benzer şekilde, kristalografi deneylerinde rastgele sarım parçaları "elektron yoğunluğu" veya kontrastta azalmaya neden olur. Bir polipeptit zinciri için rastgele sarım hâli, sistemin denatürasyonu ile elde edilebilir. Ancak, denatüre olsalar dahi, proteinlerin hiçbir zaman gerçek anlamda rastgele sargı olmadıklarına dair kanıtlar mevcuttur (Shortle & Ackerman).

Rastgele yürüme modeli: Gauss zinciri

Kısa rastgele zincir

Bir zincirin nispeten kompakt şekilde sarılabileceği muazzam sayıda, ama az veya çok gergin olduğu nispeten az sayıda farklı yol vardır. Her konformasyonun eşit olasılığı veya istatistik ağırlığı varsa, zincirlerin yumak şekilli olma olasılığı uzamış durumda olmalarından çok daha muhtemeldir. Dolayısıyla, bir zincirler topluluğundaki zincirlerin çoğu gevşek bir yumak top gibi olacaktır. Onlardan herhangi birinin çoğu zaman sahip olacağı şekil bu olacaktır.

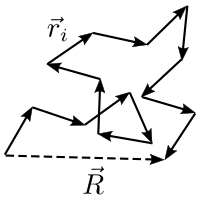
Doğrusal bir polimerin, N altbirimli ve özgür eklemli bir zincir olduğunu varsayalım, her altbirim $\scriptstyle \ell$ uzunlukta ve zero hacimli olsun, öyle ki zincirin hiçbir bölümü bir diğerini herhangi bir konumdan dışlayamasın. Böylesi bir zincirin parçalarının üç boyut içinde bir rastgele yürüyüş (daha doğrusu "rastgele uçuş") yapıyor olarak düşünebiliriz. Bu ideal zincir matematik modelidir. Zincirin iki ucu arasındaki en büyük uzaklık L, $\scriptstyle N\,\times \,\ell$ 'dir. Her zincir konformasyonun eşit istatistiksel ağırlığı olduğunu varsayarsak, uçlar arasındaki uzaklığın r olma olasılığı P(r)'nin

P(r)={\frac {4\pi r^{2}}{(2/3\;\pi \langle r^{2}\rangle )^{3/2}}}\;e^{-\,{\frac {3r^{2}}{2\langle r^{2}\rangle }}}

denklemi ile tarif edilen bir karakteristik bir dağılıma uyacağı gösterilebilir. Zincirin uçları arasındaki ortalama ortalama karekök uzaklık, $\scriptstyle {\sqrt {\langle r^{2}\rangle }}$ , $\scriptstyle \ell$ çarpı N 'nin kareköküdür. Bir diğer deyişle, ortalama uzaklık N^0.5 ile ölçeklenir.

Bu modelin "Gauss zinciri" olarak adlandırılmasına rağmen, dağılım fonksiyonu bir gauss (normal( dağılım değildir. Bir Gauss zinciri için uçtan uca uzaklık olasılık dağılım fonksiyonu sadece r > 0 için sıfırdan farklıdır.[1]

Gerçek polimerler

Gerçek bir polimer özgür eklemli değildir. Bir -C-C- bağının 109,5 derecelik sabit bir tetrahedral açısı vardır. L değeri tamamen uzatılmış bir polietilen veya naylon için iyice tanımlıdır ama N x l 'den daha kısadır, omurganın zigzag şeklinden dolayı. Ancak pek çok zincir bağı etrafında serbest rotasyon vardır. Yukarıdaki model geliştirilebilir. Daha uzun, "effektif" bir birim uzunluk ve daha küçük bir N tanımlanabilir, öyle ki, zincir özgür eklemli gibi değerlendiirlebilir ve L = N x l kısıtı geçerliliğini korumaktadır. Bu zincir de Gauss dağılımı gösterir. Ancak, özel durumlar da hatasız olarak hesaplanabilir. Özgür rotasyonlu (özgür eklemli değil) polietilen (her -C-C-'nin bir altbirim sayıldığı polimer) için ortalama uçtan uca uzaklık l çarpı 2N 'nin kareköküdür, yani 1,4 kat bir artmadır. Rastgele yürüme hesaplamasında varsayılan sıfır hacimden farklı olarak, tüm gerçek polimerlerin parçaları uzayda yer işgal ederler, atomlarının van der Waals yarıçapları ve bağ rotasyonuna engel olan cüsseli fonksiyonel gruplar nedeniyle. Hesaplamalarda bunlar da göz önüne alınabilir. Bu etkilerin hepsi uçlar arası ortalama mesafeyi artırır.

Polimerizasyon rassal (stokastik) olarak ilerlediği için, gerçek bir sentetik polimer topluluğundaki zincir uzunlukları istatistik dağılım gösterir. Bu durumda N değerini ortalama bir değer olarak saymalıyız. Ayrıca, çoğu polimerden rastgele oluşan dallanmalar olur.

Rastgele yürüyüş modeli, yerel kısıtlar için düzeltmeler ile dahi, zincirler arasındaki, ve aynı zincirin uzak kısımları arasındaki, enterferans olgusunu göz ardı eder. Bir zincir çoğu zaman belli bir konformasyondan ona çok benzer başka bir konformasyona geçiş yapamaz çünkü zincirin bir kısmının başka bir kısmının içinden veya komuşu bir zincirin içinden geçmesi gerekir. Bu yetersizliklerine rağmen, ideal-zincir, rastegele-sarım modeli, çözelti içindeki ve amorf hâldeki gerçek polimerlerin şekil ve büyüklüklerinin hiç olmazsa nitel bir göstergesi olduğu kabul edilebilir, zinciri oluşturan monomerler arasındaki fizikokimyasal etkileşimler zayıf oldukça. Bu model, ve Flory-Huggins Çözelti Theorisi,[2][3] (Paul Flory 1974'te bunun için Nobel Kimya Ödülü'nü almıştır) sözde sadece ideal, derişik çözeltiler için geçerlidir. Ama dışlanmış hacim etkilerinin birbirini götürüyor olabileceğine dair bulgular vardır (örneğin, nötron kırınımı çalışmalarından), öyle ki, bazı şartlarda, amorf polimerlerdeki zincir boyutları yaklaşık ideal, hesaplanmış boyutlara sahip olabilir.[4] Farklı zincirler kooperatif olarak etkileştiğinde, örneğin katı termoplastiklerin kristalin bölgelerinin oluşumunda, farklı bir matematiksel model kullanılmalıdır.

Sert polimerler, sarmal peptitler, Kevlar ve çift iplikli DNA gibi, solucan benzeri zincir modeli ile değerlendirilebilir.

Ayrıca bakınız

Protein katlanması
Doğal hâl
Ergimiş globül
Olasılık teorisi

Kaynakça

Aslında, gerşek zincirler için Gauss zincirinin dağılım fonksiyonu fiziksel değildir, çünkü uzatılmış zincirden daha büyük uzunluklar için dahi sıfır olmayan olasılıkları vardır. Bunun nedeni, bu formülün ancak sonsuz uzunlukta zincir durumu için geçerli olmasıdır. Ancak bu olasılıklar çok küçük oldğu için pratikte bu sorun yaratmaz.
Flory, P.J. (1953) Principles of Polymer Chemistry, Cornell Univ. Press, ISBN 0-8014-0134-8
Flory, P.J. (1969) Statistical Mechanics of Chain Molecules, Wiley, ISBN 0-470-26495-0; reissued 1989, ISBN 1-56990-019-1
"Conformations, Solutions, and Molecular Weight" from "Polymer Science & Technology" courtesy of Prentice Hall Professional publications 9 Mart 2008 tarihinde Wayback Machine sitesinde arşivlendi.

Dış bağlantılar

polymer statistical mechanics (İngilizce)
A topological problem in polymer physics: configurational and mechanical properties of a random walk enclosing a constant are (İngilizce)
D. Shortle and M. Ackerman, Persistence of native-like topology in a denatured protein in 8 M urea, Science 293 (2001), pp. 487–48930 Eylül 2007 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce)
Sample chapter "Conformations, Solutions, and Molecular Weight" from "Polymer Science & Technology" courtesy of Prentice Hall Professional publications4 Ağustos 2004 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Aslında, gerşek zincirler için Gauss zincirinin dağılım fonksiyonu fiziksel değildir, çünkü uzatılmış zincirden daha büyük uzunluklar için dahi sıfır olmayan olasılıkları vardır. Bunun nedeni, bu formülün ancak sonsuz uzunlukta zincir durumu için geçerli olmasıdır. Ancak bu olasılıklar çok küçük oldğu için pratikte bu sorun yaratmaz.

[2] Flory, P.J. (1953) Principles of Polymer Chemistry, Cornell Univ. Press, ISBN 0-8014-0134-8

[3] Flory, P.J. (1969) Statistical Mechanics of Chain Molecules, Wiley, ISBN 0-470-26495-0; reissued 1989, ISBN 1-56990-019-1

[4] "Conformations, Solutions, and Molecular Weight" from "Polymer Science & Technology" courtesy of Prentice Hall Professional publications 9 Mart 2008 tarihinde Wayback Machine sitesinde arşivlendi.