Sıralama algoritması
Sıralama algoritması, bilgisayar bilimlerinde ya da matematikte kullanılan, verilen bir listenin elemanlarını belirli bir sıraya sokan algoritmadır. En çok kullanılan sıralama türleri, sayı büyüklüğüne göre sıralama ve alfabetik sıralamadır. Sıralama işleminin verimli yapılması, arama ve birleştirme algoritmaları gibi çalışması için sıralanmış dizilere gereksinim duyan algoritmaların başarımının yüksek olması için önemlidir. Sıralama algoritmaları bilgisayarlarda tutulan verilerin düzenlenmesini ve insan kullanıcı tarafından daha rahat algılanmasını da sağlar.
Sıralama algoritmaları, tanımı çok yalın olmasına karşın çözümü çok karmaşık olan bir işi gerçekleştirdikleri için, üzerinde en fazla araştırma yapılan bilgisayar bilimi konularından biridir. Çoğu kişi sıralama sorununu çözülmüş bir sorun olarak görse de, yeni sıralama algoritmaları üzerinde araştırmalar sürmektedir. Örneğin kütüphane sıralaması ilk olarak 2004 yılında ortaya atılmıştır. Sıralama algoritmaları, sayılarının çok olması ve değişik yaklaşımlar sunmaları nedeniyle özellikle giriş düzeyindeki bilgisayar bilimleri derslerinde büyük O gösterimi ve veri yapıları gibi temel algoritma kavramlarının açıklanması amacıyla yaygın biçimde kullanılırlar.
Sıralama Algoritmaları

Bilgisayar bilimlerinde kullanılan sıralama algoritmaları genellikle aşağıdaki ölçütlere göre sınıflandırılır:
- Hesaplama karmaşıklığı: Dizideki öğelerin karşılaştırılmasının en iyi, ortalama ve en kötü başarımının dizinin boyutu (n) cinsinden gösterilmiş halidir. Olağan uygulamalarda sıralama algoritmalarının iyi durum başarımı O(n log n) ve kötü durum başarımı ise Ω(n²)'dir. Bir sıralama algoritmasının istenen karmaşıklığı O(n)'dir. Yalnızca soyut bir anahtar karşılaştırması yapan bütün sıralama algoritmaları en kötü durumda her zaman Ω(n log n) karşılaştırma yaparlar.
- Yer Değiştirme Karmaşıklığı (yerinde sıralama algoritmaları için).
- Bellek (ve diğer donanım kaynaklarının) Kullanımı: Bazı sıralama algoritmaları dizinin içerdiği öğelerin dizinin saklandığı alanda sıralar. Böylece sıralanan öğeler dışında yalnızca O(1) ya da O(log n)'lik bir ek bellek alanı gerekir. Bazı algoritmalar ise verinin geçici olarak saklanması için dizinin tutulduğu alanın dışında ek bellek alanlarına gereksinim duyar.
- Özyineleme: Bazı algoritmalar ya özyinelemeli ya da özyinelemesiz çalışırken, birleştirmeli sıralama gibi bazı algoritmalar iki biçimde de uygulanabilir
- Kararlılık
- Kaşılaştırma sıralaması olup olmama: Bir karşılaştırma sıralaması sıralanacak veriyi, bir karşılaştırma işlemi kullanarak, karşılaştırarak inceler.
- Genel Yöntem: Araya sokma, değiştirme, seçme, birleştirme vb. Değiştirme sıralamalarına kabarcık sıralaması ve hızlı sıralama örnek olarak gösterilebilir. Yığın sıralaması ise seçme sıralamalarındandır.
Kararlılık
Kararlı sıralama algoritmaları sıralanacak dizinin içinde değerleri birbirine eşit olan öğerlerin birbirlerine göre olan konulmlarını korur. Başka bir deyişle, bir sıralama algoritması kararlı olduğunda, eğer R ve S gibi içerdiği değer aynı olan iki öğe bulunduran asıl dizide, R, S' den önce geliyorsa, sıralanmış dizide de R, S'den önce olur.
Dizinin içinde birbirine eşit değerler içeren öğeler birbirlerinden ayırt edilemiyorsa (örneğin sayılar ya da harfler gibi değerler öğenin kendisini oluşturuyor ise) kararlılık bir sorun değildir. Ancak aşağıda gösterildiği gibi sayı çiftleri, her çiftin virgülden önceki sayısına göre sıralanacağı düşünülürse kararlılık sorunu ortaya çıkar.
(4, 1) (3, 7) (3, 1) (5, 6)
Bu durumda, 2 değişik sonuç mümkündür; ilk çözüm sıralama anahtarlarının değerleri aynı olan öğelerinin sırasını korur, ikincisi ise korumaz:
(3, 7) (3, 1) (4, 1) (5, 6) (sıra korunmuş) (3, 1) (3, 7) (4, 1) (5, 6) (sıra değişmiş)
Kararsız sıralama algoritmaları sıralama anahtarlarının değerleri aynı olan öğelerin dizi içindeki sırasını değiştirebilir ancak kararlı sıralama algoritmaları asla değiştirmez. Kararsız sıralama algoritmaları özellikle kararlı olacak biçimde uygulanabilir. Bunu yapmanın bir yolu yapay olarak anahtar karşılaştırmasını anahtlarının değerleri birbirine eşit olan iki öğenin durumunu belirlemek için asıl listedeki konumlarını ölçüt olarak kullanacak biçimde genişletmektir. Ancak asıl dizideki öğre sırasının hatırlanması çoğu zaman ek saklama alanı gerektirir.
Sıralama Algoritmalarının Listesi
Aşağıdaki tablolarda n dizideki sıralanacak olan eleman sayısını gösterir. "Ortalama" ve "En Kötü" kolonları ilgili durumlardaki karmaşıklığı, "Bellek" kolonu ise listenin sıralanabilmesi için listenin bellekte kapladığı alandan ne kadar daha fazla saklama alanı gerektiğini gösterir.
Karşılaştırma ile Sıralayan Sıralama Algoritmaları
| Adı | Ortalama | En Kötü | Bellek | Kararlı mı? | Yöntem | Diğer Açıklamalar | |
|---|---|---|---|---|---|---|---|
| Kabarcık Sıralaması | — | O(n²) | O(1) | Evet | Değiştirme | ||
| Kokteyl Sıralaması | — | O(n²) | O(1) | Evet | Değiştirme | ||
| Tarak Sıralaması | O(n log n) | O(n log n) | O(1) | Hayır | Değiştirme | Küçük boyutta kodla uygulanabilir | |
| Cüce Sıralaması | — | O(n²) | O(1) | Evet | Değiştirme | ||
| Seçmeli Sıralama | O(n²) | O(n²) | O(1) | Hayır | Seçme | Kararlı bir sıralama olarak uygulanabilir | |
| Eklemeli Sıralama | O(n + d) | O(n²) | O(1) | Evet | Ekleme | d ters çevirme sayısıdır ve O(n²)'dir | |
| Shell Sıralaması | — | O(n log² n) | O(1) | Hayır | Ekleme | ||
| Ağaç Sıralaması | O(n log n) | O(n log n) | O(n) | Evet | Ekleme | Kendini dengeleyen bir ikili arama ağacında kullanıldığında | |
| Kütüphane Sıralaması | O(n log n) | O(n²) | O(n) | Evet | Ekleme | ||
| Birleştirmeli Sıralama | O(n log n) | O(n log n) | O(n) | Evet | Birleştirme | ||
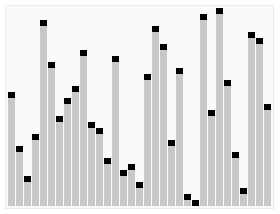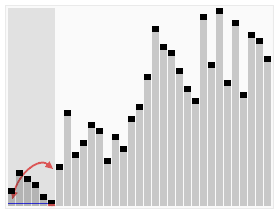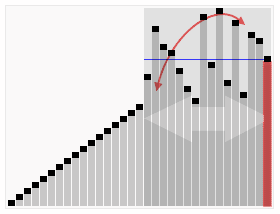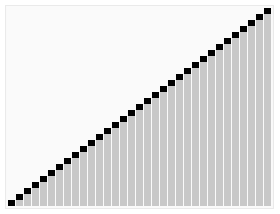
| Yerinde Birleştirmeli Sıralama | O(n log n) | O(n log n) | O(1) | Evet | Birleştirme | Örnek uygulamasını gösteren sayfa: | |
| Yığın Sıralaması | O(n log n) | O(n log n) | O(1) | Hayır | Seçme | ||
| Rahat Sıralama | — | O(n log n) | O(1) | Hayır | Seçme | ||
| Hızlı Sıralama | O(n log n) | O(n²) | O(log n) | Hayır | Bölümlendirme | Yalın uygulamaları O(n) kadar bir alan kullanır; ortada bir pivot kullanılırsa en kötü durumda O(n log n) olabilir | |
| İçgözlemle Sıralama | O(n log n) | O(n log n) | O(log n) | Hayır | Melez | Standart Şablon Kütüphanelerinin çoğunda kullanılır | |
| Sabır Sıralaması | — | O(n²) | O(n) | Hayır | Ekleme | O(n log n) zamanda bütün en uzun artan altdizileri bulur | |
| İplik Sıralaması | O(n log n) | O(n²) | O(n) | Evet | Seçme |


Karşılaştırmadan Sıralayan Sıralama Algoritmaları
Aşağıdaki tablo karşılaştırma kullanmadan sıralama yapan sıralama algoritmalarını göstermektedir. Bu algoritmalar karşılaştırma yapmadıkları için karmaşıklıklarınınO(n log n) gibi bir alt sınırı yoktur. Tabloda gösterilen karmaşıklıklar sıralanacak listedeki eleman sayısı (n), her bir anahtarın boyutu (k) ve uygulama tarafından kullanılan parça boyutu (k) cinsiden yazılmıştır. Algoritmaların pek çoğu anahtar boyutunun bütün satırlarda özgün anahtar değerleri olmasını sağlayacak kadar büyük ve n << 2k ('<<' = "çok daha küçük") olduğunu varsayar.
| Adı | Ortalama | En Kötü | Bellek | Kararlı mı? | n << 2k ? | Diğer Açıklamalar |
|---|---|---|---|---|---|---|
| Güvercin Yuvası Sıralaması | O(n+2k) | O(n+2k) | O(2k) | Evet | Evet | |
| Kova Sıralaması | O(n•k) | O(n²•k) | O(n•k) | Evet | Hayır | Elemanların dizide düzenli olarak dağıldığını varsayar. |
| Sayarak Sıralama | O(n+2k) | O(n+2k) | O(n+2k) | Evet | Evet | |
| En anlamsız Basamağa göre sıralama | O(n•k/s) | O(n•k/s) | O(n) | Evet | Hayır | |
| En anlamlı Basamağa göre sıralama | O(n•k/s) | O(n•(k/s)•2s) | O((k/s)•2s) | Hayır | Hayır | |
| Spreadsort | O(n•k/log(n)) | O(n•(k - log(n)).5) | O(n) | Hayır | Hayır | Asimtotlar n << 2k varsayımına dayanır, ancak algoritmanın buna gereksinimi yoktur. |
Verimsiz Sıralama Algoritmaları
Aşağıdaki tablo çok verimsiz oldukları ya da özel bir donanım gerektirdikleri için gerçek hayatta kullanılması olumlu sonuçlar vermeyecek sıralama algoritmalarını göstermektedir.
| Adı | Ortalama | En Kötü | Bellek | Kararlı mı? | Karşılaştırma sıralaması mı? | Diğer Açıklamalar |
|---|---|---|---|---|---|---|
| Saçma sıralama | O(n × n!) | ∞ | O(1) | Hayır | Evet | Knuth karıştırması kullanılarak ortalama zamanı |
| Rastgele değiştirmeli sıralama | O(n × n!) | ∞ | O(1) | Hayır | Evet | Ortalama zamanı sonuşmayan biçimde saçma sıralamanın yarısıdır |
| Stooge sort | O(n2.71) | O(n2.71) | O(log n) | Hayır | Evet | |
| Bead sort | N/A | N/A | — | N/A | Hayır | Özel donanım gerektirir |
| Simple pancake sort | O(n) | O(n) | O(log n) | Hayır | Evet | Sayı, yapılan değişiklik sayısıdır |
| Sorting networks | O(log n) | O(log n) | O(n•log n) | Evet | Hayır | O(n•log n) boyutunda özel bir devre gerektirir |
Ayrıca bakınız
Dış bağlantılar
- Ardışık ve koşut sıralama algoritmaları13 Aralık 2012 tarihinde Wayback Machine sitesinde arşivlendi.
- Ricardo Baeza-Yates'in sıralama algoritmaları sayfası14 Mart 2008 tarihinde Wayback Machine sitesinde arşivlendi.
- 'Algoritmalar sözlüğü, veri yapıları ve sorular'24 Haziran 2005 tarihinde Wayback Machine sitesinde arşivlendi.
- Slightly Skeptical View on Sorting Algorithms22 Ekim 2012 tarihinde Wayback Machine sitesinde arşivlendi.
- Sorting Revisited15 Nisan 2008 tarihinde Wayback Machine sitesinde arşivlendi.
- QiSort - 2007 yılında ortaya atılmış karmaşıklığı O(n log n) yeni bir sıralama algoritması