Çokludoğrusal altuzay öğrenimi

(MSL) Çokludoğrusal altuzay öğrenme özel bir yapıya sahip çok boyutlu nesnelerin geniş bir alanda belirli bir küçük bir kısmını öğrenmeği hedefliyor.Vektörizasyon işlemine geçmeden,gönderme üzerinden yüksek-boyutlu tensör verilerinin belirli tercih özellikleri olan düşük-boyutlu gösterimini bulmak için bir boyut indirgeme yaklaşımıdır. [1][2] MSL terimi tensör için çok boyutlu diziler anlamına gelir. Tensör veri örnekleri (2D/3D) görüntü'ler içerir.(3D/4D) video dizileri ve hiperspektral küpler (3D/4D).Bir yüksek boyutlu tensör uzayından bir düşük-boyutlu tensör uzayına bir gönderme veya vektör uzayı çoklu doğrusal izdüşümü olarak adlandırılır.[1][3] MSL yöntemleri doğrusal alt uzayı öğrenme metodu olarak temel bileşen analizi (PCA), doğrusal diskriminant analizi (LDA) ve kanonik korelasyon analizi (CCA)'lerinin yüksek mertebeden genellemeleridir.Literatürde, MSL ayrıca tensör alt uzayı öğrenme ve tensör alt uzay analizi olarak adlandırılır.[2] MSL Araştırmaları 2000'lerdeki sezgisel araştırma'sından (on yıl) 2010'ların sistematik incelemesine kadar ilerlemiştir.

Bu sayfa hızlı silinmeye adaydır!

Bu sayfa, Vikipedi'nin hızlı silme politikası gereğince silinmesi için etiketlenmiştir ve bir hizmetli tarafından incelemeyi beklemektedir.
Sayfanın silinmemesi gerektiğini düşünüyorsanız, gerekçenizi tartışma sayfasında belirtiniz ya da silinmeyi gerektiren durumu ortadan kaldıracak şekilde sayfayı düzenleyiniz.
Sağdaki "Göster" düğmesine tıklayarak hızlı silme koşullarına göz atabilirsiniz

(Lütfen bu metni sadece gerekli kuralları hatırlamak için kullanın, VP:HS sayfasındaki kuralları bildiğinizden emin olun. İlgili kriterin aşağıdaki kısaltmalar dışında ek şartları olabilir.)

G1: Anlamsız karakter dizisi — G2: Deneme — G3: Vandalizm — G4: Önceden silinmiş metin — G6: Kullanıcı talebi — G7: Silinmiş sayfanın tartışması — G8: Temizlik amacıyla — G9: Telif — G10: Saldırı — G11: Reklam — G12: İlgisiz tartışma

M1: Taslak kriterlerini sağlamayan madde — M2: Farklı bir dildeki madde — M3: İçeriksiz madde — M4: Başka bir Wikimedia projesine aktarılan madde — M6: Kayda değer olmayan konulu madde — M8: Düzen ve ansiklopediklik açısından uygunsuz madde — M9: Makine çevirisiyle oluşturulmuş madde

Y1: Boşa yönlendirme — Y2: Kötü yönlendirme — Y3: Farklı isim alanları arasında yönlendirme

D1: Çift kopya dosya — D2: Bozuk/boş dosya — D3: Uygunsuz lisanslı dosya — D6: Adil kullanımı hatalı belirtilmiş dosya — D8: Ansiklopedik açıdan değersiz dosya - D9: Kullanışsız dosya - D10: Vektörel dosya - D11: Şüpheli dosya - D12: Tanımlanamayan dosya - D13: İçeriği kaynaklandırılamayan dosya

K1: Boş kategori — K2: Yeniden isimlendirme kategorisi — K3: Şablon kategorisi

KS2: Var olmayan kullanıcı — KS3: Adil kullanım galerisi — KS4: İlgisiz kullanıcı sayfası

Ş1: Kışkırtıcı/bölücü şablon — Ş2: Kullanılmayan şablon

P1: Madde olarak silinebilecek portal — P2: Kriterleri sağlamayan portal

Hizmetliler için: Lütfen sayfanın geçmişini incelemeden silme işlemini gerçekleştirmeyiniz.

Gerekçe: Niteliksiz makine çevirisiyle oluşturulmuş madde
İsteyen: Bu sayfa üzerindeki en son değişiklik, 2 saniye önce Sayginer (katkılar | kayıtlar) tarafından gerçekleştirildi.
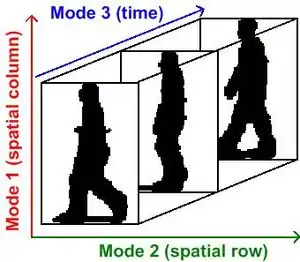
Bir video veya çokludoğrusal altuzay öğrenimi için sütun x satır x zaman çarpımının bir imaj dizi olarak bir üç-sıralı gösterimi

Altyapı

Veri toplama ve depolama teknolojisi'ndeki gelişmeler sayesinde , büyük veri (ya da büyük veri setleri) ortaya çıkan geniş bir yelpazede gelişmekte olan uygulama aralığı içinde bir günlük olarak oluşturulan verilerin çoğu çok boyutludur.Ayrıca,fazlalığın büyük bir miktarı olması nedeniyle çok yüksek boyutlu'lar kullanılır ve sadece giriş uzayının bir kısmını işgal eder.Bu nedenle, boyut indirgeme sık sık mümkün olduğunca çok bilgi koruyarak düşük boyutlu uzayda yüksek boyutlu verileri eşleştirmek için kullanılır.Doğrusal alt uzayı öğrenme,algoritma vektörleri ve bir düşük boyutlu uzaya bir optimal doğrusal gönderme için çözüm olarak veri girişlerinin gösteriminin geleneksel boyut indirgeme teknikleridir.Büyük boyutlu veri ile uğraşırken yazık ki, çoğu zaman yetersiz kalınır. Çok yüksek boyutlu vektörler ile sonuçlanabilir, parametrelerin çok sayıda tahminine ve aynı zamanda orijinal veri,doğal yapısını ve korelasyonu kırmaya yol açar.[1][2][4][5]

Makine öğrenmesi ve
veri madenciliği

MSL tensör bozunması ile yakından ilgilidir .[6] Her ikisi de çoklu doğrusal cebir araçları kullanabilirler. MSL boyut indirgeme'ye odaklanırken fark ise tensör bozunması faktör analizinde odaklanır.MSL tensör-tabanlı hesaplamaya aittir [7] ve makinenin öğrenmesi tensör düzey hesaplamalı düşünce olarak görülebilir.Veri toplama ve depolama teknolojisindeki gelişmeler sayesinde, büyük veri (ya da büyük veri setleri) gelişmekte olan uygulamaları geniş bir yelpazede günlük olarak üretebiliyor. Bu büyük verilerin çoğu çok boyutludur. Ayrıca, artıklığın çok fazla olması nedeniyle, genellikle çok yüksek boyutludur ve sadece giriş uzayının bir kısmını işgal ediyor. Bu nedenle, boyut indirgeme ile sık sık mümkün olduğunca fazla bilgi korunurken düşük boyutlu uzaydaki yüksek boyutlu verileri eşlemek için kullanılır.

Çokludoğrusal izdüşüm
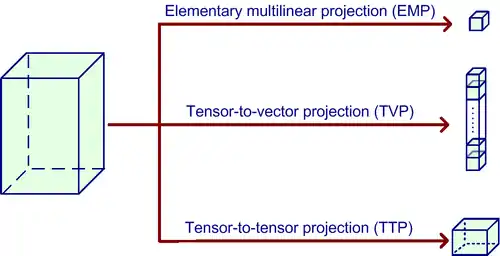
çoklu doğrusal alt uzayı öğrenmek için düşük boyutlu gösterimi bir tensöre dönüştürmeye Çokludoğrusal izdüşüm:Temel çoklu doğrusal izdüşüm (EMP), tensöre-vektör izdüşüm (TVP), ve tensörden-tensöre izdüşüm (TTP)

Bir çoklu doğrusal alt uzay haritası giriş tensör verilerinin bir uzaydan diğerine (düşük-boyutlu) uzay için bir çoklu doğrusal projeksiyonu yoluyla tanımlanır.Hitchcock nedeniyle Orijinal fikir 1927 yılında.[8]

Tensöre-tensör izdüşümü (TTP)

Bir TTP bir N inci-sıralı tensör N izdüşümü matrisleri kullanılarak, aynı sırayla düşük boyutlu tensör için yüksek boyutlu tensörün doğrudan bir yansımasıdır. Her adım, tensör matris çarpımı (ürün) performans ile N adımda gerçekleştirilebilir.N adımlar ile değiştirilemez.[9] Bu izdüşümü üst düzey tekil değer ayrıştırması'nın bir uzantısıdır.[9] (HOSVD) alt uzayı öğrenme.[4] Bundan dolayı, Tucker bozunması'ndan kaynaklandığını görürsünüz [10] in 1960s.

Tensöre-vektör izdüşümü(TVP)

Bir TVP da sıra-bir projeksiyonlar olarak adlandırılır düşük boyutlu bir vektör, bir yüksek boyutlu tensörünün doğrudan bir projeksiyonudur, Ayrıca bu, sıra-bir olarak adlandırılır .TVP bir vektöre bir tensör izdüşümü olarak, bir skalere bir tensör birden çok izdüşüm olarak görülebilir. Böylece,P-boyutlu vektöre bir tensörün TVP(izdüşüm) bir skalere tensör den P izdüşüm oluşur. Bir skalere bir tensör den izdüşümü bir temel çoklu doğrusal izdüşümü (EMP) dür. EMP'de, bir tensör N birimi izdüşümü vektörler aracılığıyla bir noktaya yansıtılır. Her modda tek bir izdüşümü vektörü, (bir skalar sonuçlanan) tek bir hat üzerinde bir tensörün projeksiyonudur. Bu nedenle, "P-boyutlu vektör uzayında bir vektöre bir tensör nesnesinin TVP'u olur P EMP'lerin oluşur. Bu kurallı bozunma'nın izdüşümsel bir uzantısıdır,[11] Ayrıca, paralel faktör'ler (PARAFAC) olarak bilinen bozunmadır[12]

MSL içinde Tipik yaklaşım

Çözülmesi gereken parametrelerin her mod içinde bir N seti vardır.. Bir dizi çözümü, genellikle (olduğunda N=1 olması dışında, doğrusal durum) sıklıkla diğer setlere bağlıdır.Bu nedenle'de suboptimal yinelemeli bir prosedür takip edilmektedir [13] is followed.

  1. Her modda projeksiyonların başlatılması
  2. Her mod için, tüm diğer modunda izdüşümü sabitleme ve mevcut modunda projeksiyon çözer.
  3. Birkaç tekrarlamadan veya yakınsama kadar akıllı-mod optimizasyonu olur.

Bu çok yönlü veri analizi için alternatif en küçük kareler yönteminden kaynaklanmaktadır.[14]

Olumlu ve olumsuz yönleri
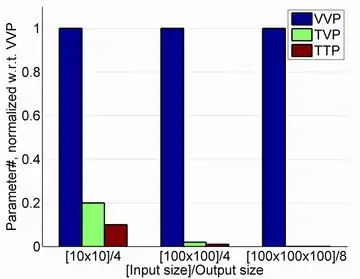
Bu şekil vektör-vektör izdüşümü (VVP) tarafından boyut indirgeme aynı miktarda tahmin edilecek parametre sayısını karşılaştırır, (yani, doğrusal izdüşümü,) tensör-vektör izdüşümü (TVP), ve tensör-to-tensör izdüşümü (TTP).Çokludoğrusal projeksiyonlar çok daha az parametreleri gerektirir ve elde edilen gösterimleri daha kompakt yapıdadır. (Bu şekil araştırma kağıdı Tablo 3'e dayalı üretilir[1])

MSL'nin avantajları:[1][2][4][5]

  • Bu çokluboyutlu verilerin doğal tensörel gösterimi işlemi tarafından orijinal verideki önceki izdüşüm yapısını ve korelasyonu korunur.
  • Onun doğrusal muadili daha kompakt sunumlarını öğrenebilirsiniz. Bu parametrelerin çok daha küçük bir sayısını tahmin etmek gerekiyor ve küçük örneklem boyutu senaryoda daha az sorunları yaratır.
  • Bu doğrusal yöntemlere göre çok daha düşük boyutta hesaplamaları ile daha verimli büyük tensör verilerini halledebiliriz. Böylece, hesaplamalı kaynaklara daha düşük talebe yol açar.

MSL'nin dezavantajları:[1][2][4][5]

  • En MSL algoritması yinelemeli bulunmaktadır. Onlar ilklendirme yöntemi ile etkilenebilir ve yakınsama sorunu olabilir.
  • Elde edilen yerel en iyi çözümdür.

Algoritmalar
  • PCA'nın çokludoğrusal uzantısı
    • TTP-tabanlı: Çokludoğrusal Temel Bileşen Analizi (MPCA) [4]
    • TVP-tabanlı: İlintisiz çokludoğrusal Temel Bileşen Analizi(UMPCA) [15]
  • LDA'nın çokludoğrusal uzantısı
    • TTP-tabanlı:Diskriminant analizi ile tensör gösterimi(DATER) [5]
    • TTP-tabanlı: Genel tensör diskriminant analizi (GTDA) [16]
    • TVP-tabanlı: İlintisiz çokludoğrusal Diskriminant Analizi (UMLDA) [17]
  • CCA çoklu doğrusal uzantısı
    • TTP-tabanlı: Tensor kurallı korelasyon Analizi (TCCA) [18]

Eğitsel kaynakları

Kodlar

Tensor veri kümeleri

Ayrıca bakınız

Kaynakça
  1. Lu, Haiping; Plataniotis, K.N.; Venetsanopoulos, A.N. (2011). "A Survey of Multilinear Subspace Learning for Tensor Data" (PDF). Pattern Recognition. 44 (7). ss. 1540-1551. doi:10.1016/j.patcog.2011.01.004. 10 Temmuz 2019 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 21 Kasım 2013.
  2. X. He, D. Cai, P. Niyogi, Tensor subspace analysis 19 Temmuz 2011 tarihinde Wayback Machine sitesinde arşivlendi., in: Advances in Neural Information Processing Systemsc 18 (NIPS), 2005.
  3. Vasilescu, M.A.O.; Terzopoulos, D. (2007). Multilinear Projection for Appearance-Based Recognition in the Tensor Framework. IEEE 11th International Conference on Computer Visioncc. ss. 1-8. doi:10.1109/ICCV.2007.4409067.
  4. H. Lu, K. N. Plataniotis, and A. N. Venetsanopoulos, "MPCA: Multilinear principal component analysis of tensor objects," IEEE Trans. Neural Netw., vol. 19, no. 1, pp. 18–39, January 2008.
  5. S. Yan, D. Xu, Q. Yang, L. Zhang, X. Tang, and H.-J. Zhang, "Discriminant analysis with tensor representation," in Proc. IEEE Conference on Computer Vision and Pattern Recognition, vol. I, June 2005, pp. 526–532.
  6. T. G. Kolda, B. W. Bader, Tensor decompositions and applications, SIAM Review 51 (3) (2009) 455–500.
  7. "Future Directions in Tensor-Based Computation and Modeling" (PDF). Mayıs 2009. 11 Ocak 2016 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 21 Kasım 2013.
  8. F. L. Hitchcock (1927). "The expression of a tensor or a polyadic as a sum of products". Journal of Mathematics and Physics. Cilt 6. ss. 164-189.
  9. L.D. Lathauwer, B.D. Moor, J. Vandewalle, A multilinear singular value decomposition, SIAM Journal of Matrix Analysis and Applications vol. 21, no. 4, pp. 1253–1278, 2000
  10. Ledyard R Tucker (Eylül 1966). "Some mathematical notes on three-mode factor analysis". Psychometrika. 31 (3). ss. 279-311. doi:10.1007/BF02289464.
  11. J. D. Carroll & J. Chang (1970). "Analysis of individual differences in multidimensional scaling via an n-way generalization of 'Eckart–Young' decomposition". Psychometrika. Cilt 35. ss. 283-319. doi:10.1007/BF02310791.
  12. R. A. Harshman, Foundations of the PARAFAC procedure: Models and conditions for an "explanatory" multi-modal factor analysis 10 Ekim 2004 tarihinde Wayback Machine sitesinde arşivlendi.. UCLA Working Papers in Phonetics, 16, pp. 1-84, 1970.
  13. L. D. Lathauwer, B. D. Moor, J. Vandewalle, On the best rank-1 and rank-(R1, R2, ..., RN ) approximation of higher-order tensors, SIAM Journal of Matrix Analysis and Applications 21 (4) (2000) 1324–1342.
  14. P. M. Kroonenberg and J. de Leeuw, Principal component analysis of three-mode data by means of alternating least squares algorithms, Psychometrika, 45 (1980), pp. 69–97.
  15. H. Lu, K. N. Plataniotis, and A. N. Venetsanopoulos, "Uncorrelated multilinear principal component analysis for unsupervised multilinear subspace learning," IEEE Trans. Neural Netw., vol. 20, no. 11, pp. 1820–1836, November 2009.
  16. D. Tao, X. Li, X. Wu, and S. J. Maybank, "General tensor discriminant analysis and gabor features for gait recognition," IEEE Trans. Pattern Anal. Mach. Intell., vol. 29, no. 10, pp. 1700–1715, October 2007.
  17. H. Lu, K. N. Plataniotis, and A. N. Venetsanopoulos, "Uncorrelated multilinear discriminant analysis with regularization and aggregation for tensor object recognition," IEEE Trans. Neural Netw., vol. 20, no. 1, pp. 103–123, January 2009.
  18. T.-K. Kim and R. Cipolla. "Canonical correlation analysis of video volume tensors for action categorization and detection," IEEE Trans. Pattern Anal. Mach. Intell., vol. 31, no. 8, pp. 1415–1428, 2009.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.