Öteleme

Öklid geometrisinde bir öteleme, belli bir yönde sabit bir uzaklık kadar yer değiştirme demektir. Eşölçer dönüşümlerden biridir (diğerleri dönme ve yansımadır). Ötelemenin bir diğer yorumu, her noktaya sabit bir vektör eklemek, veya koordinat sistemini kaydırmaktır. Bir öteleme operatörü ${\displaystyle T_{\mathbf {\delta } }}$ şöyle tanımlanır: ${\displaystyle T_{\mathbf {\delta } }f(\mathbf {v} )=f(\mathbf {v} +\mathbf {\delta } ).}$

Öteleme bir şekli oluşturan her noktayı belli bir yönde aynı uzaklık kadar yerini değiştirir.

bir eksene karşı karşı bir yansıması tarafından izlenen bir yansıma bir ikinci eksene paralel olarak ötelemesidir toplam hareket ile sonuçlanır.

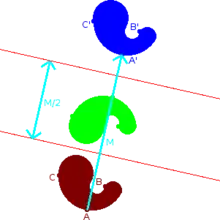
Eğer v sabit vektör ise T_v ötelemesi T_v(p) = p + v olarak çalışır. Eğer T bir öteleme, A altında fonksiyon T nin bir altkümesinin görüntü'sü ise T tarafından Anın ötelemesidir Bu öteleme T_v tarafından sıklıkla A + v olarak yazılır.

Bir Öklid uzayı'nda, herhangi bir öteleme bir izometri'dir.Bu bütün ötelemelerin formlarının kümesi T öteleme grubu,uzayın kendisine izomoriktir, ve Öklidyen grup E(n )'nin bir normal altgrup'udur.E(n )'nin kota grubu T tarafından ortogonal grup O(n )ya izomorfiktir:

E(n ) / T ≅ O(n ).

Matris gösterimi

Bir ötelemede bir benzeşik dönüşüm ile sabit nokta'lar yoktur. Matris çarpımında her zaman orijin olarak bir sabit nokta vardır.yine de, burada bir vektör uzayı ile matris çarpımı'nın bir ötelemesinin gösterimine bir ortak geçici çözüm olarak kullanılan homojen koordinatlar :

3-boyutlu vektör w olarak şu yazılır

w= (w_x, w_y, w_z)

kullanılan 4 homojen koordinat olarak

w = (w_x, w_y, w_z, 1).[1]

Bir vektör v tarafından bir nesnenin ötelemesi, her homojen vektör p (homogen koordinatlar içinde yazılır) bu öteleme matrisi tarafından çarpılabilir:

${\displaystyle T_{\mathbf {v} }={\begin{bmatrix}1&0&0&v_{x}\\0&1&0&v_{y}\\0&0&1&v_{z}\\0&0&0&1\end{bmatrix}}}$

Aşağıda gösterildiği gibi, çarpma beklenen sonucu verecektir:

${\displaystyle T_{\mathbf {v} }\mathbf {p} ={\begin{bmatrix}1&0&0&v_{x}\\0&1&0&v_{y}\\0&0&1&v_{z}\\0&0&0&1\end{bmatrix}}{\begin{bmatrix}p_{x}\\p_{y}\\p_{z}\\1\end{bmatrix}}={\begin{bmatrix}p_{x}+v_{x}\\p_{y}+v_{y}\\p_{z}+v_{z}\\1\end{bmatrix}}=\mathbf {p} +\mathbf {v} }$

Bir çeviri matrisin ters vektör yönünü tersine çevrilmesi elde edilebilir:

${\displaystyle T_{\mathbf {v} }^{-1}=T_{-\mathbf {v} }.\!}$

Benzer şekilde, çeviri matrislerin çarpım vektörleri eklenerek verilir:

${\displaystyle T_{\mathbf {u} }T_{\mathbf {v} }=T_{\mathbf {u} +\mathbf {v} }.\!}$

Çünkü vektörlerin eklemeli değişmelisidir,öteleme matrislerinin çarpımı bu nedenle değişmeli (keyfi matrislerin çarpımının aksine)dir.

Fizikte öteleme

Fizik'te, öteleme (ötelemeli hareket)hareketli bir nesnenin pozisyon değişikliğidir,döndürme'ye karşıttır. örneğin, Whittakere göre:[2]

Bir cisim bir pozisyondan başka bir pozisyona hareket ettirilirse ve cisim noktalarına her ilk ve son noktaları birleştiren hat uzunluğunun paralel düz çizgiler bir ℓ dizisi ise, uzayda cismin yönü değişmeden böylece bir ℓ mesafesi boyunca çizgilerin yönünde paralel olarak öteleme , bir yerdeğiştirme olarak adlandırılır .

— E.T. Whittaker: A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, p. 1

Bir öteleme formülüne göre, bir nesnenin tüm noktalarının konumlarını (x, y, z) değişen bir işlemdir.

${\displaystyle (x,y,z)\to (x+\Delta x,y+\Delta y,z+\Delta z)}$

burada ${\displaystyle (\Delta x,\ \Delta y,\ \Delta z)}$ vektör nesnenin her noktası için aynıdır. Bu öteleme vektörü ${\displaystyle (\Delta x,\ \Delta y,\ \Delta z)}$ tanımlanan nesnenin yerdeğiştirme'sinin özel tipinin bütün noktalarına ortaktır,kullanılan bir doğrusal rotasyon içeren değiştirmelerden onu ayırmak için değiştirme açısal yerdeğiştirmeler olarak adlandırılır.

Uzayın (veya zamanın) bir ötelemesi Bir nesnenin bir ötelemesi ile karıştırılmamalıdır. Bu tür ötelemelerde sabit noktalar yoktur.

Ayrıca bakınız

• Ötelemeli simetri
• Dönüşüm matrisi
• Rotasyon matrisi
• Ölçümleme
• Adveksiyon

Dış bağlantılar

• Translation Transform16 Mayıs 2008 tarihinde Wayback Machine sitesinde arşivlendi. at cut-the-knot
• Geometric Translation (Interactive Animation)18 Aralık 2008 tarihinde Wayback Machine sitesinde arşivlendi. at Math Is Fun
• Understanding 2D Translation15 Aralık 2008 tarihinde Wayback Machine sitesinde arşivlendi. and Understanding 3D Translation17 Eylül 2008 tarihinde Wayback Machine sitesinde arşivlendi. by Roger Germundsson, The Wolfram Demonstrations Project.

Kaynakça

1. Richard Paul, 1981, Robot manipulators: mathematics, programming, and control : the computer control of robot manipulators, MIT Press, Cambridge, MA
2. Edmund Taylor Whittaker (1988). A Treatise on the Analytical Dynamics of Particles and Rigid Bodies (Reprint of fourth edition of 1936 with foreword by William McCrea bas.). Cambridge University Press. s. 1. ISBN 0-521-35883-3.