Ampère yasası

Klasik elektromanyetizmada Ampère yasası (1826'da André-Marie Ampere tarafından bulunmuştur) kapalı bir eğri üzerinden integrali alınmış manyetik alanla o eğri üzerindeki elektrik akımı arasındaki ilişkiyi açıklayan yasadır. James Clerk Maxwell yasayı hidrodinamik olarak 1861 tarihli Fizikte kuvvet çizgileri üzerine makalesinde tekrar kanıtlar. Yasanın matematiksel ifadesi şu anda klasik elektromanyetizmayı oluşturan dört temel Maxwell denkleminden biridir.

Orijinal Ampere yasası

Manyetik alan oluşturan elektrik yükü.

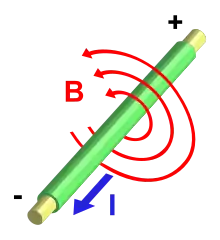
Tarihsel olarak ilk ortaya çıktığı hâliyle Ampere yasası manyetik alanı bu alanı oluşturan elektrik akımıyla ilişkilendirir. Yasa integral denklemi olarak da diferansiyel denklem olarak da yazılabilir. Bu iki form tek bir yasaya tekabül eder ve birbiriyle Kelvin-Stoke teoremi ile bağlantılıdır.

İntegral formu

SI birimleriyle Amper yasasının integral formu aşağıdaki gibidir.

${\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}\iint _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S} }$

${\displaystyle \oint _{C}\mathbf {H} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{S}\mathbf {J} _{\mathrm {f} }\cdot \mathrm {d} \mathbf {S} }$

ya da

${\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}I_{\mathrm {enc} }}$

${\displaystyle \oint _{C}\mathbf {H} \cdot \mathrm {d} {\boldsymbol {\ell }}=I_{\mathrm {f,enc} }}$

${\displaystyle \textstyle \oint _{C}}$ kapalı C eğrisi üzerinden alınan çizgi integrali,

B manyetik alan (birimi Tesla),

· vektörlerin skaler çarpımı,

dℓ eğrinin sonsuz küçüklükteki (diferansiyel) elementi (büyüklüğü C eğrisinin sonsuz küçüklükteki parçasının büyüklüğüne ve doğrultusu o parçaya teğet olan doğru üzerinde olan vektör),

${\displaystyle \textstyle \iint _{S}}$ eğri tarafından kapatılan S alanı üzerinden iki boyutlu integral,

μ₀ manyetik sabit,

J_f eğri tarafından kapatılan S alanından geçen serbest yük yoğunluğu,

J alandan geçen serbest ve bağlı akım yoğunluğu toplamı,

dS sonsuz küçüklükteki alan elementi (S alanının sonsuz küçüklükteki parçasının alanı boyutunda ve bu parçaya dik doğrultuda olan vektör; vektörün yönü C eğrisinin yönelimine göre sağ el kaidesiyle bağlıdır),

I_f,enc eğri ile kapatılan alandan geçen net serbest akım,

I_enc alandan geçen serbest ve bağlı net toplam akım.

Yukarıdaki tanımla ilgili birkaç belirsizlik vardır. Birincisi, üç terimde işaret belirsiziği (pozitif ya da negatif) söz konusudur: çizgi integrali eğri etrafında saat yönünde ya da aksi yönde alınabilir, dS alana dik olan doğrultuda iki yönde de olabilir, I_enc belirlenmiş alandan geçen akımdır ve o alandan bir yönde geçen akım diğer yönde geçen akımın negatif işaretlisi olacağından bu yönlerden birisinin seçilmesi gerekir. Bu belirsizlikler sağ el kaidesiyle ortadan kalkar: Sağ elin avuç içi üzerinden integal alınacak alana bakarken işaret parmağı integralin yönünü gösterdiğinde baş parmağın gösterdiği yön dS vektörünün yönünü verir, bu yönde geçen akımın işareti de pozitif alınır. İkinci olarak, C eğrisinin sınırlarını belirlediği sonsuz sayıda S alanı vardır ve bu alanlardan hangisinin seçileceği bir problemdir. Eğer C bir düzlem üzerinde değilse S'nin seçimi için bariz bir yol yoktur. Bunun cevabı, hangi S'nin seçileceğinin önemli olmamasıdır. Sınırları C olan herhangi bir alanın aynı sonucu vereceği kanıtlanabilir.

Diferansiyel formu

Kelvin-Stoke teoremiyle integral denklemi diferansiyel forma dönüştürülebilir. İntegral formu gibi bu form da sadece elektrik alanının sabit olduğu statik durumlar için geçerlidir. SI birimleriyle Amper yasasın daha genel olan diferansiyel formu aşağıdaki gibidir (:${\displaystyle \mathbf {\nabla } \times \!\ }$ rotasyonel operatör).

${\displaystyle \mathbf {\nabla } \times \mathbf {B} =\mu _{0}\mathbf {J} }$

${\displaystyle \mathbf {\nabla } \times \mathbf {H} =\mathbf {J_{f}} }$

Serbest akım ve bağlı akım üzerine not

Basit seviyelerdeki ders kitaplarında geçen akımlar “serbest akım” olarak sınıflandırılabilir (örneğin bir telden ya da bataryadan geçen akım). Bunun haricinde, manyetize ya da polarize olabilen (her madde bir dereceye kadar olabilir) maddelerden geçen akımlara “bağlı akım” denir.

Bir madde manyetize olduğunda (mesela haricî bir manyetik alan içerisine koyularak) elektronlar kendi atomlarına bağlı kalmakla beraber çekirdek etrafında belirli bir yönde dönerek mikroskopik bir akım yaratıyormuş gibi davranırlar. Madde içerisindeki bütün bu akımlar bir araya geldiğinde akım makroskopik ölçüde etki yaratacak kadar büyür. Bu manyetizasyon akımı J_M bağlı akıma katkıda bulunur.

Bağlı akımın diğer bir kaynağı bağlı yüklerdir. Haricî bir elektrik alan altında, polarize olabilen materyallerin pozitif ve negatif yükleri madde içerisinde ayrışır ve bağlı yüklerin hareketi sonucu ortaya bağlı akımın diğer kaynağı olan polarizasyon akımı J_P çıkar.

Böylece toplam akım yoğunluğunu J serbest akım yoğunluğunu belirtmek üzere aşağıdaki gibi yazabiliriz.

${\displaystyle \mathbf {J} =\mathbf {J_{f}+J_{M}+J_{P}} \ ,}$

Mikroskopik açıdan bütün bu akımlar aynı türdendir fakat bağlı akımları serbest akımdan ayırt etmenin pratik faydaları vardır. Söz gelimi, bağlı akım genellikle atomik boyutlarda ortaya çıktığından, büyük boyutlu materyaller söz konusu olduğunda Amper yasası B ve mikroskopik akımların toplamı (yukarıda bahsedilen üç akım) şeklinde yazılmaktansa H ve yalızca serbest akım kullanarak ifade edilebilir. H ya da B kullanılarak yazılan denklemlerin eşdeğerliği aşağıda kanıtlanacaktır.

Orijinal yasasın genişletilmiş hali: Maxwell-Ampère denklemi

Serbest yükleri bağlı olanlardan ayrı olarak inceleyerek Maxwell'in düzeltmesini de içerecek şekilde ve H-alanı cinsinden yazılan Ampere yazası aşağıdaki gibidir (H-alanı manyetizasyon akımını da içerdiğinden denklemde J_M açık biçimde görülmez).

${\displaystyle \oint _{C}\mathbf {H} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{S}\left(\mathbf {J} _{\mathrm {f} }+{\frac {\partial }{\partial t}}\mathbf {D} \right)\cdot \mathrm {d} \mathbf {A} }$

H manyetik H-alanı (yardımcı manyetik alan, manyetik alan kuvveti ya da sadece manyetik alan diye de anılır), D elektriksel yer değiştirme alanı ve J_f serbest akım yoğunluğu olmak üzere integral formunda olan bu denklem diferansiyel formda şöyle görülür:

${\displaystyle \mathbf {\nabla } \times \mathbf {H} =\mathbf {J} _{\mathrm {f} }+{\frac {\partial }{\partial t}}\mathbf {D} \ .}$

Öte yandan yüklerin serbest ya da bağlı olduğu göz önünde bulundurulmaksızın denklem genelleştirilmiş Ampere yasasında (Maxwell-Ampere yasası da denir) şu şekilde geçer:

${\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{S}\left(\mu _{0}\mathbf {J} +\mu _{0}\epsilon _{0}{\frac {\partial }{\partial t}}\mathbf {E} \right)\cdot \mathrm {d} \mathbf {A} }$

Diferansiyel formda:

${\displaystyle \mathbf {\nabla } \times \mathbf {B} =(\mu _{0}\mathbf {J} +\mu _{0}\epsilon _{0}{\frac {\partial }{\partial t}}\mathbf {E} )\ .}$

İki formda da J manyetizasyon akım yoğunluğunu, polarizasyon akım yoğunluğunu ve serbest akım yoğunluğunu içerecek şekildedir yani denklemin sağ tarafındaki yük yoğunluğu:

${\displaystyle \mathbf {J_{f}+J_{D}+J_{M}} =\mathbf {J_{f}+J_{P}+J_{M}} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}=\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\ ,}$

J_D yer değiştirme akımı, J yüklerin yer değiştirmesinden (serbest ve bağlı) doğan akım yoğunluğu.

∇ · D = ρ olduğundan, Ampere'in orijinal formülasyonunda ortaya çıkan yüklerin sürekliliği problemi ε₀∂E / ∂t teriminin sağladığı üzere boş uzayda dalganın yayılmasının mümkün oluşu sayesinde ortadan kalkar.

Yer değiştirme akımını denkleme ekleyen Maxwell ışığın bir elektromanyetik dalga olduğunu doğru bir biçimde öngördü (bkz. elektromanyetik dalga denklemi).

Eşdeğerlik kanıtı

Ampere yasasınun sadece serbest akımı içeren terimlerle yazıldığı formunun, toplam akımı içeren terimlerle yazılan formuna eşdeğer olduğunun kanıtı aşağıdaki gibi yapılabilir.

Matematiksel olarak, eşdeğerliği gösterilecek denklemler aşağıdaki şekilde yazılabilir (kanıtta sadece diferansiyel formlarla ilgileneceğiz fakat denklemlerin integral formu burada görülecek olan her denkleme Kelvin-Stoke teoremiyle bağlanabilir).

${\displaystyle \nabla \times \mathbf {H} =\mathbf {J} _{f}+{\frac {\partial \mathbf {D} }{\partial t}}}$

${\displaystyle \mathbf {\nabla } \times \mathbf {B} /\mu _{0}=\mathbf {J} +\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}}$

Polarizasyon yoğunluğu P'yi ve manyetizasyon yoğunluğu M'yi aşağıdaki gibi tanımlayalım.

${\displaystyle \mathbf {D} =\epsilon _{0}\mathbf {E} +\mathbf {P} }$

${\displaystyle \mathbf {B} /\mu _{0}=\mathbf {H} +\mathbf {M} }$

Böylece, aşağıdaki iki değeri manyetizasyon akımı yoğunluğu ve polarizasyon akımı yoğunluğu şeklinde adlandırabiliriz.

${\displaystyle \mathbf {J} _{\mathrm {M} }=\nabla \times \mathbf {M} \ ,}$

${\displaystyle \mathbf {J} _{\mathrm {P} }={\frac {\partial \mathbf {P} }{\partial t}}\ ,}$

Toplam bağlı akım yoğunluğunu bu iki değer ile ifade edersek,

${\displaystyle \mathbf {J} _{\mathrm {bound} }=\nabla \times \mathbf {M} +{\frac {\partial \mathbf {P} }{\partial t}}\ ,}$

${\displaystyle =\mathbf {J} _{\mathrm {M} }+\mathbf {J} _{\mathrm {P} }\ ,}$

B için geçerli olan denklemi alalım,

${\displaystyle \mathbf {\nabla } \times \mathbf {B} /\mu _{0}=\mathbf {\nabla } \times \left(\mathbf {H+M} \right)}$

${\displaystyle =\mathbf {\nabla } \times \mathbf {H} +\mathbf {J_{M}} }$

${\displaystyle =\mathbf {J_{f}} +\mathbf {J_{P}} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}+\mathbf {J_{M}} }$

Sonuç olarak, bağlı akımın tanımını göz önünde bulundurarak,

${\displaystyle \mathbf {\nabla } \times \mathbf {B} /\mu _{0}=\mathbf {J_{f}} +\mathbf {J} _{\mathrm {bound} }+\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}}$

${\displaystyle =\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\ ,}$

Gauss birimlerinde Ampère yasası

Gauss birimlerinde yasanın integral formu (Maxwell'in düzeltmesiyle birlikte) c ışık hızı olmak üzere şu hâli alır:

${\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}={\frac {1}{c}}\iint _{S}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}\right)\cdot \mathrm {d} \mathbf {S} }$

Denklemin diferansiyel formda ifadesi aşağıdaki gibidir.

${\displaystyle \mathbf {\nabla } \times \mathbf {B} ={\frac {1}{c}}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}\right).}$

İlgili makaleler

• Biot–Savart yasası
• Yer değiştirme akımı
• Kapasitans
• Elektromanyetik dalga denklemi
• Faraday endüksiyon yasası
• Bağlı yük
• Elektrik akımı
• Vektör kalkulus
• Stokes teoremi

Dış bağlantılar

• https://www.youtube.com/watch?v=ai_xT8Lj2lk Ampere Yasası (Türkçe)
• Simple Nature by Benjamin Crowell3 Haziran 2011 tarihinde Wayback Machine sitesinde arşivlendi. Online bir kitaptan Amper yasası (İngilizce)
• MISN-0-138 Ampere's Law (PDF dosyası) Kirby Morgan tarafından Project PHYSNET14 Mayıs 2017 tarihinde Wayback Machine sitesinde arşivlendi. kapsamında yazıldı (İngilizce).
• MISN-0-145 The Ampere–Maxwell Equation; Displacement Current22 Ekim 2005 tarihinde Wayback Machine sitesinde arşivlendi. (PDF dosyası) J.S. Kovacs tarafından Project PHYSNET kapsamında yazıldı (İngilizce).
• The Ampère's Law Song11 Ekim 2010 tarihinde Wayback Machine sitesinde arşivlendi. (PDF dosyası) Walter Fox Smith tarafından yazıldı (İngilizce).
• A Dynamical Theory of the Electromagnetic Field28 Temmuz 2011 tarihinde Wayback Machine sitesinde arşivlendi. Maxwell'in 1864 tarihli makalesi (İngilizce)