Eşbölüşüm teoremi

Klasik istatistik fizikte eşbölüşüm teoremi bir sistemin ortalama enerjisi ile sıcaklığı arasında ilişki kuran genel bir teoremdir. Eşbölüşüm teoremi ayrıca eşbölüşüm yasası, enerjinin eşbölüşümü veya basitçe eşbölüşüm olarak da bilinir. Eşbölüşümün temel düşüncesi, termal dengede enerjinin çeşitli formları arasında eşit olarak paylaşılmasıdır; örneğin bir molekülün öteleme hareketindeki ortalama kinetik enerjisi dönme hareketindeki ortalama kinetik enerjiye eşit olmalıdır.

Alfa helikal peptitin termal hareketi. Hareket rastgele ve karmaşık ve her bir atomun enerjisi hızlıca değişebiliyor. Bununla birlikte eşbölüşüm teoremi her atomun ortalama kinetik enerjisinin ve çoğu titreşim kiplerinin ortalama potansiyel enerjisinin hesaplanabilmesini sağlıyor. Şekildeki gri, kırmızı ve mavi küreler karbon, oksijen ve azot atomlarını daha küçük beyaz küreler de hidrojen atomunu temsil ediyor.

Eşbölüşüm teoremi kantitatif tahminler yapar. Virial teoremi gibi, bir sistem için, verilen sıcaklıkta, toplam ortalama kinetik ve potansiyel enerjiyi verir bunlarla sistemin ısı kapasitesi hesaplanabilir. Eşbölüşüm, bir parçacığın kinetik enerjisi veya bir yayın potansiyel enerjisi gibi, enerjinin bireysel bileşenlerinin de ortalama değerini verir. Örneğin, eşbölüşüm termal dengedeki bir ideal gazın her molekülünün (3/2)kBT'lik bir kinetik enerjiye sahip olduğunu öne sürer, burada kB Boltzmann sabitidir ve T sıcaklıktır. Genel olarak ne kadar karışık olduğuna bakılmaksızın termal dengedeki herhangi bir klasik sisteme uygulanabilir. Eşbölüşüm teoremi katıların spesifik ısı kapasiteleri için klasik ideal gaz yasasının ve Dulong–Petit yasasının türetiminde kullanılabilir. Teorem ayrıca, rölativistik etkiler göz önünde tutulduğunda dahi, yıldızların (nötron yıldızları ve cüce yıldızlar da dahil) özellikleri ile ilgili öngörülerde kullanılabilir.

Eşbölüşüm teoremi belirli koşullarda hatasız tahminler yapabilmesine rağmen, özellikle düşük sıcaklıklarda kuantum etkisinin belirgin olduğu durumlarda hatalı olur. Termal enerji (3/2)k_BT belirli serbestlik derecelerinde kuantum enerji aralığından düşük olduğunda, ortalama enerji ve serbestlik derecesinin ısı kapasitesi eşbölüşümün öngördüğünden daha düşük olur.

Tarihi

Kinetik enerjinin eşbölüşümü ilk olarak 1843'te ve daha doğru bir şekilde 1845'te John James Waterston tarafından ileri sürüldü.[1] 1859'da James Clerk Maxwell bir gazın kinetik ısı enerjisinin çizgisel ve dönme enerjisine eişt olarak bölündüğünü öne sürdü.[2] 1876'da Ludwig Boltzmann bu prensibi, bir sistemdeki ortalama enerjinin hareketin bütün bağımsız bileşenlerine eşit olarak bölüneceğini göstererek genişletti.[3][4] Boltzman katıların özgül ısı kapasiteleri için Dulong–Petit yasasının kuramsal açıklamasını sağlamak için eşbölüşüm teoremini kullandı.

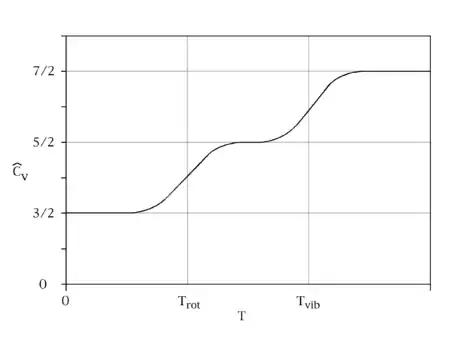
Eşbölüşüm teoreminin tarihi özgül ısı kapasitesininki ile iç içe geçmiştir. Her ikisi de 19. yüzyılda araştırıldı. 1819'da Fransız fizikçiler Pierre Louis Dulong ve Alexis Thérèse Petit oda sıcaklığında katı elementlerin özgül ısı kapasitelerinin elementin atom ağırlığı ile ters orantılı olduğunun keşfettiler.[5] Onların yasası yıllarca atom ağırlığının hesaplanması için bir teknik olarak kullanıldı.[6] Ancak James Dewar ve Heinrich Friedrich Weber'in takip eden araştırmaları Dulong–Petit yasasının sadece yüksek sıcaklıklarda geçerli olduğunu gösterdi;[7] düşük sıcaklıklarda ve elmas gibi son derece sert katılarda özgül ısı kapasitesi daha düşüktü.[8]

Gazlar için özgül ısı kapasitesi üzerine yapılan deneysel gözlemler de eşbölüşüm teoreminin geçerliliği hakkındaki endişeleri artırdı. Teorem molar ısı kapasitesinin basit tek atomlu gazlar için kabaca 3 cal/(mol·K) iken iki atomlu gazlar için 7 cal/(mol·K) olması gerktiğini öngörür. Deneyler eski tahmini doğruladı[9] fakat iki atomlu gazlar için molar ısı kapasiteleri sıklıkla yaklaşık 5 cal/(mol·K) olarak bulundu,[10] ve düşük sıcaklıklarda yaklaşık olarak 3 cal/(mol·K) değerine düşüyordu.[11] Maxwell 1875'te deney ve eşbölüşüm arasındaki uyuşmazlığın bu sayıların gösterdiğinden daha kötü olduğuna işaret etti;[12] atomların iç kısımları var olduğu için ısı enerjisi bu iç kısımların hareketine gitmesi gerekir, bu da tek atomlu ve iki atomlu gazlar için öngörülen özgül ısı kapasitelerinin 3 cal/(mol·K) ve 7 cal/(mol·K) değerinden daha büyük yapar.

Üçüncü bir çelişki metallerin özgül ısısıyla ilgilidir.[13] Klasik Drude modeline göre metal elektronları neredeyse ideal gaz gibi davranır, yani elektronlar ısı kapasitesine (3/2) N_ek_B kadar katkıda bulunmalıdır. Buradaki N_e elektron sayısını verir. Ancak deneysel olarak elektronların ısı kapasitesine katkıları küçüktür: çoğu iletkenin ve yalıtkanın molar ısı kapasiteleri neredeyse aynıdır.[13]

Eşbölüşümün molar ısı kapasitesini açıklamaktaki başarısızlığı konusunda muhtelif açıklamalar getirildi. Boltzmann eşbölüşüm kuralının türetilişinin doğruluğunu savundu, ancak gazların esirle olan etkileşimlerinden dolayı termal dengede olamayabileceğini söyledi.[14] Lord Kelvin eşbölüşüm teoreminin deneylerle uyuşmadığı için doğru olmadığını öne sürdü ancak nasıl olduğunu göstermekte başarısız oldu.[15] Lord Rayleigh daha radikal bir görüş ile ortaya atıldı. Ona göre hem eşbölüşüm teoremi hem de termal dengenin deneysel varsayımı doğrudur. Bu ikisini uzlaştırmak için eşbölüşüm teoreminin yıkıcı basitliğinden kaçışı sağlayacak yeni bir prensibe ihtiyaç duyulduğunu belirtti.[16] Albert Einstein 1907'de kuantum etkisi sebebiyle olan bu özgül ısıdaki anormallikleri göstererek kaçışı buldu.

Uygulamaları

İdeal gaz yasası

İdeal gazlar eşbölüşüm teoreminin önemli bir uygulamasını oluşturur. Parçacık başına ortalama kinetik enerji formülü:

${\displaystyle {\begin{aligned}\langle H^{\mathrm {kin} }\rangle &={\frac {1}{2m}}\langle p_{x}^{2}+p_{y}^{2}+p_{z}^{2}\rangle \\&={\frac {1}{2}}{\biggl (}{\Bigl \langle }p_{x}{\frac {\partial H^{\mathrm {kin} }}{\partial p_{x}}}{\Bigr \rangle }+{\Bigl \langle }p_{y}{\frac {\partial H^{\mathrm {kin} }}{\partial p_{y}}}{\Bigr \rangle }+{\Bigl \langle }p_{z}{\frac {\partial H^{\mathrm {kin} }}{\partial p_{z}}}{\Bigr \rangle }{\biggr )}={\frac {3}{2}}k_{B}T\end{aligned}}}$

olmak üzere, eşbölüşüm teoremi klasik mekanikten ideal gaz yasasının türetilmesinde kullanılır. q = (q_x, q_y, q_z) ve p = (p_x, p_y, p_z) gazdaki bir parçacığın konum ve momentum vektörü ve F de parçacığa uygulanan net kuvvet olsun;

${\displaystyle {\begin{aligned}\langle \mathbf {q} \cdot \mathbf {F} \rangle &={\Bigl \langle }q_{x}{\frac {dp_{x}}{dt}}{\Bigr \rangle }+{\Bigl \langle }q_{y}{\frac {dp_{y}}{dt}}{\Bigr \rangle }+{\Bigl \langle }q_{z}{\frac {dp_{z}}{dt}}{\Bigr \rangle }\\&=-{\Bigl \langle }q_{x}{\frac {\partial H}{\partial q_{x}}}{\Bigr \rangle }-{\Bigl \langle }q_{y}{\frac {\partial H}{\partial q_{y}}}{\Bigr \rangle }-{\Bigl \langle }q_{z}{\frac {\partial H}{\partial q_{z}}}{\Bigr \rangle }=-3k_{B}T,\end{aligned}}}$

Buradaki, ilk denklem Newton'un ikinci yasasıdır ve ikinci sırada Hamilton denklemleri ve eşbölüşüm teoremii kullanılır. N parçacıklı bir sistem için,

${\displaystyle 3Nk_{B}T=-{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }.}$

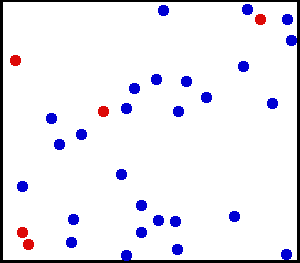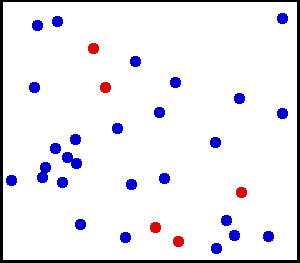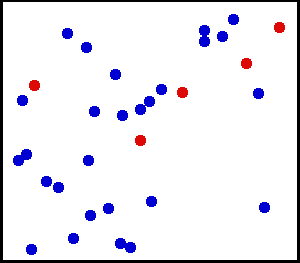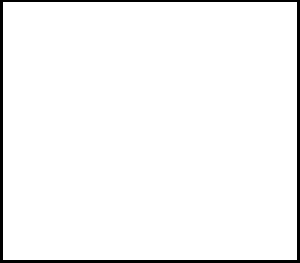
formülü sağlanır. Newton'un üçüncü yasası ve ideal gaz varsayımı ile sisteme uygulanan net kuvvet kabın duvarlarının uyguladığı kuvvettir, ve bu kuvvet gazın P basıncı ile verilir. Dolayısıyla

${\displaystyle -{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }=P\oint _{\mathrm {surface} }\mathbf {q} \cdot \mathbf {dS} ,}$

sonucuna ulaşılır. Buradaki dS kabın duvarları boyunca sonsuz küçük alan elemanıdır. Konum vektörünün diverjansı q,

${\displaystyle {\boldsymbol {\nabla }}\cdot \mathbf {q} ={\frac {\partial q_{x}}{\partial q_{x}}}+{\frac {\partial q_{y}}{\partial q_{y}}}+{\frac {\partial q_{z}}{\partial q_{z}}}=3,}$

olduğundan diverjans teoremi

${\displaystyle P\oint _{\mathrm {surface} }\mathbf {q} \cdot \mathbf {dS} =P\int _{\mathrm {volume} }\left({\boldsymbol {\nabla }}\cdot \mathbf {q} \right)dV=3PV,}$

olarak ifade edilir. Buradaki dV kab içindeki sonsuz küçük hacim elemanı ve V kabın toplam hacmidir.

Bu eşitliklerin bir araya getirlimesiyle

${\displaystyle 3Nk_{B}T=-{\biggl \langle }\sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}{\biggr \rangle }=3PV,}$

elde edilir. Bu da N parçacık için ideal gaz yasasını ifade eder:

${\displaystyle PV=Nk_{B}T=nRT,\,}$

Buradaki n = N/N_A mol sayısı ve R = N_Ak_B de gaz sabitidir. Eşbölüşüm ideal gaz yasası ve iç enerjinin türetilmesini bastitçe sağlıyor olsa da aynı sonuç alternatif bir yöntem olan bölüşüm fonksiyonunun kulanılmasıyla da elde edilebilir.[17]

Notlar

1. • Brush, S.G. (1976). The Kind of Motion We Call Heat, Volume 1. Amsterdam: North Holland. ss. 134-159. ISBN 978-0-444-87009-4.
   • Brush, S.G. (1976). The Kind of Motion We Call Heat, Volume 2. Amsterdam: North Holland. ss. 336-339. ISBN 978-0-444-87009-4.
   • Waterston, J.J. (1846). "On the physics of media that are composed of free and elastic molecules in a state of motion". Roy. Soc. Proc. Cilt 5. s. 604. doi:10.1098/rspl.1843.0077.(abstract only).
   • Not published in full until "On the Physics of Media that are Composed of Free and Perfectly Elastic Molecules in a State of Motion". Philos. Trans. R. Soc. London. Cilt A183. 1893. ss. 1-79. doi:10.1098/rsta.1892.0001.
   • Reprinted J.S. Haldane, (Ed.) (1928). The collected scientific papers of John James Waterston. Edinburgh: Oliver & Boyd.
   • Waterston, JJ (1843). Thoughts on the Mental Functions. (reprinted in his Papers, 3, 167, 183.)
   • Waterston, JJ (1851). "21st meeting, Transactions of the Sections". British Association Reports. Cilt 21. s. 6.
   Waterston's key paper was written and submitted in 1845 to the Royal Society. After refusing to publish his work, the Society also refused to return his manuscript and stored it among its files. The manuscript was discovered in 1891 by Lord Rayleigh, who criticized the original reviewer for failing to recognize the significance of Waterston's work. Waterston managed to publish his ideas in 1851, and therefore has priority over Maxwell for enunciating the first version of the equipartition theorem.
2. Maxwell, JC (2003). "Illustrations of the Dynamical Theory of Gases". WD Niven (Ed.). The Scientific Papers of James Clerk Maxwell. New York: Dover. Vol.1, pp. 377-409. ISBN 978-0-486-49560-6. Read by Prof. Maxwell at a Meeting of the British Association at Aberdeen on 21 September 1859.
3. Boltzmann, L (1871). "Einige allgemeine Sätze über Wärmegleichgewicht (Some general statements on thermal equilibrium)". Wiener Berichte. Cilt 63. ss. 679-711. (Almanca) In this preliminary work, Boltzmann showed that the average total kinetic energy equals the average total potential energy when a system is acted upon by external harmonic forces.
4. Boltzmann, L (1876). "Über die Natur der Gasmoleküle (On the nature of gas molecules)". Wiener Berichte. Cilt 74. ss. 553-560. (Almanca)
5. Petit, AT (1819). "Recherches sur quelques points importants de la théorie de la chaleur (Studies on key points in the theory of heat)". Annales de Chimie et de Physique. Cilt 10. ss. 395-413. (Fransızca)
6. Pais, A (1982). Subtle is the Lord. Oxford University Press. ISBN 0-19-853907-X.
7. Dewar, J (1872). "The Specific Heat of Carbon at High Temperatures". Philosophical Magazine. Cilt 44. s. 461.
   Weber, HF (1872). "Die specifische Wärme des Kohlenstoffs (The specific heat of carbon)". Annalen der Physik. Cilt 147. ss. 311-319. (Almanca)
   Weber, HF (1875). "Die specifische Wärmen der Elemente Kohlenstoff, Bor und Silicium (The specific heats of elemental carbon, boron, and silicon)". Annalen der Physik. Cilt 154. ss. 367-423, 553-582. (Almanca)
8. de la Rive, A (1840). "Quelques recherches sur la chaleur spécifique (Some research on specific heat)". Annales de Chimie et de Physique. Cilt 75. ss. 113-144. (Fransızca)
   Regnault, HV (1841). "Recherches sur la chaleur spécifique des corps simples et des corps composés (deuxième Mémoire) (Studies of the specific heats of simple and composite bodies)". Annales de Chimie et de Physique. Cilt 1 (3me Série). ss. 129-207. (Fransızca) Read at l'Académie des Sciences on 11 January 1841.
   Wigand, A (1907). "Über Temperaturabhängigkeit der spezifischen Wärme fester Elemente (On the temperature dependence of the specific heats of solids)". Annalen der Physik. Cilt 22. ss. 99-106. (Almanca)
9. Kundt, A (1876). "Über die specifische Wärme des Quecksilbergases (On the specific heat of mercury gases)". Annalen der Physik. Cilt 157. ss. 353-369. (Almanca)
10. Wüller, A (1896). Lehrbuch der Experimentalphysik (Textbook of Experimental Physics). Leipzig: Teubner. Vol. 2, 507ff. (Almanca)
11. Eucken, A (1912). "Die Molekularwärme des Wasserstoffs bei tiefen Temperaturen (The molecular specific heat of hydrogen at low temperatures)". Sitzungsberichte der königlichen Preussischen Akademie der Wissenschaften. Cilt 1912. ss. 141-151. (Almanca)
12. Maxwell, JC (1890). "On the Dynamical Evidence of the Molecular Constitution of Bodies". WD Niven (Ed.). The Scientific Papers of James Clerk Maxwell. Cambridge: At the University Press. Vol.2, pp.418-438. ISBN 0-486-61534-0. ASIN B000GW7DXY. A lecture delivered by Prof. Maxwell at the Chemical Society on 18 February 1875.
13. Kittel, C (1996). Introduction to Solid State Physics. New York: John Wiley and Sons. ss. 151-156. ISBN 978-0-471-11181-8.
14. Boltzmann, L (1895). "On certain Questions of the Theory of Gases". Nature. Cilt 51. ss. 413-415. doi:10.1038/051413b0.
15. Thomson, W (1904). Baltimore Lectures. Baltimore: Johns Hopkins University Press. Sec. 27. Re-issued in 1987 by MIT Press as Kelvin's Baltimore Lectures and Modern Theoretical Physics: Historical and Philosophical Perspectives (Robert Kargon and Peter Achinstein, editors). ISBN 978-0-262-11117-1
16. Rayleigh, JWS (1900). "The Law of Partition of Kinetic Energy". Philosophical Magazine. Cilt 49. ss. 98-118.
17. L. Vu-Quoc, Configuration integral (statistical mechanics) 28 Nisan 2012 tarihinde Wayback Machine sitesinde arşivlendi., 2008.