Göreli Doppler etkisi
Relativistik Doppler Etkisi ya da Göreli Doppler etkisi (veya Doppler Olayı), adını ünlü bilim insani ve matematikçi Christian Andreas Doppler`dan almakta olup, kısaca dalga özelliği gösteren herhangi bir fiziksel varlığın frekans dalga boyu Dalga boyu, bir dalga görüntüsünün tekrarlanan birimleri arasındaki mesafedir. Yaygın olarak Yunanca lamda (λ) harfi ile gösterilmektedir. hareketli (``yakınlaşan veya uzaklaşan``) bir gözlemci tarafından farklı zaman ve/veya konumlarda farklı algılanması olayıdır. Bu da göreli olduğunu belirtir. Herhangi bir ``A`` konumundan ``B`` konumuna gitmek icin fiziksel bir dalga ortamı`na ihtiyaç duyan dalgalar (``örneğin. ses dalgalari veya su dalgalari``) icin Doppler Etkisi hesaplamaları yapılırken, dalga kaynağı ve gözlemcinin birbirine gore konum, yön ve hızlarının yanında dalganın içinde veya üzerinde hareket ettiği dalga ortamının da fiziksel yapısı (yoğunluk, hacim, iletkenlik katsayısı, kimyasal özellikleri, vb.) dikkate alınmak zorundadır. Eğer söz konusu dalga herhangi bir ``A`` konumundan ``B`` konumuna gitmek için fiziksel bir dalga ortamına ihtiyaç duymuyor ise (``örneğin ışık, radyo dalgaları veya radyasyon``) Doppler Etkisi hesaplamalarında sadece dalga kaynağının ve gözlemcinin birbirine göre birim zamandaki konumlarının değerlendirilmesi yeterlidir. Göreli doppler olayı değişikliği olduğu frekansa (ve dalga boyu arasında) ışık kaynağının göreceli hareketine göredir ve (klasik olarak gözlemci tarafından açıklanan hesap etkileri içine çekerken özel görelilik kuramının nedeniyle göreli Doppler etkisi diye adlandırılır ), Göreli Doppler etkisi relativistik olmayan farklı Doppler etkisi denklemleri dahil olarak zaman genişlemesi etkisini özel görelilik ve referans noktası olarak yayılma ortamı dahil değildir. Lorentz simetri gözlenen frekanslar için toplam farkı anlatır.

Görüntüleme

Şekil 2'de , mavi nokta gözlemciyi temsil eder ve ok çevresine gözlemcinin hız vektörü akrabası temsil eder. Gözlemci sabit olduğunda, 'x ' , y ' - ızgara sarı görünür ve ' y ' ' - ekseni siyah dikey çizgi olarak görünür . Sağa Gözlemcinin hızı arttırmak renk ve [ ışık [ sapmaları ] ] ızgara bozan kaydırır. Gözlemci (sağ ızgara üzerinde ) öne baktığında , puan , yeşil , mavi , mor ve ( Blueshift ) görüntülenir ve ızgara çizgileri uzaklaştırın görünür . Gözlemci ( ızgara üzerinde sol ) geriye görünüyorsa , o zaman noktaları görünür kırmızı ( [ [ kırmızıya kayma ] ] ) ve çizgiler birbirine yaklaştırın görünür . Izgara değişmedi , ancak gözlemci için ' görünümü ' vardır.
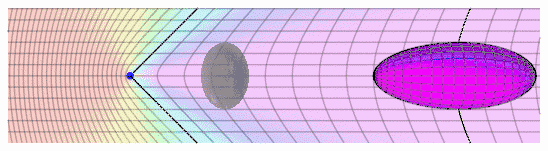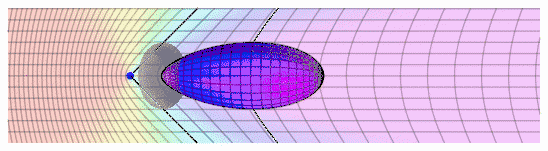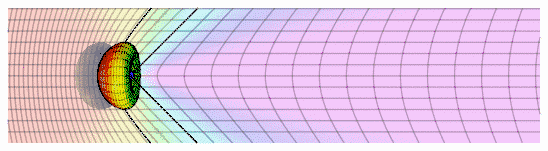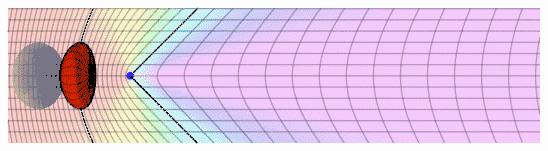
Diyagram 3 ızgara bozulma gözlemci veya uzakta doğru hareket eden bir nesne için aynı temel [ [ Lorentz daralmasını ] ] ayrı bir göreli optik etkisi olduğunu göstermektedir .
Doppler Etkisi konusunda bilinmesi gereken en önemli husus, her ne kadar gözlemci dalga frekansinin kendi hareketi ya da dalga kaynağinin hareketi yüzünden değiştiğini görse de, aslında frekansin sabit kaldiği gerceğidir. Tam olarak ne olduğunu daha iyi anlamak icin şöyle bir örnek üzerinde düşünelim: Siz yerinizde ve hareketsizsiniz. Bir arkadaşiniz sizden 10 metre uzakta duruyor ve size her saniyede bir elindeki tenis toplarindan birini firlatiyor. Burada arkadasinizin toplari her seferinde ayni dogru boyunca ve aynı hızda attiğini varsayalım. Eğer arkadaşınız da hareketsiz ise her saniyede bir 10 metre yol kateden tenis toplarından biri size ulaşacaktır. Şimdi arkadasinizin yine her sahinyede bir top firlattigini (``yani aslinda top firlatma frekansi degismiyor``), ancak bu sefer size dogru yurumeye basladigini ongorelim. Bu durumda size ulasan iki top arasindaki sure 1 saniyeden daha kisa olacaktir cunku toplar her seferinde 10 metre, 9 metre, 8 metre seklinde daha az mesafe katettikten sonra size ulasacaktir. Elbette ayni etkinin zitti arkadasiniz sizden uzaklasirken de gecerli olacaktir. Bir baska degisle, toplar arkadasinizin elinden her zaman saniyede bir ciktigi halde, sizin ya da arkadasinizin hareketi yuzunden size azalan ya da artan zamanlarda ulasacaktir. Bu da dogal olarak arkadasinizin size topu farkli zamanlarda firlattigini dusunmenize sebep olur. Yani aslinda Doppler Etkisi`nde "etkilenen" asil fiziksel degisken dalga boyu`dur. Elbette dalga boyu ile frekans ters orantili oldugundan gozlemciye gore dalga kaynaginin frekansi da degisiyor gibi gorunur.
Karşılaştırma
Göreli Doppler etkisini anlamak için Doppler etkisi , [ [ zaman genişleme ] ] ve [ ışık ] ve [ sapmaları ] anlamayı gerektirir . Doppler etkisi , basit bir benzetme olarak yakalambaç oynayan iki kişi düşünün . Hala ayakta olan bir alıcı saniyede bir metre de ( Hz 1 & nbsp ) sabit bir sürahi her saniye bir top fırlattığını düşünün. ( Hz 1 & nbsp ) sabit tutucu saniyede bir top alacaksınız. Sonra alıcı saniyede 0.5 metre uzakta sürahi yürüyor ve bir topu yakalar her 2 saniyede (0.5 & nbsp; Hz) . Son olarak, alıcı üç topları her iki saniyede ( Hz 1.5 & nbsp ) saniyede 0.5 metre sürahi doğru yürür ve yakalar . Atıcı doğru veya uzak tutucu taşındı , aynı doğru olurdu . Benzetme , göreli Doppler etkisi yayıcısı olarak ışığın frekansını değiştirir veya gözlemci doğru veya uzakta başka hareket eder .
Sapma etkisini anlamak için , yine ters yönde hareket eden iki paralel konveyör bantlar ( kaldırımlar hareketli ) mandalı oynayan iki kişi düşünün. Sürahi hızı ve kemerler aralık ve nerede alıcı olduğunu bağlı olarak farklı amaçlamalıdır. Yakalayıcı sürahi gelen topları farklı bir açıyla attıkları görülür. Topun hızına sürahi alıcı hattı ve göreli hız vektörü , ve 2) sürahi alıcı hızı göreceli arasında 1) anlık açı : Bu açı değişiklikleri bağlıdır. Benzetme , ışığın sapmasına bağlıdır: 1) yayıcı - gözlemci hattı ve göreli hız vektörü , ve 2) ışık hızına yayıcı - gözlemci hızı göreceli arasındaki anlık açı .
Görüş hattı boyunca hareket
Gözlemci ve kaynak göreli bir hız ile birbirinden ' ' uzak ' ' hareket ediyor varsayalım ( negatif ise gözlemci ve kaynak) birbirlerini hareket halinde görürler . Referans çerçevesi sorunu göz önüne alındığında kaynaklardan çıkan bir ön dalga gözlemciye ulaşır varsayalım . Bir sonraki dalga gözlemciden bir mesafe daha sonra meydana gelir. ( dalga boyu, Kaynaktan yayılan dalga , ve ışık hızı.
Wavefront hızı ile hareket , ama aynı zamanda gözlemci hızıyla uzaklaşıyor , so . Bu bize bunu verir
is [[beta (velocity)| ışık hızı açısından gözlemcinin hızı.
Göreli [ [ zaman genişlemesi ] ] nedeniyle , gözlemciye göre bu zaman şu şekilde ölçülecektir.
- Lorentz çarpanıdır. Ve buna karşılık gözlenen frekans da;
Oransal olarak,
gözlemci, kaynak göreli olduğunda Doppler çarpanı denir. Bu terminoloji konusu özellikle yaygındır.
Ve elde edilen kırmızıya kayma;
şeklinde de yazılabilir.
Relativistik olmayan limitte kırmızıya kayma (yani; olduğunda) bu kırmızıya kayma yaklaşık olarak elde edilir
Klasik Doppler etkisine göre böyle kabul görmektedir.
Eylemsizlik içinde olan gözlemciler için sistematik türevini alma
[ | Lorentz denklemleri ] [ Lorentz dönüşümü ] kendilerini relativistik olmayan dalgalar için bir göreli Doppler kayması denklemini türetmek için açıkça kullanılabilir ve daha iyi göstermek amacıyla daha sistematik bir türevi tekrar etmek gerekir.
İki tane eylemsiz referans sistemi olduğunda, ve , eksenler şu şekilde inşa edilir ve rastlantısal olarak , where zamanı ölçüldüğü üzere ve zamanı ölçüldüğü üzere . harekete bağıl olarak sabit hızla ; genelliği kaybetmeden, Bu hareket sadece X ekseni boyunca yönlendirilmesi alacaktır. Böylece, Lorentz dönüşümü denklemleri şeklinde olacaktır.
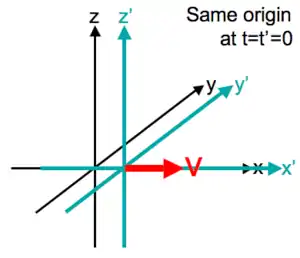
bakınız hız ekleme formülü , ve , ve ışık hızıdır
Türev gözlemcinin 'yi önemsiz gibi gözükse de ne şekilde gördüğü ile başlar ve görür. Bir sinyal kaynağını orijinde durağan konumlandırılmış hayal edebiliriz, orijindir ve de sistemdir. Biz ilk zaman ilk etkiyi üretmek için bu sinyal kaynağını alacağız. (bu olay 1 olsun) ve ikinci etki de (bu da olay 2 olsun), gözlemci olarak sinyal kaynağının frekansı şu şekilde görünür. Biz o zaman sadece gözlemci olarak zaman ve nerede olduğunu görmek için Lorentz dönüşümü denklemlerini kullanırız. şu şekilde görünür ve şu iki olay gerçekleşir:
| Observer in | Observer in | |||||
|---|---|---|---|---|---|---|
| Event 1 |
|
| ||||
| Event 2 |
|
|
Etkiler arasında ölçülen period gözlemcisi tarafından yapılır, ama de olay 2 meydana gelir. Olay 1 için uzayda farklı bir noktada görüldüğü gibi gözlemcisi tarafından gözlenir (yani, olduğu durumda) — seyahat etmek için 'den 'e şeklinde etkinin zamana göre faktörünü almalıyız. Bu Doppler etkisini nihai nedenidir ve ayrıca klasik yöntemde de mevcuttur : Bu komplikasyonun doğada relativistik olmadığını hatırlamak gerekir. Bu geçiş süresi farkına eşittir ve etkinin hızı ile bölünen gözlemcisi bunu görür. Eğer etki bir hızla hareket ederse de olur (negatiftir çünkü negatif x ekseni yönünde hareket eder orijindeki gözlemcidir ), daha sonra etkinin hızı gözlemci a’ ya doğru olur t , şeklinde görür:
Yukarıda, hızlar için Lorentz denklemleri kullanılmıştır. Böylece, etkiler arası periyot süresi gözlemcisi için şu şekilde ölçülür:
ile ve sabit sıklığı açısından ' herhangi ' hareketli bir dalga bize göreli Doppler kaymasını verir istenilen sonucu almak için sadeleştirmesi yapılır, :
Eğer bu formülü uygularsak or (eşitlikte ) relativistik etkiler ihmal edilebilir ve bu formül bize Doppler etkisinin formülünü verir.
Elektromanyetik radyasyon için formülü şu şekildedir:
ya da dalga boyu açısından:
orijinde kaynağının dalga boyu orijindir ve de bu orijin noktasındaki gözlemcidir. Bu denklemlerde v (ve dolayısıyla β) yaklaşırken , kaynak gözlemciden uzaklaştığı zaman pozitif sayılır ve kaynak gözlemciye yakınlaştığı zaman negatif olduğunu belirtir.
Elektromanyetik radyasyon, klasik mekaniğin sınırı için, , öğreticidir. Doppler etkisi formülü basit hale indirgenebilir . Bu deneyde açıkça bir anlaşmazlık olmasına rağmen, bu klasik mekanik için doğru sonuçtur. Klasik mekanik etkileşim maksimum hızı bakımından doğrudur [note 1] — Elektrodinamik için , ışık hızı - sonsuz olması . Dalga kaynağı önceki dalgalar gözlemci karşılaşırsanız zaman taşımak için zaman vardır , çünkü klasik ya da göreli Doppler etkisi ortaya çıkar. Bu sonraki dalgalar daha uzağa yayılan ( veya yakın) gözlemci için kaynak hareket olmasa da başka türlü olurdu anlamına gelir. Bunun etkisi gözlemci onları karşılaşır olarak dalga boyu germek ( ya da sıkıştırmak ) gerekmektedir. Ancak dalgalar anında seyahat ediyorsanız dalgalar geç ya da erken onlar anında gelmesi zaten beklendiğinden daha gözlemci gelmesiyle birlikte, kaynak (yakın veya) daha uzak olması hiç fark etmez . Böylece, klasik mekanik görecelik kuramının doğru cevap verir ise deney tarafından doğrulandığı gibi , ışık dalgalarının hiçbir Doppler etkisi olmaması gerektiğini öngörür.[1]
Görelilik ilkesinde Mutlak dinginlik (hareketsizlik) yoktur. Bütün hareketler ya da hareketsizlikler, gözlenen bir başka nesneye görelidir. Bir cismin dingin halde mi, yoksa düzgün doğrusal hareket mi yaptığı mekanik deneylerle ayırt edilemez. Başka bir deyişle, bir referans noktasına göre sabit duran bir gözlemci ile o referans noktasına göre düzgün doğrusal hareket eden başka bir gözlemci, bütün hareket yasalarını aynı algılarlar. Gözlemcilerin hızlarına bağlı olmaksızın fizik yasaları her eylemsiz sistemde aynıdır.
Işık hızı sabittir ve gözlemcilerin birbirlerine göre hızları ne olursa olsun, ışık hızı bütün gözlemciler için aynıdır.
Enine Doppler etkisi
Gökbilimde, özellikle evrenin genişlemesi konularında sıkça duyduğumuz bir terimdir ‘’Kırmızıya Kayma’’. Peki, nedir bu? Bunu anlayabilmeniz için önce ‘’elektromanyetik spektrum (tayf)’’ hakkında bilgi sahibi olmanız gerekir.
Doppler etkisi yalnız seste değil ışık dalgalarında da görülür. Bu etkinin en önemli sonuçlarından biri de astronomide "kırmızıya kayma" ya da "maviye kayma" olarak bilinen olgudur. Renkli görmemizin nedeni gözümüzün değişik dalga boylarındaki, yani frekanslardaki ışıklara değişik tepki vermesidir. Hareketli bir kaynaktan gelen sesin frekansı duran bir gözlemci için nasıl değişiyorsa, yıldızlardan gelen ışığın dalga boyu da yıldızın hareketine bağlı olarak değişecektir. Bu nedenle astronomlar, Güneş Sistemi'ne yaklaşan ya da ondan uzaklaşan yıldızların ve gökadaların hızını ölçmek için Doppler etkisinden yararlanırlar. Tıpkı ses örneğinde olduğu gibi, yaklaşan bir yıldızın ışığı duran bir yıldızın ışığından daha yüksek frekansta, başka bir deyişle daha kısa dalga boyunda gelecektir. Görünür ışığın tayfında en kısa dalga boylarının yer aldığı uçta mavi bulunduğundan, söz konusu yıldızın ışığı gözümüze daha mavi görünür. Öte yandan, uzaklaşan bir yıldızın ışığı duran bir yıldızın ışığından daha alçak frekansla, yani daha uzun dalga boyuyla yeryüzüne ulaşır. Görünür ışığın tayfında en uzun dalga boylarının yer aldığı uçta kırmızı bulunduğundan, uzaklaşan yıldızlar da daha kırmızı olarak görünür. Yıldızların yapısındaki kimyasal elementlerin o yıldızın tayfında oluşturduğu çizgiler normalde bulunmaları gereken yerden başka yere kaymış oldukları için, Doppler etkisinden ileri gelen bu olaya kırmızıya ya da maviye kayma denir. Gerçekten de bu çizgiler yaklaşan yıldızların ışığında tayfın mavi ucuna, uzaklaşan yıldızlarda ise kırmızı ucuna doğru kaymıştır. Bu çizgiler normal konumlarının ne kadar dışına kaymışsa, o gökcismi de o kadar hızlı yaklaşıyor ya da uzaklaşıyor demektir. Kuvazar denen bazı gökcisimlerinde kırmızıya kayma o kadar büyüktür ki, tayfın morötesi bölümünde bulunması gereken çizgiler görünür ışığın yeşil bölümüne kaymıştır. Bu da kuvazarların neredeyse ışık hızıyla bizden uzaklaştığını gösterir. Işık, fotonlardan meydana gelir. Boşlukta ışık hızına ulaşan bu fotonlar hem parçacık hem dalga özelliği sergilerler. Bu dalganın uzunluğuna göre kendisini sınıflandırırız. Elektromanyetik Spektrum dediğimiz tablo ise bu sınıflandırmayı içerir. Siz bu yazıyı okurken bilgisayarınız ya da cep telefonunuz görebildiğimiz dalgaboyunun dışında ışık yayarlar. Elektromanyetik Spektrum gama ışınlarından, radyo dalgalarına kadar bilinen tüm elektromanyetik dalgaları içeren bir tablodur. Görünür ışık tayfı, bu spektrumun bütünü içerisinde çok küçük bir alanı kapsar. Gözlerimiz ile ortalama 380-740 nanometre arası dalgaboyunu algılayabiliriz. Şimdi tekrar ‘’Kırmızıya Kayma’’ konusuna dönelim. Bir gözlemci, hareketli bir kaynaktan gelen frekans ve dalgaboyunu farklı algılar. Buna Doppler Etkisi diyoruz. Bir ışık, gözlemci ve ışık kaynağının hareketine bağlı olarak çeşitli dalgaboylarında gözlenir. Işık bize yaklaşıyorsa ışığın dalgaboyu kısalır bu maviye kaymadır. Eğer ışık bizden uzaklaşıyorsa dalga boyu uzar bu da kırmızıya kaymadır. Doppler Etkisi ses dalgaları için de geçerlidir. Bunu şöyle betimleyebiliriz. Uzaktaki bir araba, yakınımızda ki bir arabaya göre daha pes bir ses çıkarır. Yani gözünüze uzaktaki bir arabayı kestirin, bu arabanın sesi bize yaklaştıkça tizleşecektir.
Kütlesel çekim alanı, ışığın yalnız doğrultusunu değil, dalga boyunu (dolayısıyla frekansını) da değiştirir. Kütleçekimi altında cisme doğru gelen ışık demetinin dalga boyu azalır (frekansı artar), ışık, mavi görünür. Kütleçekiminden uzaklaşarak gelen bir ışık demetinde ise dalga boyu artar (frekans küçülür), ışık, kırmızı görünür.Birçok galaksinin hızı ölçüldü ve Tayf çizgilerinin, tayfın kırmızı ucuna doğru kaydıkları görüldü. Kırmızıya kayma denen bu olay, galaksilerin bizden uzaklaştığını gösteriyordu. Bilim adamları, daha uzak galaksilerin hızlarının daha büyük gözüktüğünü buldular. Kırmızıya kayma, gözlenebilen en uzak galaksilerinki saniyede 60 bin kilometre ve daha büyük hızlarda olmak üzere, galaksilerin gerçekten birbirinden uzaklaşmakta olduğunu kanıtladı. Peki, bunu astrofizikte nasıl mı kullanıyoruz. Bu astrofizikte bizim en önemli araçlarımızdan birisidir. Edwin Hubble bu yöntemi kullanarak çok büyük keşiflere imza attı. Işık tayflarını inceleyerek evrenin durağan olmadığı, gökadaların birbirinden hızla uzaklaştığını fark etti. Bu evrenin genişlediği anlamına geliyordu. Bugün hala bu yöntemi kullanarak gökcisimlerinin bizden uzaklıklarını, uzaklaşma hızlarını, Güneş atmosferindeki gaz yükseltilerinin ve çift yıldızların hızlarını ölçebiliyoruz. Vakti zamanında Satürn’ün halkalarının hızlarını ölçmek için bile kırmızıya kaymayı kullandık. Nesneler hızlandırılmış değildir varsayarsak , ışık nesneler birlikte en yakın bir süre sonra alınacak olduğunda yayılan . kırmızıya kayma miktarı ölçülür.
Objeler birbirlerine yakın olduğu zaman ışık alınırsa , o zaman daha önce bir süre çıkışı olmuştur. Maviye kayma miktarı ölçülür.
İki duruma göre de hareketleri bağlıdır klasik teori için, bu iki durumda da için özel bir tahminde bulunmak mümkün değil.
Enine Doppler etkisi göreli Doppler etkisi bir sonucudur.
Alıcının çerçevesinde, θ0 emisyon de damlatıcının yönünde ve resepsiyonda ışığın gözlenen yönü arasındaki açıyı temsil eder. Ne durumda θ0 = π/2, Işık yakın yaklaşım şu anda yayılan ve bir enine kırmızıya kayma elde edildi.
Enine Doppler etkisi , özel teorisinin ana tahminlerinden biridir. Einstein 1907 yılında söylediği gibi : Alınan frekans aynı faktörle azalır , böylece özel görelilik göre hareket nesnenin yaydığı frekans , Lorentz faktörü azalır.
Karşıtlık
Bazen soru enine Doppler etkisi verici ile hareket eden başka bir gözlemci iken " gözlemci " tarafından görülen bir kırmızıya kayma neden olabilir nasıl ortaya çıkması olur de alıcıdan (belki yanlışlıkla) gönderilen bir ışık kırmızıya kaymaya başlar.
Bu kavram "enine" karşılıklı olmadığını anlamak için gereklidir. Her katılımcı kişinin dinlenme çerçevesinin cinsinden ölçülen hafif enine onları ulaştığında diğer kişinin dinlenme çerçevede ölçülen diğer sonra ışık yayılan olduğunu anlar . Buna ek olarak , her bir katılımcı azaltılmış olarak diğer frekans ölçer ( " zaman genişlemesi " ) . Bu etkiler , böylece görelilik prensibini uyarak , gözlemler tamamen karşılıklı olur .
Görelilik teorisi'nde, zaman genişlemesi birbirlerine ya da farklı yerçekimli kitleler, yer göreli hareket ya da gözlemciler olarak ölçülen olaylar arasında geçen zaman gerçek bir farktır. İkinci bir gözlemcinin kendi eşit doğru saati ile karşılaştırıldığında, istirahatteki bir gözlemciye göre doğru bir saat farklı bir oranda ölçülebilir. Bu etki ne saatlerin teknik yönden ne de sinyalleri yaymak için zamana ihtiyacımız olduğu gerçeğinden, fakat uzay-zamanın kendi doğasından doğar. Bazen büyük bilimsel bulgulara, o buluşun anlamını saptıracak talihsiz adlar verilir. “Görelilik” de bunlardan biridir. “Her şey görelidir” deyince, Einstein’in büyük hayali çoğunlukla yanlış anlaşılıyor. Sanki ortada “doğru” bir şey yok, herkes kendi bakış açısını “doğru” imiş gibi ortaya sürmekte özgürdür gibisine yanlış bir izlenim doğuyor. Oysa Einstein, bunun tam tersini yaptı. O fizik kurallarının evrenselliğini, bakış açısına göre değişmezliğini gösterdi. Önceki bölümde anlatıldığı gibi, görelilik kavramının doğuşu Einstein’dan çok öncedir. En azından Galilei’ye kadar geriye götürebiliriz. Newton, görelilik kavramını bilinçle kullanmış ve hareket yasalarını mutlak uzay ve mutlak zamana göre ifade etmiştir. Einstein’in özel görelilik kuramının Galilei ve Newton göreliliğinden farkı, uzayın ve zamanın mutlak olamayacağını söylemesidir. Matematiksel açıdan bakınca, Galilei dönüşümleri yerine Lorentz dönüşümünü kullanması ve çıkan sonuca yepyeni bir fiziksel yorum getirmesidir. Tabii, şimdi basitçe ifade ettiğimiz bu iş, o gün için hayal edilmesi zordu ve Einstein’in bu büyük hayali 20. yüzyıl başlarında fiziğe bakışımızı bütünüyle değiştiren büyük bir bilimsel bulgudur. Konuya girmeden önce, kısaca söylemek gerekirse, Özel Görelilik kuramı, fizik yasalarının eylemsiz konuşlanma sistemlerinde aynı olduğunu söyler. Sonuç çıkmamasını bu gün doğal karşılıyoruz, çünkü mutlak uzay ve mutlak zaman kavramlarına dayalı çözüm getirilemezdi. Başka bir deyişle, ortaya çıkan sorunların Newton Mekaniği ile çözülebilmesi olanaksızdı.
Çözüm yönünde ilk doğru adımı Lorentz attı. İkinci önemli adım ise, zamanın ünlü matematikçisi Poincare’den geldi. Bu ikisi, birbirlerinden bağımsız olarak, Görelilik Kuramı için gerekli bütün matematiksel araçları ortaya koymuşlardı. Ama onlar ortaya koydukları matematiksel formüllere fiziksel anlam veremediler.
Onları yorumlayıp, evrene bakışımızı değiştiren kuramı ortaya atan Albert Einstein oldu. 1905 yılında Özel Görelilik kuramını ortaya koydu. Bu kuramda Einstein, fizik yasalarının bütün eylemsiz sistemlerde aynı olduğunu gösterdi. Ama bu önemli sonuç onun için yeterli değildi. Fizik yasaları evrensel ise, eylemsiz sistemlerde olduğu gibi, eylemli sistemlerde de aynı olmalıydı. Bunun için gravitasyonu yaratan nedeni bulması gerekiyordu. Bunu bulması tam 10 yılını aldı. 1915 yılında da Genel Görelilik kuramını ortaya koydu. Bu iş, 1800 yıllık Aristo evren modelini 1543 yılında Copernicus’un yıkışından çok daha görkemli oldu.
Lorentz Dönüşümü'nden sezinlenebileceği gibi, t=t' gibi basit bir bağıntı olmayacağına göre zaman göreli bir kavram halini almaktadır. Gerçekte bunun anlamı eşanlılık kavramının hangi eylemsiz konuşlanma sistemi içinde olduğumuza bağlı olduğudur. Bu durum, ışık hızının hangi eylemsiz konuşlanma sistemi içinde olduğumuza bağlı olmadığından çıkar.
Hareket halindeki bir tren vagonunun tam ortasında bir lamba olsun. Lamba yandığında ışık hüzmesi hem trenin gidiş yönüne hem onun ters yönüne c=3×108m/sn hızıyla yayılacaktır.
Vagonun içindeki bir gözlemci, ışığın vagonun önüne ve arkasına aynı anda (eşanlı) ulaştığını görecektir.
Öte yandan, tren dışındaki bir gözlemci için durum farklıdır. Işığın hızı, gözlemcinin içinde bulunduğu eylemsiz sisteme bağlı olmaksızın, her gözlemciye göre aynıdır ve vagonun her iki yönüne doğru c hızıyla gider. Vagonun arkası kendisine doğru gelen ışığa yaklaşırken, vagonun önü kendisine doğru gelen ışıktan uzaklaşmaktadır. Dolayısıyla, ışık vagonun arkasına daha çabuk, vagonun önüne daha geç ulaşacaktır. Demek ki, bu iki olay, yerdeki gözlemci için eşanlı değildir.
Görüldüğü gibi, tren içindeki gözlemciye eşanlı görünen iki olay tren dışındaki gözlemciye farklı zamanlarda olan iki olay olarak görünmektedir.
Oyunu biraz daha eğlenceli kılmak için, trenden daha hızlı giden bir yarış arabası içindeki gözlemcinin olayları nasıl göreceğine bakalım.
Gene, ışığın hızının, gözlemcinin içinde bulunduğu eylemsiz sisteme bağlı olmaksızın, her gözlemciye göre aynı olduğunu ve vagonun her iki yönüne doğru c hızıyla gittiğini anımsayalım. Yarış arabası trenden daha hızlı olduğu için, arabadaki gözlemciye göre tren ters yönde gitmektedir. Dolayısıyla, vagonun önü kendisine doğru gelen ışığa yaklaşırken, vagonun arkası kendisine doğru gelen ışıktan uzaklaşmaktadır. Dolayısıyla, ışık vagonun arkasına daha geç, vagonun önüne daha erken ulaşacaktır. Demek ki, bu iki olay, arabadaki gözlemci için eşzamanlı değildir.
Relativistik Işıma doppler ışıması ya da doppler artması olarak da bilinir. Maddenin ışık hızına yakın bir hızda yayılan parlaklığını açıklayan bir işlemdir. Astronomi kaynaklarında, katılımlarla büyüyen sıkışık madde kökeninden gelen Relativistik jet plazmalarında Relativistik ışınma zıt yönlü meydana gelir. Katılımlarla büyüyen sıkışık madde ve Relativistik jetler sırayla gözlemlenmiş olan olayları açıklamayı hatırlatıyor. X ışını ikilisi, gama ışın patlaması ve etkin çekirdekli galaksi.( Kuasar katılımlarla büyüyen maddeyle ilişkilendirilebilir ama sadece etkin çekirdekli galaksinin bir çeşidi olarak düşünülürse.) Işıma, herhangi bir şeyin parlaklığını etkiler.Mesela deniz feneri ışık kaynağının görünümünü etkler. Işık kaynağı gemiye görünmez ya da sönük gelir eğer ışık kaynağı gemiye doğru ışımıyorsa ki o zaman çok parlak bir ışık olarak gemiden gözükür. Bu deniz feneri etkisi, Relativistik ışımada hareket yönünün ne kadar önemli olduğunu örnekler( gözlemciye göre). Eğer elektromanyetik radyasyon yayan az miktarda gaz gözlemciye doğru hareket ediyorsa durgun halinden daha parlak gelecektir. Eğer gaz gözlemciye doğru hareket etmiyorsa durgun halinden daha sönük gelecektir. Bu deniz feneri etkisinin önemi jetler tarafından tespit edilmiştir. M87 adlı galaksideki ikiz jetlerden biri dünyaya doğru diğeri ise ona zıt yönde giderken ışımanın nasıl görünümlerini etkilediğini gösterir. M87 nin dünyaya doğru hareket eden jeti teleskopla rahatça görülebilir ve ışıma yüzünden çok daha parlaktır. M87 deki diğer jet ise ışıma nedeniyle görünmeyecek kadar sönüktür.[1] 3C31 M87 den daha farklıdır çünkü her iki jet de görüş açımıza neredeyse 90 derece açıdadır ve bu nedenle aynı yoğunukta ışınlamaya maruz kalır. M87 dekinin aksine, 3C31 deki her iki jet de gözükür. Relativistik olarak hareket eden cisimler birçok fiziksel nedenden dolayı ışıma yapar. Işığın sapması, cismin hareket yönü boyunca çok sayıda fotonun yayılmasına neden olur. Doppler etkisi fotonların enerjisini değiştirir . Son olarak, cisim tarafından yayılan fotonların hareketi boyunca ölçülen zaman aralığı ile dünyada gözlemci tarafından ölçülen zaman farklıdır. Bunun nedeni ise, zaman genişlemesi ve fotonun geliş zamanı etkisinden dolayıdır. Tüm bu etkiler, Relativistik doppler etkisini tanımlayan denklemler tarafından belirtilen hareket eden cismin parlaklığını gösterir.( ki bu da neden doppler ışıması olarak da bilindiğini açıklar)
Işıktan Daha Hızlı Hareket
Eğer öncelik, eşanlılık ve sonralık kavramları gözlemciye göre değişiyorsa, bir olayın başka bir olayı yarattığı nedensellik (casuality) kavramını nasıl açıklayacağımızı ciddi olarak düşünmeliyiz.
Bunu biraz açıklamakta yarar vardır. Eğer bir A olayı başka bir B olayının olmasının nedeni ise, A olayı B olayından önce olmalıdır. Ama, bir gözlemci A olayının B olayından önce olduğunu, başka bir gözlemci ise A olayının B olayından sonra olduğunu gözlüyorsa, nedensellik konusunda bir uyuşmazlık ortaya çıkacaktır.
Sabit frekanslı ses üreten bir kaynaktan yayılan sesin, yayılması sırasında frekans değerinde bir değişiklik olmaz. Ancak ses kaynağı ya da ses algılayıcısı hareketli ise bu durum değişir. Ses kaynağının hareketli olması durumunda ya da sesi duyan kişinin hareketli olması durumunda sesin frekansı, kaynaktan çıkan frekanstan farklı olarak algılanır. Bu duruma seste doppler etkisi denir. Doppler olayında değişen dalga boyudur. Ancak dalga boyu ile frekans ters orantılı olduğundan, gözlemci dalga kaynağının frekansını da değişmiş gibi algılar. Doppler olayı hareketli kaynağın hızının ses hızından yavaş olduğu durumlarda gözlenir. Kaynak hareket etmiyorsa dalgalar kaynak etrafında simetriktir. Frekansı fK olan bir kaynak, özellikleri değişmeyen bir ortamda λ dalga boylu v hızıyla hareket eden dalgalar yayıyorsa;
Deneysel doğrulama
Uygulamada , enine etkisi deneysel doğrulama genellikle bakarak içerir boyuna yaklaşımı ve durgunluk için frekans veya hareket nedeniyle dalga boyu değişiklikler : Birlikte bu iki oranları karşılaştırarak klasik " ilişkilerini ekarte edebilir teori , bu tahminlerin daha " kızıl " ve gerçek ilişkiler olduğunu kanıtlamak " . Enine Doppler kayması özgü astrofizik nesne [ [ SS 433 ] ] yorumlanmasına merkezidir.
İlk uzunlamasına deneyler ( 1938 ) 'de [ [ Herbert E. Ives ] ] ve Stilwell tarafından yapılmıştır , ve diğer birçok uzunlamasına testler çok daha yüksek hassasiyetle beri yapılmıştır.[2] Ayrıca doğrudan enine deney aslında ' nesneye 90 derece ' amaçlayan ' bir dedektör için kırmızıya kayma efekti doğruladı.[3]
Rastgele bir yönde hareket
Eğer gözlemcinin referans noktasına göre bir kaynaktan çıkan hız ile uzaklaşmaktaysa ve açısı frekans değişiklikleri ( ışık yayıldığı zaman) gözlemciye gelen kaynağın yönüne göre;
- (1)
Belirli bir durumda ve enine Doppler etkisi elde edilebilir:
Ya da ışığın sonlu bir hızı nedeniyle foton varsayarsak , ışık ışını için gelen açı olarak gözlemci tarafından algılanan , farklı bir açıyla salınan kaynağının referans noktası içinde olduğu zaman . ve [ [ göreli sapma formülü ] ] ile birbirlerine bağlıdır:
Bu yüzden denklem 1 olarak yazılabilir.
- (2)
Örneğin, bir foton damlatıcının referans çerçevesinde dik açılı olarak çıkan () görülecektir gözlemci tarafından maviye – kaymış bir şekilde :
Relativistik olmayan sınırda, her iki Formüllerle de ( 1 ) ve ( 2 ) elde edilir.
Yoğunluk üzerinde Doppler Etkisi
Doppler etkisi de algılanan kaynak yoğunluğunu değiştirir : bu frekans küp bölü kaynak gücü Lorentz değişmez olduğu gerçeği ile kısaca ifade edilebilir [4] (Burada , " kaynak gücü " spektral yoğunluk de ' frekansı ' , yani birim katı açı başına ve birim frekansı başına iktidara eder , hertz başına steradian başına watt cinsinden ifade ; ' dalga boyu ' ' spektral yoğunluğu , küp) beşinci güç tarafından değiştirilmesi gerekir. Bu da toplam radyant yoğunluğu ( tüm frekansları üzerinden toplanmasıyla ) frekans Doppler faktörünün dördüncü güç ile çarpılır anlamına gelmektedir.
Bunun bir sonucu olarak , Planck'ın yasası frekans orantılı bir spektral yoğunluğuna sahip olarak kara cisim radyasyonu açıklanmaktadır (T burada kaynak sıcaklığı ve biz ' bir siyah cisim spektrumu hala) keyfi yönü ile bir Doppler kayması ( keflfe bir siyah cisim spektrumu ' ' sonucuna çizebilirsiniz ) frekans v frekansıyla aynı Doppler faktörü ile çarpılan bir sıcaklıkta .
Hızlandırılmış hareket
.png.webp)
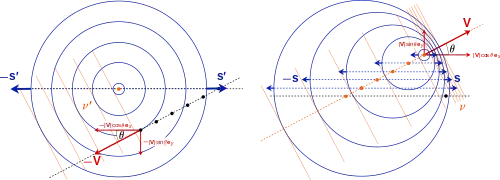
Kaynak ve alıcı hareketleri rastgele Eylemsiz incelendiğinde Genel hızlandırılmış hareketi için ya da , kaynak ve vericisinin hareket arasındaki fark dikkate alınmalıdır.
Eylemsiz gözlenen Doppler kayması :[5]
- emisyon zamanda kaynak hızı
- zamanda alıcı hızıdır
- Işık hızı vektörü
- Kaynak hız ve emisyon sırasında ışık hızı arasındaki açı
- Alıcı hız ve yansıması sırasında ışık hızı arasındaki açı
paralelse , daha sonra olur, alıcı tarafından ölçülen frekans kaynağında yayılan frekans göreli artış meydana gelir . Benzer şekilde, eğer anti-paralelse , olur, alıcı tarafından ölçülen frekans kaynaktan çıkan frekansa göre azalış meydana gelir .
Bu alıcı ve kaynak Lorentz çarpanlarının oranı ile çarpılması klasik Doppler etkisi olduğunu söyler.
Kırılma olasılığına karşı , emisyonda ışığın yönü aynı genellikle yansımada onun yönüyle aynı değildir . Kırılma meydana geldiğinde, ışığın yolunu genellikle emisyon ve yansıma noktaları arasındaki düz mesafeden sapar. Doppler etkisi emisyonda ışığın yönüne doğru yayar ve hız paralel bileşenine bağlıdır ve emilimde de ışığın yönünde alıcının hız paralel bileşeni vardır.[6] Ve bu da özel görelilik ile çelişmez.
Enine Doppler etkisi , kaynak ve alıcı eşit ve zıt hızlara sahip bir referans çerçevesinden analiz edilebilir . Böyle bir çerçevede Lorentz faktörler oranı her zaman 1 olduğu ve tüm Doppler kaymaları kökenli klasik olduğu görülmektedir. Genel olarak , gözlemlenen bir frekans kayması değişmez , ancak zaman genişlemesi ve Doppler etkisi göreceli katkıları çerçevesine bağlıdır.
Notlar
- maksimum hızı hakkında daha fazla tartışma için Makalesine bakın [ [ ] yerçekimi Hız ] fiziksel fenomenlerin etkileşim.
Bibliyografya
- Einstein, Albert (1905). "Zur Elektrodynamik bewegter Körper". Annalen der Physik (Almanca). 322 (10). ss. 891-921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004. English translation: ‘On the Electrodynamics of Moving Bodies’25 Nisan 2011 tarihinde Wayback Machine sitesinde arşivlendi.
- A. Einstein (1907), "Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips", Annalen der Physik SER.4, no.23
- J. Jackson, Classical Electrodynamics, 3rd ed. (Wiley, New York, 1999).
- Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (Şubat 1977). The Feynman Lectures on Physics: Volume 1. Reading, Massachusetts: Addison-Wesley. ss. 34-7 f. ISBN 9780201021165. LCCN 2010938208.
Dış bağlantılar
- M Moriconi, 2006, Special theory of relativity through the Doppler effect
- Warp Special Relativity Simulator12 Aralık 2007 tarihinde Wayback Machine sitesinde arşivlendi. Computer program demonstrating the relativistic Doppler effect.
- The Doppler Effect at MathPages
Kaynakça
- Landau, L.D.; Lifshitz, E.M. (2005). The Classical Theory of Fields. Course of Theoretical Physics: Volume 2. Trans. Morton Hamermesh (Fourth revised English bas.). Elsevier Butterworth-Heinemann. ss. 1-3. ISBN 9780750627689.
- Ives, H. E.; Stilwell, G. R. (1938). "An experimental study of the rate of a moving atomic clock". Journal of the Optical Society of America. 28 (7). s. 215. Bibcode:1938JOSA...28..215I. doi:10.1364/JOSA.28.000215.
- Hasselkamp, D.; E. Mondry; A. Scharmann (1 Haziran 1979). "Direct observation of the transversal Doppler-shift". Zeitschrift für Physik A. 289 (2). ss. 151-155. Bibcode:1979ZPhyA.289..151H. doi:10.1007/BF01435932.
- Johnson, Montgomery H.; Teller, Edward (Şubat 1982). "Intensity changes in the Doppler effect". Proc. Natl. Acad. Sci. USA. 79 (4). s. 1340. Bibcode:1982PNAS...79.1340J. doi:10.1073/pnas.79.4.1340.
- Kevin S Brown. "Doppler Shift for Sound and Light". Mathpages. ss. 121-129. Erişim tarihi: 6 Ağustos 2015.
- Chao, Mayer (1971). "An Additional Effect of Tropospheric Refraction on the Radio Tracking of Near-Earth Spacecraft at Low Elevation Angles" (PDF). 3 Mart 2013 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 6 Ağustos 2015.
