Kuantum kütleçekim

Kuantum kütleçekim kuramsal fiziğin bir dalı olup doğanın temel kuvvetlerinden üçünü (elektromanyetizm ve etkileşimleri) tanımlayan kuantum mekaniği ile dördüncü temel kuvveti kütleçekimin kuramı olan genel göreliliğini birleştireceği düşünülen bir kuramdır.

Dört temel kuvveti birleştirmede karşılaşılan güçlüklerin çoğu evrenin işleyişi hakkındaki bu teorilerin birbirlerinden tümüyle farklı kabullerinden doğmaktadır. Örneğin kuantum mekaniğinde mutlak bir zaman varken genel görelilikte her gözlemcinin kendisine göre ayrı birer zaman mefhumu vardır. Kuantum kütleçekim yolunda karşılaşılan bir başka güçlük de deneysel veri eksikliğidir. Kuantum kütleçekimini test etmek için gerekli enerji ve koşullar (Planck ölçeği) hal-i hazırdaki teknolojimiz için ulaşılamaz durumdadır. Şimdilik hiçbir deneysel gözlem tarzına ilişkin bir veri sağlayabilmiş değildir. Bu duruma tezat olabilecek bir durum ateşten set paradoksunda karşılaşılmıştır. O tartışmalarda kuantum kütleçekim etkilerinin daha önce öngörülemeyen büyük bir ölçekte, kara deliğin olay ufku ölçeğinde, tezahür ettiği iddia edilmektedir.

Kuantum kütleçekim teorileri bildiğimiz uzay-zaman kavramlarının ortadan kalktığı kuantum dalgalanmalarını öngörür. Bu dalgalanmalar uzay-zamanın Planck ölçeğinde adeta köpük gibi kabardığını ifade eder.

Kütleçekiminin şimdiki hali, Albert Einstein'ın genel görelilik teorisi baz alınarak oluşturulmuştur. Genel görelilik teorisi de, klasik fiziğin yapısına göre şekillendirilmiştir. Diğer bir taraftansa, kütleçekimsel olmayan kuvvetler, kuantum mekaniği taban alınarak açıklanabilir. Kuantum mekaniği, fiziksel fenomenleri tamamen farklı bir formda ele alır ve olasılık tabanlı çalışır. Kütleçekiminin kuantum mekaniği ile açıklanması gerekliliği, iki klasik sistemin, tek bir kuantum sistemine dönüştürmesi sorununu ortaya çıkarttı.

Genel göreliliği, kuantum mekaniği yasaları ile birleştirmek için, kuantum kütleçekim teorisine ihtiyacımız olmasına rağmen, kuantum alan yönergeleri, yerçekimi kuvveti ile bağdaştırılırken çeşitli problemler ortaya çıkmaktadır. Teknik bir noktadan bakılınca, teori uygulandığı noktada çalıştığı şeyi tekrar normalleştiremiyor ve bu da teorinin anlamlı fiziksel tahminler yapmasını engelliyor. Sonuç olarak, kuramcılar kuantum kütleçekim için daha radikal yaklaşımlar oluşturdular bunlardan en popülerleri sicim kuramı ve ilmek kuantum kütleçekimi. Son gelişmelerden Casual Fermion Systems adı verilen teori , kuantum mekaniği , genel görelilik ve kuantum alan teorisini kısıtlayarak oluşturuldu.

Kuantum kütleçekiminin tek amacı kütleçekimsel alanların kuantum davranışlarını açıklamaktır ve bu amaç geri kalan bütün etkileşimleri tek bir matematiksel çatı altına toplaya çalışmak ile karıştırılmamalıdır. Yerçekiminin mevcut anlayışındaki herhangi bir gelişim, bütün etkileşimlerin birleştirilmesi için biraz daha çalışmaya ihtiyacımız olduğunu gösteriyor. Kuantum kütleçekim çalışması ise, içinde pek çok branş barındıran ve birleştirilme olayına çok farklı yaklaşımları olan bir çalışma alanı. Sicim teorisi gibi, yerçekimini diğer temel kuvetlerle açıklamaya çalışan kuantum kütleçekim teorilerine rağmen, loop kuantum kütleçekim gibi diğerleri ise, kuantum yerçekimini diğer kuvvetlerden ayrı tutarken, kuantlar haline getirmeye çalışır. Kuantum kütleçekim teorisi ya da diğer bir deyişle büyük birleşik kuram olarak bilinen bu olay, bazen de "her şeyin teorisi" olarak da bilinir.

Kuantum kütleçekiminin bir diğer zorluğu ise, bu kütleçekimsel etkilerin yalnızca Plank ölçeğine yakın değerlerde görünmesinin beklenmesidir. Bu ölçek, yüksek enerjili parçacık ivmelendiricilerin sınırlarında erişilebilir, ufak sınırlarda bir ölçektir. Sonuç olarak, her ne kadar kuantum kütleçekim genel anlamda teorik bir girişim gibi görünse de, hala kuantum kütleçekim etkilerinin bazı deneylerde görüntülenebileceğine dair spekülasyonlar vardır.

Genel bakış
Diagram showing where quantum gravity sits in the hierarchy of physics theories

Bu teorileri bütün enerji düzeylerinde kavramanın zorluk çıkartan tarafı genelde bu teorilerin evrenin nasıl işlediğine dair yaptıkları varsayımlardan kaynaklanır. Kuantum alan teorisi, özel göreliliğin düz uzay zamana gömülmüş parçacık alanlarına dayanır. Genel görelilik ise, yerçekimini uzay zamanla bükülen ve kütleye göre değişen bir kavram olarak modellemiştir. Tarihsel olarak, renormalizasyon problemi olarak bilinen yol iki durumu ( örneğin yerçekimini diğer parçacık alanları gibi düşünmek) kolayca birleştirmek için en bariz yoldur. Renormalizasyon eski anlayışa göre, kütleçekimsel parçacıklar birbirlerini etkiler ve bu etkileşimlerin birbiriyle toplamı matematiksel olarak kolayca hesaplanamayacak kadar, pek çok sonsuz sonucu oluşturacaktır. Bu durum, kuantum elektrodinamiği ile çelişen bir durumdu. Bulunan bu seriler hala bir noktada toplanamadı, bu etkileşimler bazen sonsuz sayıda sonuçlar yaratıyor, ancak aralarında yeterli sayıda renormalizasyon aracılığı ile çıkartılabilenler var.

Etkili alan teorileri

Kuantum kütleçekimi, etkili bir alan teorisi olarak görülebilir. Etkili kuantum alan teorileri yüksek enerji kesintileri ile gelir. Bu bizim, teorinin doğanın işleyişini güzelce açıklamasını beklememizden daha ötesinde. Böylece sonsuzluklar, bu yüksek enerji kesikliklerine bağlı olarak çok geniş fakat sonlu niceliklere dönüşür ve temel kesintileri çok yakınında gerçekleşen olaylara karşılık verebilecek hale gelirler. Bu nicelikler sonsuz sayıda bağlanma katsayılarına dönüşebilirler ve enerjileri teorideki kesilme enerjisinin altında kalır. Aynı mantık, kuantum kütleçekimindeki düşük enerjili piyonlar için de bayağı başarılı bir şekilde çalışır. Hatta, kütleçekim serpintileri ve Newton'ın yerçekim kanunu dahi belirgin olarak tahmin edilmiştir. (neredeyse bizim ölçemeyeceğimiz kadar sonsuz küçüklükte olmalarına rağmen). Aslında yerçekimi pek çok yönden bir kuantum alan teorisi olarak Standart Model'den daha iyi. Çünkü şimdiye kadar Plank Skalasının her ölçüsünde geçerli gibi görünüyor.

Kuantum mekaniği ve kütleçekim bir yandan cidden tutarlı yüksek enerjiler olduğunu doğrularken, temel enerji kesintilerinini altında ya da yakınında kaldığımızda, yeni bir doğa modellemesi gerekli oluyor. Özellikle kuantum mekaniğini ve kütleçekimini kombinlemek, yüksek enerjilerde zor bir hal alıyor ve bu nedenle belki de yeni bir modellemeye ihtiyaç duyuyordur.

En yüksek enerji skalaları için kuantum kütleçekim

Kuantum kütleçekim teorisini türetme fikri ile ilgili genel tutum, en yüksek enerji seviyelerinde bile geçerli olan , basit, elegant simetriler ve öbür ip uçları üzerinde çalışmaya yatkın ve bunları kombinlemek için yollar gösterebilecek bir şey arayışıdır. Bu tutumla ilgili sorunlardan biri kuatum kütleçekiminin dahi basit, elegant ve tek bir teori olup olamayacağı sorusudur. Çünkü özel görelilik ve ivme ve kütleçekim birleşmezliğindeki ikilem ya da genel görelilik ve uzay zamanın bükülmesi gibi çıkmazları olabilirdi.

Bu tarz teoriler , yüksek enerjilerin ve evrenin çok küçük boyutlarının kombinlenmesi de dahil, evrenin merkezi veya karadeliklerin davranışları gibi problemleri anlamak için gereklidir.

Kuantum mekaniği ve genel görelilik
Gravity Probe B (GP-B) has measured spacetime curvature near Earth to test related models in application of Einstein's general theory of relativity.

graviton

Günümüzde, teorik fiziğin en kökü problemlerinden biri, yerçekimini açıklayan, yıldızlar ve gezegenler gibi büyük ölçekli cisimlerin uygulamasını yapan genel görelilik ile atomik boyuttaki temel kuvvetleri açıklayan kuantum mekaniğinin kaynaştırılmasıdır. Bu problem uygun bir bağlama sokulmalıdır. Özellikle, gene kültürün kuantum mekaniği ve genel göreliliğin uyumsuzluk içinde olduğu düşüncesine rağmen, kuantum mekaniğinin teorik spini iki kütlesiz parçacığın (gravitonlar) etkileşimi ile oluştuğu ve genel göreliliği takip eder olduğu gerçeğini rahatlıkla kanıtlayabilir

Gravitonların varlığa dair somut bir kanıt yokken, maddenin kuantlaşmış teorileri, bu parçacıkların varlığını gerekli kılmaktadır. Bu teoriyi, Messenger parçacıkları denen ve temel kuvvetlerden yerçekimi hariç hepsinde bulunan bu parçacığın gözlemi, araştırmacıları en azından bir taneciğin var olması gerektiği inancına sevk eden şey oldu. Böylece, bu varsayımsal parçacıklara, graviton unvanı verilmiş oldu. Elektromanyetik alandaki fotonlar gibi, bu parçacık da kuvvet parçacığı sınıfına konulmuş oldu. 1970'lerde ve sonrasında varsayılmış pek çok fiziksel kavram, gravitonların varlığına dayandırılarak hesaplandı, oluşturuldu. Bu teorilerden bazıları, sicim kuramı, süper sicim kuramı, M-teorisi ve ilmek kuantum kütleçekimidir. Gravitonların tespiti, bu nedenle kuantum mekaniğinde ve görelilik teorilerindeki pek çok araştırma alanına öncülük etmiştir.

dilaton

Dilaton, ilk olarak Kaluza-Klein teorisinde görülmüştür. Bu teori yerçekiminin ve elektromanyetizmanın beş boyutta birleştirilmesini anlatır. Genellikle, sicim kuramında ortaya çıkar. Fakat son zamanlarda, Roman Jackiw'in alan teorik alan yaklaşımıyla, düşük boyutlardaki objeler için de , merkezde yer alır bir hale gelmiştir. Tamamen analitik çözümleri olan enerji yükselmeleri ile metrik N-obje sistemi genel görelilikteki anlaşılmazlığı kanıtlamıştır. Problemi basitleştirirsek, boyut slayısı (1+1) e kadar indirgenmiştir. Yani bir uzaysal bir de zamansal boyut olarak. Bu model problem, R=T theory olarak da bilinir. G=T teorisinin tersidir. Diferansiyel geometriden türetilen, dilaton a hükmeden alan eşitliklerinde de bulundu. Aynı zamanda Schrödinger eşitlikleri ve son zamanlarda kuantizasyona da bağlı hale gelmiştir.

Bu yüzden, eğer birisi yerçekimini, kuantizasyonu ve hatta elektromenyetik alan etkileşimlerini kombinleyen bir teoriye sahipse, bu teori temel fiziğin teorisi için gelecek vadeden bir teori olacaktır. Hatta, bu "icadın" genel görelilik ve kuantum mekaniği arasında çoktandır var olan ancak hala keşfedilememiş doğal ilişkiyi ortaya çıkartacağını söylemekte de yarar var. Ancak bu teori (2+1) ve (3+1) boyut genellemesinin eksikliğini yaşayacaktır. Prensip olarak, alan eşitlikleri bu tarz genellemelerin sorumluluğunu alır ve Newton Mekaniğindeki " d " kadar boyut kısıtlamasının doğruluğunu gösterir ancak bu sadece dilaton hesaplamalara dahil edildiğinde gerçekleşir. Dahası, dilatonun (3+1) boyutlarında hükmedilmesi gerektiğini anlatan alan teorilerinin genelleştirilmesi tamamen netleştirilmemiştir. Dilatonların (3+1) boyutlarında çoğalabildiği gerçeği, gravitonların ve dilatonların gerçek dünyada da var olması gerektiğini kanıtlamaktadır. Mamafih, dilatonun varlığı, garavitonların varlığından çok daha anlaşılmazdır. Fakat, yerçekimini, elektromanyetik ve kuantum etkilerinin kombinlenebileceğine dair yaklaşımlar basitleştirildiklerinde , bu birleşim teorinin doğruluğunun kanıtlanabileceği bir potansiyele sahip olacak. Hem kozmolojik olarak hem de deneysel olarak.

Kütleçekiminin yeniden normalleştirlememesi

Genel görelilik, elektromanyetizma gibi, klasik bir alan teorisidir. Dolayısıyla, kuantum alan teorisinde, kütleçekimsel kuvvetlerin de bir karşılığının olması beklenebilir.

Ancak kütleçekim, kaygı verici bir şekilde renormalizasyona uygun değildir. Kuantum alan teorisinin iyi tanımlanmış olması anlaşılabilirliği açısından önemlidir. Asimtotik olarak özgür ya da güvenilir olmalıdır. Pek çok sonlu seçenek tarafından karakterize edilebilmeli ve deneysel olarak kurgulanabilmelidir. Örneğin kuantum elektrodinamiğinde bu tarz parametreler yük ve elektronun kütlesidir ve belirli enerji skalalarında ölçülebilirdirler.

Fakat diğer taraftan, teoride, kütleçekimini kuantize edebilmek için pk çok sozsuz ve bağımsız parametreler ( katsayılar ) , teoriyi tanımlayabilmek için gereklidir. Bu parametrelerden verilenler arasında, sozsuz deneylerle her parametrenin değerine ulaşmak fikri ile ilgili, herhangi anlamlı bir fiziksel teoriye sahip değiliz.

  • Düşük enerjilerde, renormalizasyon gruplarının bize söylediği mantık, sonsuz pek çok parametre seçeneğine rağmen, kuantum kütleçekimi, Einstein'ın genel görelilik teorisi daha basit bir hale dönüştürür.
  •  Diğer bir yandan, kuantum etkilerinin yetkiyi devraldığı düşük enerjileri detaylıca inceleyebilirsek, her bir sonsuz ve bilinmeyen parametreler bir etkiye sahip olacaktır ve biz bunların hepsini tahmin edemeyeceğizdir.

Eğer kuantum kütleçekim teorisini, etkli bir alan teorisi kabul edecek olursak, bu problemde bir yol vardır.

Bu yol, kuantum kütleçekim teorisinin mantığını çok köklü bir prensiple açıklar ( bu prensip bütün enerji seviyelerinde gözlemlenebilr ) ve bu prensip sonsuz sayıda bilinmeyen pen çok parametreyi, sonlu pek çok parametreye, ölçülebilir bir hale çevirir.

  •  Bu ihtimallerden biri normal Perturbation Teorisinin renormalize edilemeyişi ve renormalize edilebileceğine dair olan güvensizlik ve UV sabitlenmiş noktanın kütleçekimde gerçekten var olmasıdır.
  • Diğer olasılık ise, hala bulunmamış yeni simetri prensipleri olmasıdır. Bu prensipler sonlu bir set hazırlayabilecek halde olmalıdır. Bu çatı, sicim teorisi altında toplanabilir. Bu teoride, bütün varoluşlar sicimin altında kendileriyle yeni simetriler oluşturabilirler.

Etkili bir alan teorisi olarak kuantum kütleçekim

Etkili bir alan teorisinde, renormalize edilemeyen teorideki sonsuz parametre setlerinin tamamı olmasa da bir kısmının yüksek enerji sklalarında bastırılmıştır. Bu nedenle, düşük enerji seviyelerinde yok sayılabilirler. Düşük enerji rejimlerinde bu model öngörülebilir bir kuantum alan teorisi olarak düşünülebilir. Dahası, pek çok teorikçi Standart modelin etkili bir alan teorisi olarak düşünülmesi gerektiğine inanıyor.

Son çalışmalar, genel görelilik teorisinin etkili bir alan teorisi olarak değerlendirildiğinde, kuantum kütleçekim hakkında en azından düşük enerji skalalarında tahminlerde bulunabileceğini gösterdi. İlk dereceden kuantum mekaniği hesaplamaları, klasik Newton Mekaniğinin iki kütle arasındaki yerçekim potansiyelini doğruladığı örneği, çok iyi bilinen bir gerçektir.

Uzayzaman arka plan bağımlılığı

Genel göreliliğin en temel derslerinden biri, belirli bir uzayzaman arka planının olmayışıdır. Newton Mekaniği ve genel görelilikte de bulunduğu gibi, uzayzaman geometrisi dinamiktir. Her ne kadar prensipte kavramak zor olmasa da, genel görelilik hakkındaki en zor fikirdir. Sonuçları da, klasik seviyede bile kesinleşmemiştir. Daha geniş bakılırsa, genel görelilik bir ilişkisel teori olarak görülebilirken, uzayzamandaki değişik olaylar arasında güvenilebilir bağlantılar oluşturur..

Diğer bir yandan, kuantum mekaniği başlangıcı belirlenmiş bir arka plana (dinamik olmayan) bağlıdır. Kuantum mekaniği durumunda, dinamik olmayan Newton Mekaniği gibi düşünülebilir. Gerçekçi kuantum alan teorisinde , klasik alan teorisinde olduğu gibi, Minkowski Uzayzaman teorisi, belirlenmiş arka planlı bir teoridir.

Sicim teorisi
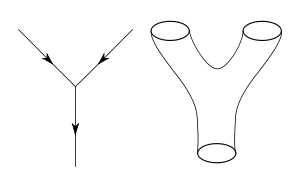
Interaction in the subatomic world: world lines of point-like particles in the Standard Model or a world sheet swept up by closed strings in string theory

Sicim teorisi, kuantum alan teorisinin genellemesi olarak görülebilir. Bu teoride, sicim benzeri objeler fikslenmiş bir uzayzaman arka planına sahiptirler. Ki gözlemlenebilen yakın sicimler arasındaki etkileşimler, uzay zamanın dinamik kısımlarında meydana gelmiştir. Her ne kadar sicim teorisinin kökeni kuantum kütleçekime değil de kuark sınırlandırmasına dayansa da, sicim spekturumlarının gravitonları barındırdığı sonunda keşfedildi. Bu yoğunlaştırma, sicimlerin belirli titreşim mollerinde , orijinal arkaplnda değişime gidilmesine neden oldu. Bu anlamda, Sicim perturbasyon teorisi, pertubasyon teorisinden beklenen şekilde pek çok asimptotik dayanaklarının olduğunu göstermiş oldu.

Arka plandan bağımsız teoriler

Loop Kuantum Kütleçekimi, arka plandan bağımsız kuantum teorilerinin formuluzasyonundan meydana gelen bir teoridir.

Topolojik kuantum alan teorisi arka plandan bağmsız kuantum teorileri tarafından doğrulanmış bir kuantum alan teorisidir. Fakat herhangi bir yerel bağımsızlık derecesi yoktur. Yalnızca, sonsuz sayıda global bağımsızlıklara sahiptir. Kütleçekimini (3+1) lik bir boyutta tanımlamak yetersiz olacağından, local dereceleri genel göreliliğe göre bağımsız olan sisteme dayandırılmıştır. (2+1) boyutlarında ise, kütleçekim, topoğrafik alan teorisidir. Ayrıca, pek çok farklı yaklaşımla, başarılı bir şekilde kuantize edilebildiği görülmüştür.

Kısmen klasik kuantum kütleçekim

Bükülmüş arka planlardaki kuantum alan teorisi ( Minkowskian olmayan ) tam bir kuantum kütleçekim teorisi olmasa dai önceki sonuçlarla umut vadedecek bir şekilde örtüşen yanları vardır. Yirminci yüzyılın ilk yıllarındaki kuantum elektrodinamiğinin gelişiminde önemli bir yoldur. Bükülmüş arka planlardaki kuantum alan teorilerinin kara deliklerden salınan radyasyonlarla ilgili de pek çok tahmini vardır.

Unruh Etkisi olarak da bilinen olayda, bazı ivmeli düzlemler yer alır. Ancak sabit olanlar, bükülmüş arka plan düşüncesinde herhangi bir zorluğa neden olmaz. Vakum seviyeleri düşüktür. Bükülmüş uzay zaman arka planında kuantum alan teorisi başlığına bakarak daha ayrıntılı bilgi edinebilirsiniz.

Çekişme noktaları

Kuantum Mekaniği ile Genel görelilik arasında başka çekişme noktaları da vardır.

  • Birincisi, klasik genel görelilik tekilliklerde geçersizdir. Kuantum mekaniği ise genel göreliliğin komşu tekilliklerinde güvenilmez bir hale gelir. (fakat, hiç kimse klasik genel göreliliğin, ilk başta tekilliklere uygulanabileceğine ihtimal vermiyordu)
  • İkincisi, bir parçacığın kütleçekimsel alanının nasıl belirleneceği kesin değildi. Çünkü, kuantum mekaniğinin Heisenberg belirsizlik ilkesi, bir parçacığın aynı anda hem konumunun hem de hızının belirlenemeyeeğini söylüyordu. Bu noktalar için çözüm, genel göreliliğin daha iyi anlaşılmasından geçiyor olabilirdi
  •  Son olarak, kuantum kütleçekiminde zaman problemi vardır. Kuantum mekaniğinde ve genel görelilikte zaman iki farklı anlama gelir. Bu nedenle bu iki teorinin kombinlenmesinde , zaman karmaşası sıkıntı yaratmaktadır.

Aday teoriler

Pek çok gelecek vadeden kuantum kütleçekim teorisi vardır. Son zamanlarda ise, hala tamamlanmamış ve kesin olmayan kuantum kütleçekim teorisi ve konseptsel ve büyük problemlerin üstesinden gelmesi gereken modellemelere ihtiyaç duyuyoruz. Bu teoriler aynı zamanda ortak problemlerle de yüzleşiyor. Kuantum kütleçekim öngörülerini deneylere tabi tutmak mümkün olmasa da, ilerleyen zamanlarda kozmolojik datalar ve gözlemler sayesinde, parçacık fiziğinde deney yapabilmeyi umuyoruz.

Sicim teorisi
Projection of a Calabi–Yau manifold, one of the ways of compactifying the extra dimensions posited by string theory

Diğer sıradan kuantum alan teoriler için önerilen bir diğer başlama noktası ise, diğer üç temel kuvveti doğruca açıklayabilen yeni başlayanlar için parçacık fiziğindeki Standart Model'in başarılı bir şekilde açıklanabilmesidir. Fakat bu, düşük enerjilerdeki kütleçekimsel ve etkili kuantum teorileri kabul edilmesine yardım ederken, kütleçekim yüksek enerjilerde sıkıntılı bir hal almaya başlamıştır. Kuantum elektrodinemiği, renormalizasyon tekniği olarak bilinen integralle yüksek enerji seviyelerini türetmek gibi diğer sıradan alan teorileri için çalışırken, kütleçekim renormalize edilemez bir hale gelmektedir. 

Kuantum alan teorisinin neden olduğu sınırlamaların üstesinden gelmek için bir başka yolsa, klasik noktasal parçacık fikrinden geçer. Bu teoriyle beraber bir boyutsal sicim teorisi de kullanılmalıdır. Son deneylerde ulaşılan yüksek enerjilerde, bu sicimler noktasal parçacıklardan ayrılamaz bir haldedir ancak, salınımın farklı modelleri ve aynı şekildeki temel sicimler diğer yüklerden farklı olarak görünürler. Bu method ile , sicim teorisi parçacıklar arasındaki etkileşimlere birleştirilmemiş bir açıklama getirir. Gravitonu her zaman karşılayacak, bir model sunmada başarılırdır. Messenger parçacıkları ise, alışılmamış nicelikler 6 boyutlu uzay zaman gibi durumlarda ancak geçerlilik görebilirler.

İkinci süpersicim devrimi denen, hem sicim teorisinin hem de genel göreliliğin birleşimi zannedilen ve süpergravity olarak bilinen süpersimetrinin, M-teorisi olarak da bilnen 11 boyutlu teorinin bir kısmına dayandırılarak, açıklanabileceği düşnülüyordu. Günümüz anlayışı ile , sicim teorisinin 10^500 gibi rakamlarda olduğu kabul edildi. Bütün bu değişik çözümler ve problemler, çok ciddi bir meydan okuma olarak hale geçerliliğini koruyor.

Loop kuantum kütleçekim
Simple spin network of the type used in loop quantum gravity

Loop kuantum kütleçekim genel göreliliği uzayzaman içgüdüsünde, kuantum cismi olarak değerlendirilebileceğini iddia eder. İkinci fikri ise, kuantumun açıklığının parçacık gibib olan objelerin diğer alan teorilerindeki davranışlarının açıklanmasına yardımcı olacağı görüşüdür.

Loop kuantum kütleçekiminin en önemli sonucu, Plank aralığında uzayın tanecikli bir iskelete sahip olmasından türetilmiştir. Elektromanyetik açıdan bakılınca, kuantum operatörleri her frekanstaki enerjinin gizli olmayan bir spekturumu bulunduğunu söyler. Bu nedenle, her her enerji frekansı kuantize edilmiştir. Bu kuantalara da foton adı verilir. Kütleçekim açısından bakılırsa, alan ve hacmi temsil eden operatörler, yüzey ve uzay gibi gizli olmayan spektrumlara sahiplerdir. Bu nedenle herhangi bir porsiyonun alan ve hacimleri de kuantize edilmiştir. Bunlar uzayın kuantalarıdır. Bu da uzay zamanın başlangıç için plank skalasında tanecikli olduğu fikriyle takip edilir.

Uzayzamanın kuantum boyutları spin network adı verilen bir matematiksel tabanla açıklanır. Spin Networkler ilk başta Roger Penrose tarafından açıklanmıştır daha sonra da Carlo Rovell, ve Lee Smolin tarafından doğal formuna türevlenmiştirler. Spin networkleri uzayda bir alanın kuantum seviyesini belirtmez. Direkt olarak uzayzamanın kuantum seviyesini belirtir.

Teori, genel görelilik teorisinin olan ve Ashtekar değişkenleri olarak da bilinen teorinin reformalizasyonunu taban alır. Ashtekar değişkenleri, geometrik kütleçekimini elektrik ve manyetik alanların matematiksel analoglarıyla temsil eder. Kuantum teorisinde, uzay, spin networkleri denilen networklerle temsil edilir.

Teorinin bugünkü dinamikleri ise yapısal olarak pek çok değişkenlik gösterir. Bu versiyonlardan biri, genel göreliliğin kanonikal kuantizesi ile başlar. Schrödinger eşitliklerinin analogları bir Wheeler-DeWitt eşitliğidir ve bu eşitlik teori ile açıklanabilmektedir. Eş değişkende veya spinfoam denen bir topolojik modellemede, teorinin formülüzasyonuyla, kuantum dinamikleri, uzayzamanın ayrık versiyonlarının toplamı olarak elde edilir bunlara da spinfoam denilir. Spin networklerin geçmişleri, bu spinfoamlar tarafından temsil edilir.

Diğer yaklaşımlar

Kuantum kütleçekim ile ilgili pek çok sayıda farklı yaklaşım bulunmaktadır. Bu yaklaşımlar, genel göreliliğin ve kuantum teorisinde değiştirilmediği kabul edilen hangi özelliğe bağlı olduklarına bakılarak farklılık gösterir. Bazı örnekler ;

  •  Akustuik metrik ve diğer kütleçekim analog modelleri
  •  Kuantum kütleçekiminde asimptotik güvenilirlik
    • Euclidean Kuantum Kütleçekimi
  • Nedensel Dinamik Üçgenleştirme
    • Nedensel fermiyon sistemleri, kuantum mekaniğini, genel göreliliği ve kuantum alan teorisinin sınırlandırılarak verilmesi. 
    • Nedensel setler
    • Kovaryant Feynman yolunda integerasyon
    • Grup alan teorisi
    • Wheeler-DeWitt Eşitlikleri
  •  Geometrodinamikler
    • Hořava–Lifshitz Kütleçekim
    • MacDowell–Mansouri Aksiyonu
  • Değiştirilebilen Geometri
  •  İntegral yolu tabanlı Kuantum Kozmolojisi modelleri
    • Regge Calcülüsü
  • Şekil Dinamikleri
  • String-nets giving rise to gapless helicity ±2 excitations with no other gapless excitations[1]
    • Süperakışkanlar Vakum Teorisi
  • Supergravity
    • Twistor Teorisi
    • Kanonik Kuantum Kütleçekimi
    • E8 Teorisi
    • Kuantum Holonomi Teorisi

Weinberg–Witten theorem

Kuantum alan teorisinde, Weinber-Witten teorisi, kütleçekim ve yeni kütleçekim algısının karışımından oluşan bir takım teoriler barındırır. Fakat, son gelişmeler, lokalleşme eğer tek yaklaşımsa ve holografik prensip doğruysa, Weinberg-Witten teoreminin gerçerli olamayacağını destekler nitelikte.

Deneysel testler

Yukarıda daha önce de belirttiğimiz gibi, kuantum kütleçekimsel etkiler ziyadesi ile zayıf ve bu nedenle teste tabii tutulması zor kuvvetlerdir. Bu nedenle, kuantum kütleçekimini test etme ihtimali, 1990'lardan önce çok da cezbedici bir alan değildi. Fakat, geçtiğimiz zamanda fizikçiler, kuantum alan teorisinin etkilerinin teoriyi geliştirebileceğe güvenmeye başladı. Teorik gelişimler yavaş olduğundan, fenomenolojik kuantum kütleçekim alanı, bu deneylerin yapılabilme ihtimali üzerinde çalışıyor ve gittikçe dikkat çekmeye devam ediyor.

Kuantum kütleçekim fenomenoloji tarafından açık ara olasılıklar, Lorentz değişmezlikleri de dahil olarak, takip ediliyor . Kuantum kütleçekiminin parmak izlerinin kozmik arka plan ışımasında da yer aldığı düşünülüyor.

BICEP2 deneyi, ilk çağlardaki B-Mod Polarizasyonun kütleçekimsel dalgalardan, evrenin ilk yaşlarında oluştuğunu düşünüyordu. Eğer doğru ise, bu dalgalar kütleçekiminde varolan dalgalanmaların ta kendisiydi. Kozmolog Ken Olum ( Tufts Üniversitesi) : " Bence kütleçekiminin kuantize olabildiğine dair sahip olduğumuz tek gözlem budur, ve muhtemelen sahip olabileceğimiz tek kanıt da bu olacak" demiştir.

Kaynakça
  1. Wen 2006
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.