Kuantum tünelleme

Kuantum tüneli, parçacığın bariyer boyunca olan kuantum mekaniğini ifade eder. Bu, Güneş gibi yıldızlar dizisinde meydana gelen nükleer birleşmeler gibi birçok fiziksel olayda önemli bir rol oynar. Tünel diyotu, kuantum bilgisayarı ve taramalı tünelleme mikroskobu gibi modern araçlarda önemli uygulamaları vardır. Fiziksel olay olarak etkisi ve kabul görülürlüğü 20. yüzyılın başlarında ve ortalarına doğru geldiği tahmin ediliyor.

Tünelleme sıklıkla Heisenberg belirsizlik ilkesi ve maddenin dalga parçacık ikiliği kullanılarak açıklanır. Saf kuantum mekanik kavramlar olayın merkezindedir bu yüzden kuantum tüneli kuantum mekaniğinin yeni sonuçlarından biridir.

Tarih

Kuantum tüneli 1896 da Henri Becquerel tarafından keşfedilen radyoaktivite çalışmalarıyla geliştirilmiştir. Radyoaktivitenin ileriki çalışmaları 1903 yılında Nobel Fizik Ödülü'nü alan Marie Curie ve Pierre Curie tarafından incelenmiştir. Ernest Rutherford ve Egon Schweidler, daha sonra Friedrich Kohlrausch tarafından doğrulanmış olan doğası hakkında çalışmıştır. Yarı ömür fikri onların çalışmaları tarafından ortaya konulmuştur. Friedrich Hund, 1927'de çift kuyu potansiyelinin zemin durumunu incelediği zaman tünelin ilk farkına varandır. Matematikte ilk uygulaması 1928'de George Gamow, Ranold Gurney ve Edward Condon tarafından yapılan alfa bozunumu olmuştur. İki araştırmacı, tünelin matematiksel olasılığının direkt olarak ilişkili olduğu parçacığın yarı ömrü ve emilim enerjisinin arasındaki ilişkinin sürümünden ve nükleer potansiyeli için Schrödinger’in denklemini beklenmedik bir şekilde çözmüşlerdir.

Gamow tarafından verilen seminere katılımından sonra Max Born tünelin genelliliğinin farkına vardı. Born sadece nükleer fizikle kısıtlı olmadığını, birçok farklı sistem tarafından uygulanabilen, kuantum mekaniğinin genel bir sonucu olduğunun farkına vardı. Kısa bir süre sonra, iki grupta çekirdekteki parçacık durumlarını göz önüne aldı. Yarı iletkenler üzerindeki çalışmalar, transistörlerin geliştirilmesi ve diyotlar katılardaki elektron tünelinin varlığının kabulüne 1967 yılında yol açtı. Leo Esaki’nin çalışmaları, Ivar Giaever ve Brian Josephson’ın 1973 yılında Nobel Fizik Ödülü'nü alan süper iletken Cooper çiftlerinin tünelinin tahmin edilmesini sağladı.

Kavrama giriş

Bariyer boyunca kuantum tüneli. Tüneldeki parçacıkların enerjileri eşit fakat genlikleri giderek azalmakta.

Bariyer boyunca kuantum tüneli. Orijinde (x=0) yüksek ama sınırlı potansiyel bariyer. Önemli tünel efekti görülmektedir.

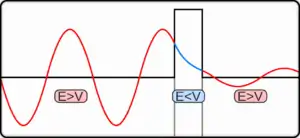
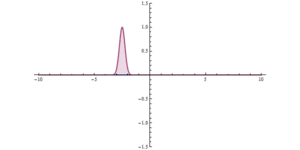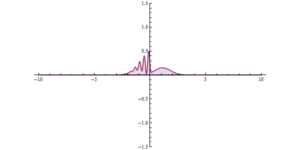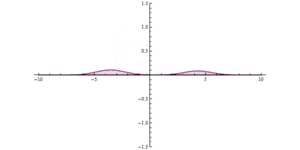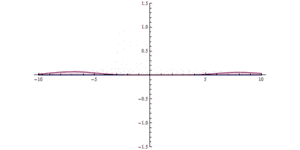
Kuantum tüneli kuantum boyutunda neler olduğunu çalışan kuantum mekaniği alanında başarısız olmaktadır. Bu süreç direkt olarak idrak edilemez fakat anlaşılması klasik mekaniğin yeterli kadar açıklanamadığı mikroskobik dünyada şekillenebilir. Olayı anlamak için potansiyel bariyerler arasında gezinmeye çalışan parçacıklar tepeden yuvarlanmaya çalışan bir topla karşılaştırılabilir. Bu senaryoda kuantum mekaniği ve klasik mekanik işleyiş bakımından birbirinden ayrılır. Klasik mekanik bariyerleri aşmak için yeterli enerjiye sahip olmayan parçacığın diğer tarafa ulaşamayacağını ön görür. Bu yüzden tepeyi aşmak için yeterli enerjisi olmayan top geri yuvarlanacaktır ya da duvarların arasından geçmek için yeterli enerjisi olmazsa geri sıçrama ya da bazı aykırı durumlarda kendini duvarın içine gömecektir. Kuantum mekaniğinde küçük bir ihtimalle de olsa bu parçacıklar- diğer tarafla tünel yapan- bariyerleri aşacaktır. Burada topu duvar veya yuvarlanılan tepeyi geçmek için ödünç alan olarak düşünebiliriz. Geri ödemesini elektronları ödünç aldığı halinden daha fazla enerjili bir şekilde yayarak yapacaktır. Kuantum mekaniğinde maddenin işleyişinden gelen bu farklılığın sebebi olarak dalga ve parçacıkların özelliklerini gösterilebilir. Bu ikilemin bir yorumunu parçacığın pozisyonunun ve momentumunun aynı anda bilenebileceğini de tanımlayan Heisenberg belirsizlik ilkesi içerir. Bu da çözüm sonsuza yaklaşırken sıfırın veya birin ihtimali ile sonucun olmayacağını söyler. Örneğin, bu konuma göre hesaplama 1 değerini alsın, diğeri, örneğin hızı sonsuz olabilir. Sonuç olarak diğer taraftaki parçacığın varlığının ihtimali sıfır olmayan bir değerdir ve bu tür parçacıklar benzer frekansla orantılı bir olasılıkla diğer tarafta gözükebilir.

Elektron dalgası potansiyel bariyerle direkt orantılıdır. Sağdaki sönük lambalar tünel elektronlarını göstermektedir.

Faz uzayı formülasyonunda kuantum mekaniği. ${\displaystyle U(x)=8e^{-0.25x^{2}}}$ potensiyel bariyeri için Wigner fonksiyonu (atomik birim). Keskin çizgiler Hamiltonian seviyesi setini göstermektedir.${\displaystyle H(x,p)=p^{2}/2+U(x)}$.

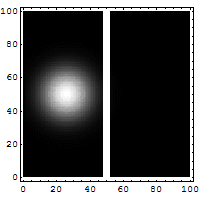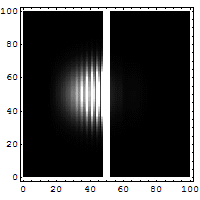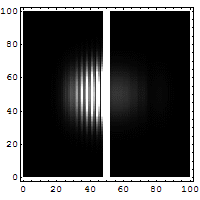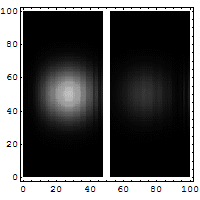
Tünelleme problemi

Parçacığın dalga fonksiyonu fiziksel sistemler hakkında bilinen her şeyi özetlemektedir. Buna göre kuantum mekaniğindeki problem sistemin dalga fonksiyonunun analizi etrafından yer bulmaktadır. Kuantum mekaniğinde Schrödinger denklemi gibi matematiksel formulasyonlar kullanılarak dalga fonksiyonları çözülebilir. Bu direkt olarak parçacığın pozisyonunun parçacığın her bir anındaki olasılığı olarak tanımlanan öz kütlesine bağlıdır. Büyük bariyerlerin sınırlarında, tünelleme olasılığı büyük ve geniş bariyerler için azalır.

Basit tünelleme bariyer modelleri için, örneğin dikdörtgen şeklindeki bariyerler, analitik sonuçları vardır. Problemler gerçek hayatta gerçek bir çözüme sahip değildirler bu yüzden bu tür problemlere yaklaşık sonuçlar verebilmek için yarı klasik metotlar geliştirilmektedir örneğin WKB yaklaşımı. İhtimaller Feynman’ın yol integral metodu ile seçmeli hassasiyetlerden sürülmektedir- hesaplamalı kaynaklar tarafından kısıtlandırılmış- bu tür hassasiyetler nadiren mühendislik uygulamasını gerektirir.

İlgili olaylar

Kuantum tünellemeyle aynı davranışlara sahip ve bu yüzden kolayca tünellemeyle tanımlanabilen birçok çeşitli olay vardır. Örnekler, klasik dalga parçacık iş birliğinin tünellenmesi, fani dalga kavramı(Maxwell denkleminin ışıkta uygulanması) ve bağımsız dala denkleminin dize dalgalar üzerinde uygulanması arasındadır. Fani dalga kavramı bu günlere kadar kuantum mekaniğinde tünelleme olarak adlandırıldı. Günümüzde ise farklı alanlarda kullanılmaktadır.

Bu modeller dikdörtgen bariyerlere benzer modellerle modellenmektedir. Bu tür durumlarda, aynı ve çok yakın sürede dala yayılması olan tek bir ulaştırma ortamı vardır. İkinci ortam ise dalgaların farklı yol izledikleri ortamdır. Bu ortam A ve ortam B’nin arasındaki ince farklılık olarak tanımlanabilir. Schrödinger’in denklemleri göz önünde bulundurularak yapılan dikdörtgen bariyerlerin analizleri A’ya giden dala çözümlerinin dalga denklemleri olarak sağlanabilir fakat gerçek çözüm B’deki üstel çözümüdür. Optikte, ortam A boşlukken ortam B camdır. Akustikte, ortam S sıvı veya gaz olabilir be ortam B katı olabilir. İki durumda da ortam A parçacığın toplam enerjisinin potansiyel enerjisinden büyük olduğu alandır ve ortam B potansiyel bariyerdir. Bunlar iki yönde de giren ve çıkış yapan dalgalara sahiptir. Birçok ortam ve bariyer olabilir ve bariyerler farklı olmak zorunda değillerdir, yaklaşımlar bu durumda kullanılabilir.

Uygulamaları

Tünelleme, 1,3 nm veya daha küçük incelikteki bariyerlerle meydana gelir. Fakat bu önemli önemli mikroskobik fiziksel olaylardır. Örneğin, tünelleme çok büyük ölçekli elektronik entegrasyonda bir akım kaynağının sızıntısıdır ve güç boşaltma, ısınma efektindeki örneğin, telefon teknolojisi ve yüksek hız gibi önemli sonuçları vardır. Bu bilgisayar çipinin nasıl küçük olabileceğinin en düşük sınırlı göstergesi olarak düşünülebilir.

Radyoaktif bozunma

Radyoaktif bozunma parçacıkların ve kararlı ürün oluşturmak için atomun kararsız çekirdeklerinden gelen enerjinin emilmesinin bir sürecidir. Bu olay parçacığın çekirdeğin tünellenmesiyle yapılır.(çekirdeğin içindeki elektron tünellemesi elektron yakalamasıdır.) Bu ilk yaklaşıma izin veren kuantum tünellemesinin ilk uygulamasıdır.

Anlık DNA mutasyonu

DNA’nın anlık mutasyonu, proton tünellemesi olarak tanımlanan kuantum mekaniğinde tek protonun yer değiştirmesinden sonra normal DNA nın kopyalanmasıyla meydana gelir. Hidrojen bağları DNA nın normal baz çiftlerine katılır. Potansiyel enerji bariyerleri tarafından ayrıştırılmış hidrojen bağları çift kuyu potansiyellerinde görülür.

Çift kuyu potansiyelinin proton dip kuyuda kalabilsin diye dip kuyu ile asimetrik olduğu bilinmektedir. Mutasyonun gerçekleştirilebilmesi için, protonun sığ potansiyel duvarlarından tünellenmesi gerekmektedir. Protonun düzenli pozisyonundan hareketi tatometrik geçiş olarak tanımlanır. Eğer DNA kopyalanması bu durumda yer alırsa DNA için baz eşleştirme kuralı mutasyona sebep olabilecek bir tehlike oluşturabilir. Per-Olov Lowdin, çift sarmalda( kuantum biyolojisi) anlık DNA mutasyon teorisini geliştiren ilk kişidir. Kuantum tünelleme-indükleme nin biyolojideki diğer örnekleri kanser ve yaşlanmaya neden olduğuna inanılmaktadır.

Soğuk emisyon

Elektronların soğuk emisyonu fizikte yarı iletken ve süper iletkenler ile ilgilidir. Elektronların düzensizce metal yüzeyinden akan gerilime doğru atladığı çünkü diğer bariyerlerden sıradan çarpışmalar süresince istatistiksel olarak daha çok enerjili oldukları termodinamik emisyon ile benzer şekildedir. Elektrik alan çok büyük olduğu zaman, tünelin atomik durumun dışında olarak elektronlar için yeterli olacak şekilde, akımın yaklaşık olarak elektrik alanla üstel biçimde belirtilebileceği şekilde geçmesine izin verir. Bu materyaller flash bellekler, vakum tüpleri ve elektron mikroskopları için önemlidirler.

Tünel kavşağı

Basit bir bariyer iki iletkenin ince bir yalıtkan ile ayrılmasından oluşturulabilir. Bunlar kuantum tünelinin çalışması için gerekli olan tünel kavşaklarıdır. Josephson kavşağı kuantum tünellemesinden fayda sağlar ve bazı yarı iletkenlerin süper iletkenliği Josephson kavşağı için oluşturulur. Güneş pili çoklu kavşağında da olduğu gibi bu manyetik alan ve hassas voltaj ölçümlerinde birçok uygulamaya sahiptir.

Rezonans tünelleme cihazının potansiyel bariyerler boyunca kuantum tünellemesi olayına bağlı çalışma mekanizması.

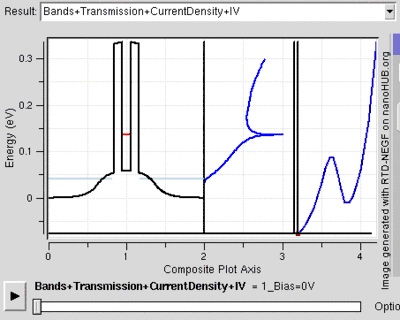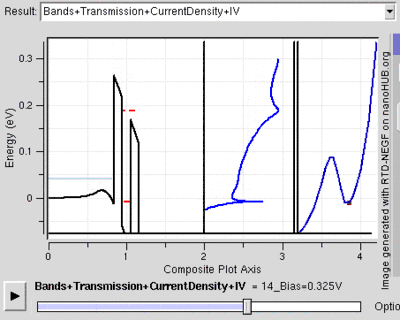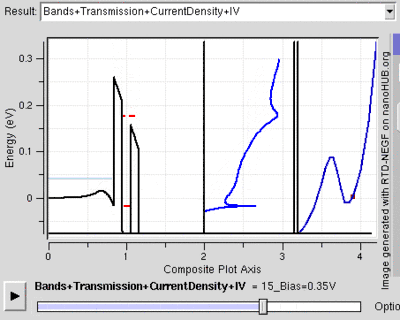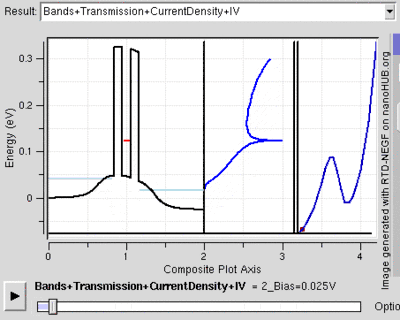
Tünel diyotu

Diyotlar elektrik akımının diğer yönlerden daha çok bir yöne gitmesini sağlayan elektrikli yarıiletken alettir. Bu alet amacına yönelik hizmet vermek için N tipi ve P tipi yarı iletken katmanlar arasındaki tükenme tabakasına dayanır. Bu ikisinin tükenme tabakasına ağır katkısı olduğu zaman tükenme tabaksı tünelleme için yeterince ince olabilir. Tünellemenin öneminden dolayı küçük bir sapma akıma uygulanır. Bunun maksimum enerjiye sahip olduğu yerde örneğin p ve n iletkenleri bağlar aynıdır. Gerilim arttıkça artık iletken bağlar sıralanamaz ve diyot tipik bir şekilde davranır.

Tünellenen akım hızlı şekilde aktığından dolayı, tünel diyotları gerilim aralığı artıp azalacak olan aralığa göre düzenlenir. Bu özellik bazı uygulamalarda kullanılır örneğin karakteristik tünelleme ihtimali gerilimin değişmesiyle değişir.

Rezonans tünelleme diyotu kuantum tünellemesini birçok benzer sonuçlara ulaşmak için de kullanılır. Diyot gerilimin ilerlemesi için fazla akımın bulunduğu yüksek enerjili iletkenlerin yan yana olduğu rezonans gerilimine de sahiptir. Bu en düşük enerji seviyesini gösteren kuantum potansiyel duvarını yaratır. Bu enerji elektronların enerjisinden daha yüksek olduğu zaman tünnelleme gerçekleşmez. İki gerilim enerjisinin hizalandığı anda elektronlar açık kablodaymış gibi akmaya başlar. Gerilim yükselirken tünelleme olanak dışı olmaya başlar ve ikinci enerji seviyesi fark edilebilir hale gelene kader diyot normal şekilde davranır.

Tünel-alan transistörü

Avrupa araştırma projesi kuantum tünellemesi ile kontrol edilen kanaların olduğu transistörün termal enjeksiyonlardan daha etkili bir alanı olduğunu gösterdi. Kanal gerilimini 1 volttan 0.2 volta ve güç tüketimini 100 kat daha azalttı. Eğer bu transistörler VLSI çipleri içinde büyütülürse performanslarını çok daha fazla geliştiriceklerdir.

Kuantum iletkenlikleri

Elektrik iletkenliğinin Drude modeli iletken metaldeki elektronların yapısı hakkında mükemmel tahminler yaparken, elektron çarpışmalarının doğasını anlamak için kuantum tünellemesi genişletilerek kullanılabilir. Serbest elektron paketleri bir dizi düzensiz dizilmiş bariyerle karşılaştığında %100 aktarma gerçekleşsin diye tüm bariyerler arasında bir müdahale olur. Teori şöyle söyler eğer dikdörtgen dizideki pozitif yüklü çekirdek metal boyunca tünnelencek serbest elektronlar yüksek derece de iletkenliğe izin verirler ve bu tür kirlilikler metali önemli derece de bozar.

Taramalı tünelleme mikroskobu

Taramalı tünelleme mikroskobu Gerd Binnig vr Heinrich Rohrer tarafından icat edilmiştir. Metal üzerindeki her bir atomu bireysel olarak gözlemleye izin verir. Uzaklık ile kuantum tünelleme arasındaki ilişkiden yararlanılarak kullanılır. Taramalı tünelleme mikroskobunun ucu iletken yüzeye çok yakın tutulduğu zaman, iğne ve yüzey arasındaki tünelleme elektron akımı ölçülerek bulunablir. Üzerine fazla miktarda gerilim uygulandığında ucunu aşabilen Piezoelektirk çubuk kullanılarak tünelleme akımını sabit bir düzeyde tutulabilir. Bu çubuklara uygulanabilen zamanla değişebilen gerilim kayıt edilebilir ve iletken yüzey fotoğraflanabilir. Taramalı tünelleme mikroskoplarının doğrulukları 0.001 nm veya %1 atomik yarıçaptadır.

Işıktan hızlı

Dönen sıfır parçacıkları için tünelleme anındaki seyahat ışık hızından fazla olacaktır. Görünüşe göre parçacığın ayrılmadan önce referans noktasına varacağı için nedensellik ilkesinin ihlali söz konusudur. Ancak dikkatle yapılan dalga paketlerinin aktarımının analizleri aslında görecelik ilkesinin ihlalinin olmadığını göstermektedir. 1988 de Francis E. Low sıfır zaman tünellemesini tekrar gözden geçirmiştir. Günümüzde yapılan fononlar, fotonlar ve elektronların deneysel tünellenmelerinin verileri Günter Nimtz tarafından yayınlanmıştır.

Kuantum tünellemesinin matematiksel yorumu

Aşağıdaki altbölümler kuantum tünellemesinin matematiksel formüllerini tartışmaktadır.

Schrödinger Denklemi

Tek boyutta zamandan bağımsız bir parçacık için Schrödinger denklemi şöyle yazılabilir

${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\Psi (x)+V(x)\Psi (x)=E\Psi (x)}$ or

${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)\Psi (x)\equiv {\frac {2m}{\hbar ^{2}}}M(x)\Psi (x),}$

${\displaystyle \hbar }$ Planck sabitidir. m parçacığın kütlesi, x parçacığın hareketi yönündeki mesafesi, Ψ Schrödinger dalga fonksiyonu, V parçacığın potansiyel enerjisi( uygun olan herhangi bir referans noktasına göre ölçülen), E parçacığın x eksenindeki hareketiyle alakalı enerjisi ve M(x), V(x) tarafından tanımlanan fizikte henüz bi ismi olmayan bir niceldir. M(x) in pozitif veya negatif değerli olmasına göre değişen Schrödinger’in denklemi farklı her x değeri için farklı bir değer alabilir. Eğer M(x) sabit ve negatif olursa, Schrödinger denklemi şu formda yazılır

${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x)=-k^{2}\Psi (x),\;\;\;\;\;\;\mathrm {where} \;\;\;k^{2}=-{\frac {2m}{\hbar ^{2}}}M.}$

Bu denklemin çözümü faz sabiti –k veya k ile birlikte hareket eden dalgayı verir. Alternatif olarak eğer M(x) sabit ve pozitif ise, Schrödinger denklemi şu şekilde yazılır

${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x)={\kappa }^{2}\Psi (x),\;\;\;\;\;\;\mathrm {where} \;\;\;{\kappa }^{2}={\frac {2m}{\hbar ^{2}}}M.}$

Bu denklemin çözümü fani dalgalarda artan ya da azalan üstel yapıda olabilir. M(x) in pozisyon ile alakalı olduğu durumlarda, M(x) in pozitif veya negatif olmasına bağlı olarak aynı farklılıklar meydana gelir. Ardından M(x) in işareti ortamı belirler. Pozitif M(x) için ortam A tanımlanırken, negatif M(x) için ortam B tanımlanır. Bundan dolayı eğer pozitif M(x) in alanı iki negatif M(x)in alanı arasında sıkıştırılmışsa fani dalga kuramı oluşur ve bu da potansiyel bariyer yaratır.

Bu olay M(x) in x e bağlı çok karmaşık durumlarda olduğu matematikte, bazı özel durumlar hariç, fiziksel gerçekçilikte karşılık bulamamaktadır. Yarı klasik metotların fizik kitaplarında olduğu gibi tartışımı diğer bölümde verilecektir. Tamamı ile ve karmaşık matematiksel işlemler 1965 yılında Fröman tarafından ortaya çıkmıştır. Fikirleri fizik kitaplarında anonim değildir fakat düzeltmeleri nicel efektler taşır.

WKB yaklaşımı

Dalga fonksiyonu üstel bir fonksiyon olarak açıklanır.

${\displaystyle \Psi (x)=e^{\Phi (x)}}$, where ${\displaystyle \Phi ''(x)+\Phi '(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right).}$

${\displaystyle \Phi '(x)}$ gerçek ve hayali olarak iki kısma ayrılmıştır:

${\displaystyle \Phi '(x)=A(x)+iB(x)}$, A(x) B(x) gerçek değerli fonksiyonlar için.

İkinci denklemi birinci denklemin içine yerleştirerek ve hayali kısmın bölümünü kullanarak

${\displaystyle A'(x)+A(x)^{2}-B(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}$.

Bu denklemi çözmek için her iki kısımda yarı klasik yaklaşımlar yapılarak ${\displaystyle \hbar }$ üstel serisinde genişletilmelidir. Denklemden üstel serinin denklemin gerçek kısmını sağlaması için en az ${\displaystyle \hbar ^{-1}}$ birinci dercesiyle, iyi bir klasik limit için de Planck sabitinin olabildiğinde tüksek bir derceyle başlatılması şuna izin verir

${\displaystyle A(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}A_{k}(x)}$

ve

${\displaystyle B(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}B_{k}(x)}$,

En düşük mertebeden terimler ile aşağıdakiler takip etmekte,

${\displaystyle A_{0}(x)^{2}-B_{0}(x)^{2}=2m\left(V(x)-E\right)}$

ve

${\displaystyle A_{0}(x)B_{0}(x)=0}$.

Bu noktada iki aşırı durum hesaba katılabilir. ‘’’Durum 1’’’ Eğer faz ${\displaystyle A_{0}(x)=0}$ ya kıyasla genlik çok yavaşsa:

${\displaystyle B_{0}(x)=\pm {\sqrt {2m\left(E-V(x)\right)}}}$

Klasik hareket içindir. Genişleme verimin bir sonraki mertebesi ile tekrar çözümü

${\displaystyle \Psi (x)\approx C{\frac {e^{i\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(E-V(x)\right)}}+\theta }}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(E-V(x)\right)}}}}$

‘’’durum 2’’’ Eğer genliğine kıyasla faz yavaş şekilde değişirse ${\displaystyle B_{0}(x)=0}$ ve

${\displaystyle A_{0}(x)=\pm {\sqrt {2m\left(V(x)-E\right)}}}$

Tünellemeye karşılık gelir. Genişleme veriminin bir sonraki mertebesi ile tekrar çözümü

${\displaystyle \Psi (x)\approx {\frac {C_{+}e^{+\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}+C_{-}e^{-\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}}$

İki durumda da paydalardan görülmektedir ki iki yaklaşık çözümlerde klasik dönüm noktası E=V(x) e yakındır. Potansiyel tepeden uzakta parçacık serbest ve salınım yapan dalgaya benzer davranır, potansiyel tepenin altında, parçacık genlik içinde üstel değişikliklere gider. Bu limitlerde parçacığın davranışlarını hesaba katarak ve klasik dönüş noktalarını hesaba katarak genel bir çözüm yapılabilir. Başlangıç için klasik dönüş noktası ${\displaystyle x_{1}}$ seçilir ${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}$ serisinin içinde genişletilir ${\displaystyle x_{1}}$:

${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1})+v_{2}(x-x_{1})^{2}+\cdots }$

Birinci dereceden terim tutulması doğrusallık sağlar:

${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1})}$.

Bu yaklaşım kullanılarak, ${\displaystyle x_{1}}$ denklemi diferensiyel denklem olur:

${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)=v_{1}(x-x_{1})\Psi (x)}$.

Çözüm olarak Airy fonksiyon kullanılarak bu denklem çözülebilir.

${\displaystyle \Psi (x)=C_{A}Ai\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)+C_{B}Bi\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)}$

Bu çözümleri tüm klasik dönüm noktaları için alarak sınırlı çözümlerle bağlantılı genel bir sonuç elde edilebilir. Klasik dönüm noktasının bir tarafında verilen 2 katsayı,diğer tarafında verilen 2 katsayı kullanılarak bunların birleştirilerek elde edilen sonucuyla karar verilebilir. Sonuç olarak, Airy fonksiyon çözümü sinüsün kosünüsün ve üstel fonksiyonun belirli sınırlar içinde asimptotu olur. ${\displaystyle C,\theta }$ ve ${\displaystyle C_{+},C_{-}}$ aralarındaki ilişki

${\displaystyle C_{+}={\frac {1}{2}}C\cos {\left(\theta -{\frac {\pi }{4}}\right)}}$

ve

${\displaystyle C_{-}=-C\sin {\left(\theta -{\frac {\pi }{4}}\right)}}$

Katsayının bulunmasıyla genel çözüm bulunabilir. Böylece tek bariyer boyunca tünellenen parçacığın dağıtım katsayısı

${\displaystyle T(E)=e^{-2\int _{x_{1}}^{x_{2}}\mathrm {d} x{\sqrt {{\frac {2m}{\hbar ^{2}}}\left[V(x)-E\right]}}}}$,

${\displaystyle x_{1},x_{2}}$potansiyel bariyer için 2 klasik dönüm noktası Dikdörtgen bariyer için bu açıklama şöyle ifadelenmiştir:

${\displaystyle T(E)=e^{-2{\sqrt {{\frac {2m}{\hbar }}(V_{0}-E)}}(x_{2}-x_{1})}={\tilde {V}}_{0}^{-(x_{2}-x_{1})}}$.

Konuyla ilgili yayınlar

• N. Fröman and P.-O. Fröman (1965). JWKB Approximation: Contributions to the Theory. Amsterdam: North-Holland.
• Razavy, Mohsen (2003). Quantum Theory of Tunneling. World Scientific. ISBN 981-238-019-1.
• Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd bas.). Prentice Hall. ISBN 0-13-805326-X.
• James Binney and Skinner, D. (2010). The Physics of Quantum Mechanics: An Introduction (3rd bas.). Cappella Archive. ISBN 1-902918-51-7.
• Liboff, Richard L. (2002). Introductory Quantum Mechanics. Addison-Wesley. ISBN 0-8053-8714-5.
• Vilenkin, Alexander; Vilenkin, Alexander; Winitzki, Serge (2003). "Particle creation in a tunneling universe". Physical Review D. 68 (2). s. 023520. arXiv:gr-qc/0210034 $2. Bibcode:2003PhRvD..68b3520H. doi:10.1103/PhysRevD.68.023520.

Dış bağlantılar

• Animation, applications and research linked to tunnel effect and other quantum phenomena25 Mayıs 2012 tarihinde Wayback Machine sitesinde arşivlendi. (Université Paris Sud)
• Animated illustration of quantum tunnelling
• Animated illustration of quantum tunnelling in a RTD device