Lineer interpolasyon

Lineer interpolasyon, lineer polinomlar kullanarak, dataların bilindiği noktalardan yeni dataların üretilmesini sağlayan bir eğri uydurma metodudur.

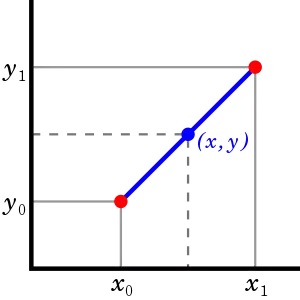
İki kırmızı nokta, datanın değerini bildiğimiz koordinatlar ve mavi çizgi, bu iki koordinat arasındaki lineer doğrudur. (x, y) noktasındaki bilmediğimiz data değeri iki kırmızı nokta değerlerinden lineer interpolasyon yöntemiyle bulunabilir.

Bilinen iki nokta arasında lineer interpolasyon
Bu geometrik gösterimde, yeşil noktanın değerinin kırmızı ve mavi noktalar arası uzaklık ile çarpımı, kırmızı nokta değerinin yeşil ve mavi noktaları arası uzaklık ile çarpımı ila mavi nokta değerinin yeşil ve kırmızı noktaları arası uzaklık ile çarpımının toplamına eşittir.

Koordinatları ve olan bilinen iki nokta arasındaki düz çizgi, lineer interpolant olarak isimlendirilir. aralığındaki bir x değeri için, düz çizgi üzerindeki y değeri aşağıdaki denklem ile verilir:

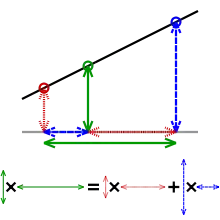
Bu denklem, geometrik olarak sağdaki figürden türetilebilir. Lineer interpolasyon, polinom interpolasyonun n = 1'e ait özel çözümüdür.

Yukarıdaki denklem x'e ait bir bilinmeyen olan y değeri için çözülürse:

Bu formül, aralığı için lineer interpolasyon formülüdür. Aralığın dışında ise, formül lineer ekstrapolasyon formülü haline gelir.

Bu formül, aynı zamanda, ağırlıklı ortalama (İng. "weighted average") olarak düşünülebilir. Ağırlıklar değer aralığı uç noktalarından bilinmeyen noktaya olan uzaklıkla ters orantılıdır. Bir başka deyişle, yakın bir nokta uzak bir noktaya göre daha fazla ağırlığa (etkiye) sahiptir.

Ağırlıklar, ve olarak ifade edilebilir. Bu terimler, bilinmeyen noktadan, değer aralığı uç noktalarına olan normalize uzaklıktır. Terimlerin toplamı 1'e eşit olduğundan, yukarıda elde edilen lineer interpolasyon formülü şu şekilde türetilebilir:

Bir data setinin interpolasyonu
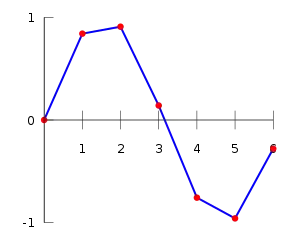
Bir data seti (kırmızı noktalar) lineer interpolasyonu , lineer interpolant parçalarından (mavi çizgiler) oluşur.

(x0, y0), (x1, y1), ..., (xn, yn)'den oluşan bir data setinin lineer interpolasyonu, dataya ait nokta çiftlerinden oluşan lineer interpolantların uç uca eklenmesi olarak tanımlanır. Bu, türevi (genellikle) süreksiz, diferansiyellenebilirlik sınıfı olan bir sürekli eğriyi üretir.

Yaklaşım (approximation) olarak lineer interpolasyon

Lineer interpolasyon, sıkça, iki noktada değeri bilinen bir f fonksiyonunun bir değerini yaklaşık olarak hesaplamakta kullanılır. Bu yaklaşıma ait hata (İng. "error") aşağıdaki gibi tanımlanır:

Bu denklemde, p lineer interpolasyonun polinomudur:

Hata sınırları, eğer f sürekli bir ikinci türeve sahipse, Rolle teoremi kullanılarak aşağıdaki gibi hesaplanabilir:

Görüleceği üzere, bir fonksiyona ait iki nokta arasındaki bir yaklaşımın niteliği, fonksiyonun ikinci türevine bağlıdır. Dolayısıyla, sert ve çok kıvrımlara sahip bir fonksiyon, az kıvrımlara sahip bir fonksiyona göre, lineer interpolasyonla, daha az bir nitelikte bir (kötü) yaklaşımı üretilebilir.

Uygulamalar

Lineer interpolasyon, genellikle bir değer tablosundaki ara boşlukları doldurmak için kullanılır. Örneğin, bir ülkenin 1970, 1980, 1990 ve 2000 yılındaki nüfusunu veren bir tablodan, 1994 senesi nüfusunu tahmin etmek, lineer interpolasyon ile mümkün olabilir.

Yanı sıra, bilgisayar grafik uygulamalarında lineer interpolasyon sıklıkla kullanılır. Lineer interpolasyon, bu konunun teknik jargonunda, bazen lerp olarak adlandırılır. Bu terim, İngilizce'de fiil ya da isim olarak kullanılabilir: ör. "Bresenham's algorithm lerps incrementally between the two endpoints of the line."

Lerp fonksiyonu, tüm modern bilgisayar grafik işlemcilerinin donanımına yükleniktir. Sıklıkla, bunlar daha karmaşık fonksiyonların yapıtaşı olarak kullanılır: örneğin, bir bilineer interpolasyon üç lerp ile tamamlanır. Bu fonksiyonun kullanılmasına, (kaynakları kullanma seviyesi olarak) ucuz ve kolay olduğu için, sürekli fonksiyonlarda hızlıca arabul için çok fazla maddeye (elemana ya da data noktasına) ihtiyaç duymadan doğruluk seviyesi yüksek bir başvuru çizelgesi yaratılmasında başvurulabilir.

Ek konular
Lineer, bilineer, ve 1- ila 2-boyutlu interpolasyonların mukayesesi. Sırası ile, siyah ve kırmızı/sarı/yeşil/mavi noktalar interpole edilmiş nokta ile komşu noktaları göstermektedir. Yükseklikler, noktaların değerlerini temsil etmektedir.

Doğruluk

Eğer bir C0 fonksiyonu yetersiz ise, örneğin C0'dan daha çalkantısız data değerleri üreten bir process varsa, lineer interpolasyon çoğunlukla bağ interpolasyonu ile ya da bazı hallerde polinom interpolasyon yer değiştirir.

Çok değişkenlilik

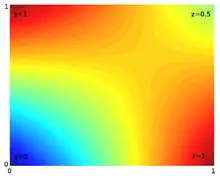
Lineer interpolasyon, buraya kadar sadece bir konumsal boyutlu (İng. "spatial dimension") data noktaları için açıklandı. İki konumsal boyut için (düzlem), lineer interpolasyon bilineer interpolasyona; üç konumsal boyut için (hacim) trilineer interpolasyona evrilir. Dikkat edilmesi gereken husus ise, bu interpolantların artık konumsal koordinatların lineer fonksiyonu olmadığıdır. Aksine, lineer fonksiyonların çarpımlarından müteşekkildirler.

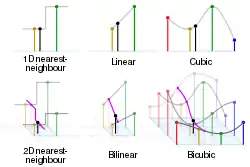
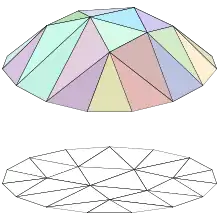
Lineer interpolasyonun diğer dönüşmüş tanımlarına, üçgensel ve dörtyüzlü meşlerde, örneğin Bézier yüzeyleri'nde rastlanabilir. Bu dönüşümler, çok-boyutlu parçalı lineer fonksiyon olarak adlandırılır (en alt figüre bakınız).

Birim bir kare üzerindeki bir bilineer interpolasyon örneği. z-değerleri 0, 1, 1, ve 0.5'tir. İnterpolasyon değerleri renkle gösterilmiştir.
İki-boyutta bir parçalı lineer fonksiyon (üstte) ve lineer formda konveks çokgenler (altta).

Tarihçe

Antik dönemlerden beri lineer interpolasyon kullanılmaktadır. Başlıca kullanım gereği astronomi data setlerindeki boşlukların doldurulmasıdır.

Babilli astronom ve matematikçilerin Seleukos Mezopotamyası'nda (milattan önce son üç yüzyıl), ve Yunan astronom ve matematikçi Hipparkos'un (M.Ö. 200 civarı) lineer interpolasyon kullanmış olduğu düşünülmektedir.

Lineer interpolasyonun bir tanımı/açıklaması Ptolemy'in Almagest adlı eserinde (M.S. 200 civarı) yer alır.

Programlama dillerinde

Pek çok library, lerp fonksiyonunu içerir: ör. verilen iki girdiden (v0,v1) kapalı birim aralık [0,1] içinde yer alan bir parametre (t) için interpolasyon çıktı edilebilir:

// Imprecise method which does not guarantee v = v1 when t = 1, due to floating-point arithmetic error.
// This form may be used when the hardware has a native Fused Multiply-Add instruction.
float lerp(float v0, float v1, float t) {
  return v0 + t*(v1-v0);
}

// Precise method which guarantees v = v1 when t = 1.
float lerp(float v0, float v1, float t) {
  return (1-t)*v0 + t*v1;
}

Bu lerp fonksiyonu alpha blending için (parametre t, alpha değeridir) sıklıkla kullanılan bir fonksiyondur. Bu formülasyon, bir vektörün çoklu bileşenlerinin harmanlanması için genişletilebilir (ör. konumsal olarak x, y, z eksenlerinde veyahut r, g, b renk bileşenlerinde).

Ayrıca bakınız

Kaynakça
    • Meijering, Erik (2002), "A chronology of interpolation: from ancient astronomy to modern signal and image processing", Proceedings of the IEEE, 90 (3), ss. 319-342, doi:10.1109/5.993400.

    Dış bağlantılar
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.