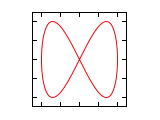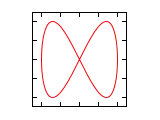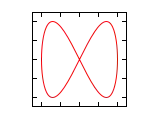Lissajous eğrileri

Elektronikte Lissajous eğrileri iki farklı periyodik fonksiyon tarafından osiloskop ekranında oluşturulan şekillerdir. Bu şekillere adını veren kişi bu fonksiyonları 1857 yılında inceleyen Fransız fizikçi Jules Antonie Lissajous'tur (1822-1880).

Osiloskop ekranında Lissajous eğrisi

Çift girişli osiloskop

Normal koşullar altında bir osiloskoba giren sinyal y eksenine uygulanır. x ekseni ise kullanıcı tarafından denetlenen zaman eksenidir. Ancak kimi osiloskoplarda y eksenine ek olarak x eksenine de giriş yapma imkânı vardır. Bu durumda artık x ekseni zaman ekseni değildir. Hem y hem de x eksenine giriş yapıldığı zaman ekranda oluşan şekil Lissajous eğrisidir.

Matematiksel gösterim

${\displaystyle f_{x}=A\cdot sin(at+\phi )}$

${\displaystyle f_{y}=B\cdot sin(bt)}$

Bu ifadelerde;

A,B: Sinyalerin genliği

a,b: Sinyallerin açısal frekansları

${\displaystyle \phi }$: t₀ anında iki sinyal arasındaki faz farkı

Eğrinin türü a/b oranına, iki sinyal arasındaki faz farkına ve katsayılara bağlıdır. Mesela

Şayet a=b ise şekil elipstir.

Şayet a=b, A=B ve ${\displaystyle \phi =\pi /2}$ ise şekil çemberdir.

Şayet a=b ve ${\displaystyle \phi =0}$ ise şekil bir doğrudur.

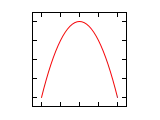
Şayet b=2a ve ${\displaystyle \phi =\pi /4}$ ise şekil paraboldur.

Şayet a/b oranı irrasyonel sayı ise bu durumda ekranda sabit bir şekil olmaz.

Galeri

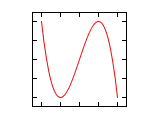
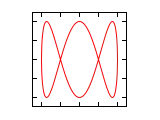
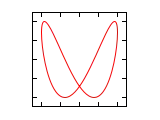
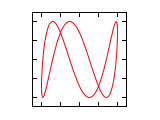
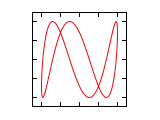
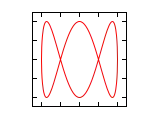
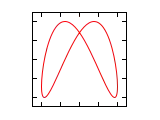
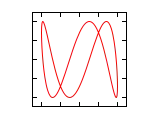
Farklı a/b oranları ve radyan cinsi faz açıları için Lissajous eğrileri aşağıda gösterilmiştir.

Faz farkı (${\displaystyle \phi }$)	a/b =1:1	a/b =1:2	a/b =1:3	a/b =2:1
0
¹/₄·π
¹/₂·π
³/₄·π
1·π
1¹/₄·π
1¹/₂·π
1³/₄·π
2·π

A ve B ekrandaki şeklin genişliği veya yüksekliğini denetler.