Doğru (geometri)

Doğru, matematikte mantıksal bir değer. Matematik'te ne olduğu belli olmayan (tanımsız) değerlerden biridir. Hakkında doğru veya doğru değil diye değer yükleyebileceğimiz cümlelerden mümkün olduğu kadar azına "doğru" değeri veririz. Sonra mantıki olarak yeni cümlelerin değerlerini araştırırız. Ayrıca geometride ifadesi aynı doğrultuda olan ve her iki yönden de sonsuza kadar giden noktalar kümesi diye de tanımlanır. Bir doğru üzerinde en az 2 nokta, dışında da en az 1 nokta mevcuttur.

Tanım

Matematikte doğrunun değişik ifadeleri vardır:

• Bir noktalar kümesidir.
• Cetvel yardımıyle çizilen çizgi, iki nokta arasındaki gergin bir ip doğruyu belirtir.
• Farklı 2 noktadan yalnız bir doğru geçer.
• Farklı 2 nokta yalnız bir doğru belirtir.
• Farklı 2 düzlem en fazla bir doğruda kesişir.

Örnekler

Üç doğru

${\displaystyle y=mx+b\,}$

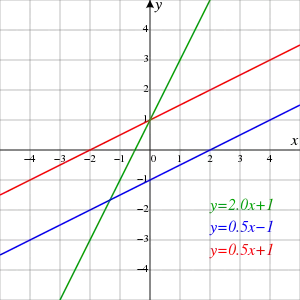
burada:

m doğrunun eğimi.

b doğrunun düşey eksenle kesişme noktası.

x y fonksiyonunun bağımsız değişken.

Üç boyutluda, bir doğru genellikle parametrik eşitlikler olarak ifade edilir:

${\displaystyle x=x_{0}+at\,}$

${\displaystyle y=y_{0}+bt\,}$

${\displaystyle z=z_{0}+ct\,}$

burada:

x, y ve z, tden bağımsız fonksiyonlardır.

${\displaystyle x_{0}}$, ${\displaystyle y_{0}}$, ve ${\displaystyle z_{0}}$ her biri kendi değişken olan birincil değerlerdi.

a, b, ve c doğrunun eğimine bağlıdırlar, böylece vektör (a, b, c) doğruya paraleldirler.

Geleneksel tanım

R²de, tüm doğrular L ile tanımlanır.

${\displaystyle L=\{\mathbf {a} +t\mathbf {b} \mid t\in \mathbb {R} \}}$

Özellikleri

${\displaystyle L=\{(x,y)\mid ax+by=c\}\,}$

Genişlemeleri

Işın

Bir ışın örneği

Bir ucu sınırlı olan doğrudur. Diğer bir deyişle, bir başlangıç noktası olan ve o noktadan sonsuza doğru uzanan noktalar kümesidir. Bir doğrunun üzerinde bir nokta alıp, doğruyu o noktadan ikiye ayırdığımızda iki adet ışın elde ederiz.

Soldaki örnekte; A ucundan sınırlanmış B, C doğrultusunda, C noktasından sonsuza doğru giden bir ışındır. A ve B noktaları açık, C noktası kapalıdır. Bunun anlamı A ve B noktaları ışına dahil değildir. Işın o noktaları kapsamamaktadır.

Ayrıca bakınız

• Matematiksel şekillerin listesi