Smith abağı
Smith abağı veya Smith diyagramı (Smith chart), radyo ve mikrodalga frekanslarındaki iletim hatlarının tasarımı ve empedans eşlemesinde kullanılan bir grafiktir.[1] Elektrik-elektronik ve haberleşme mühendisleri tarafından kullanılan bu abak Phillip H. Smith (1905–1987) tarafından icat edilmiştir.[2][3] Smith abağı aynı anda empedans, admitans, yansıma ile saçılma katsayıları (), kazanç konturu ve stabilite gibi çok sayıda parametreyi aynı anda gösterebilmektedir; bu yüksek frekans devreleri dışında mekanik titreşim analizinde de kullanılmasını sağlamıştır.[4][5] Smith abağı genelde birim yarıçap içinde kullanılır; buna karşın abağın geri kalanı da elektronik osilatör ve stabilite analizinde kullanılmaktadır.[6]

Her ne kadar günümüzde Smith abağı ile empedans eşleme hesaplama problemleri çoğunlukla yazılımlar aracılığıyla çözülse de abak halen RF parametrelerinin bir veya birden fazla frekansta nasıl değiştiğinin gösterilmesinde kullanılmaktadır. Çoğu yüksek frekans devre analizi yazılımı ve empedans ölçme aletleri sonuçları Smith abağı'nda gösterebilmektedir.
Genel bilgiler

Smith abağı iki boyutlu karmaşık yansıma katsayısı düzleminde çizilir. Abak genel olarak empedansa, bazen de admitansa veya ikisine göre göre normalize edilir; bunlar Z, Y ve ZY Smith abakları olarak bilinir.[7] Bu normalizasyon abağın herhangi bir karakteristik ya da sistem empedansına göre kullanılabilmesini sağlar; karakteristik empedans abağın orta noktasına tekabül eder. En genel normalizasyon empedansı 50 ohm'dur. Smith abağından elde edilen sonuç direkt karakterize empedans ya da admitans ile çarpılarak asıl sonuca dönüştürülebilir; aynı zamanda birimsiz değişken olan yansıma katsayıları abaktan direkt okunabilmektedir.
Smith abağı dalga boyu ve açıya göre çevresel bir şekilde ölçeklendirilmiştir. Dalga boyu ölçeği dağıtılmış elemanlı devreler için kullanılır; hat uzunlığı bu devrelerde sinyal jeneratörü ve ilgili yük arasındaki uzaklık olarak alınır. Açı ölçeği ise voltaj yansıma katsayısının açısı için kullanılır. Abak aynı zamanda toplu devre elemanlarının analizi ve eşlemesinde de kullanılabilir. Smith abağının kullanımı alternatif akım ve iletim hattı teorisine hakim olmayı gerektirmektedir.
Empedans ve admitans her frekansta değiştiğinden, Smith abağı aynı anda sadece tek bir frekans için kullanılabilir; sonuç abaktaki bir nokta olarak gösterilir. Bu genellikle dar bant (bant genişliği %5 ile %10 arası olan) devreler için yeterlidir; daha gen,ş bant aralıkları için banttaki birden fazla frekans abakta analiz edilmelidir. Yakın frekanslarda yapılan frekanslarda elde edilen noktalar birleştirilerek bir gezenek oluşturulabilir.
Smith abağındaki farklı frekans noktalardan oluşan bir gezenek sistemle ilgili farklı detaylar verebilir:
- yükün frekans bandında ne kadar kapasitif veya endüktif olduğu
- farklı frekanslarda empedans eşleme uyumluluğu
- yükün sisteme ne kadar iyi eşlendiği
Çok sayıda noktanın bulunduğu empedans ve admitans grafiklerde Smith abağının doğruluğu azalır; bu bazı durumlarda farklı ölçekleme ile telafi edilebilir.
Matematiksel temelleri
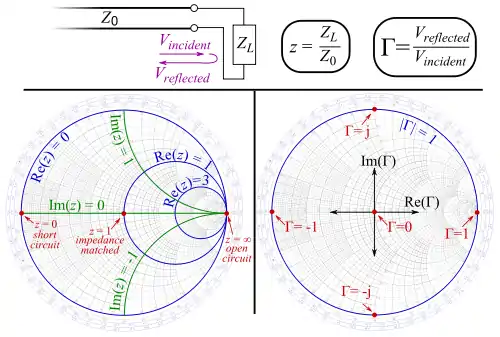
Normalize empedans ve admitans
Karakteristik empedansı olan bir iletim hattının karakteristik admitansı ile ifade edilir. Bu ikisi,
eşleniğiyle bağlıdır. Ohm biriminde bir empedansı karakteristik empedansına bölünerek normalize empedansına (zT) çevrilebilir:
Normalize admitans için benzer bir formül bulunur:
Empedansın SI birimi ohm (Ω) ve admitansın birimi ise siemens'tir (S). Normalize empedans ve admitans ölçüsüzdür. Empedans ve admitansın Smith abağı kullanılmadan önce normalize edilmesi gerekir; abaktan elde edilen sonuç daha sonra karakteristik değerle çarparak asıl sonuca çevrilebilir.
Normalize empedans Smith abağı
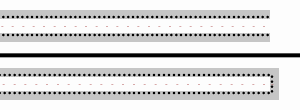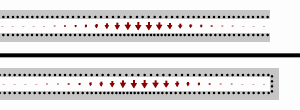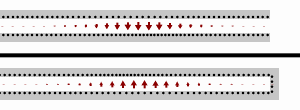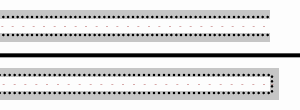
İletim hattı teorisine göre bir iletim hattı karakteristik empedanstan () farklı bir empedansla () sonlandırılırsa, bir duran dalga oluşur. Bu dalga hem ilerleyen () hem de yansıyan () dalgaların toplamıyla oluşur. Bu voltajlar kompleks üstel sayılarla ifade edilebilir:
- ve
Bu denklemlerleki ilgili ifadeler:
- dalganın zamana bağlı kısmına,
- dalganın uzaya bağlı kısmına,
- açısal frekansa (rad/s),
- frekansa (Hz),
- zamana (s),
- ile sabitlere ve
- ise yük ile sinyal jeneratörü arasındaki hat mesafesine (m) tekabül eder.
Ayrıca iletim katsayısını (1/m) ifade etmektedir. Bu denklemde,
Smith abağı bir anda tek bir frekans () için kullanılır; bu şekilde dalganın zamana bağlı kısmı () sabit kalır. Tüm terimler bu değerle çarpılınca ani değer elde edilebilir. Bu değer bu frekanstaki tüm dalgalar için ortak olduğundan ihmal edilebilir:
- and
Bu denklemde ve yükte sırasıyla ileri ve geri giden voltaj genliklerini gösterir.
Karmaşık yansıma katsayısının hat boyunca değişimi
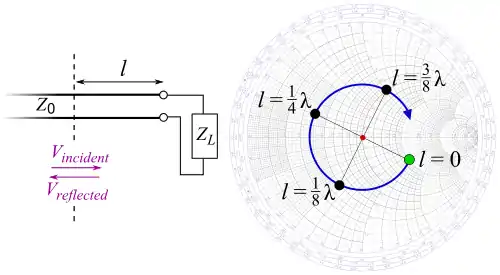
Karmaşık yansıma katsayısı yansıyan dalga ile ileri giden dalganın oranı ile hesaplanır. Bu göz önünde bulundurularak,
eşitliği tanımlanabilir; C bu denklemde sabit bir sayıdır.
'nın sabit olduğu tek biçimli bir iletim hattında duran dalganın karmaşık yansıma katsayısı hattaki pozisyona göre değişir. Eğer dalga kayıplı ise ( sıfırdan farklı ise), empedans değişiklikleri bir spiral ile ifade edilir. Smith abağı gerektiren çoğu problemde kayıplar ihmal edilebilecek kadar küçüktür (). Buna karşın kayıplı durumlarda karmaşık yansıma katsayısı şu hali alır:
Bu denklemde yükteki yansıma katsayısını ve ise yük ile yansıma katsayısı arasındaki hat uzaklığını ifade eder. Faz katsayısı ise,
olarak yazılabilir. Bu denklemde test frekansının iletim hattı içindeki dalga boyudur.
Bu göz önünde bulundurulacak genel yansıma katsayısı ifadesi,
olarak ifade edilebilir. Bu denklem, bir duran dalgada karmaşık yansıma katsayısı ve empedansın hat üzerinde her yarım dalga boyunda bir tekrar ettiğini gösterir. Karmaşık yansıma katsayısına genelde sadece yansıma katsayısı denir. Abağın dışındaki ölçeği dalga boyuna göre oranlanmıştır ve jeneratörden yüke olan uzaklığı belirtir; sıfırdan 0.50 'a göre oranlanmıştır.
Normalize empedansın hattaki pozisyonuna göre değişimi
Eğer ile hat boyuncaki voltaj ve hat sonuna giren elektrik akımı olarak tanımlanırsa, ilerleyen voltaj ile yansıyan voltaj
- and
eşitlikleri ile ifade edilebilir. Bu denklemler bölünür ve voltajların yerine voltaj yansıma katsayısını koyulursa
ve hattın sonundaki normalize empedansı olarak tanımlanırsa,
empedans formülü elde edilebilir:
- .
Alternatif olarak, yansıma katsayısını kullanarak aşağıdaki eşitlik yazılabilir:
Empedans Smith abağı bu denklemler ile ifade edilir. Matematiksel olarak ve Möbius dönüşümleri ile birbirine bağlıdır..
ve birimleri olmadan karmaşık sayılar ile gösterilir. Frekansa bağlı olarak değiştiklerinden hesaplandıkları frekanslar karakteristik empedanslarla birlikte belirtilmelidir. ayrıca karmaşık düzlemde açı ve genlik olarak ifade edilebilir. Yansıma katsayısının genliğinin 1'e eşit ya da 1'den küçük olması gerekir; bundan yola çıkarak katsayı çemberin içinde bir nokta olarak ifade edilebilir. Smith abağının ölçekleri abağın kutupsal bir grafik olarak kullanılabilmesini sağlar.
Eşlenmemiş, kayıpsız hattın denklemi,
kayıpsız hattın normalize empedans ile yansıma katsayısı formülü
- .
ve Euler formülü kullanılarak,
kayıpsız iletim hattı denklemi türetilebilir.[8]
Burada , ile sonlandırılan uzunluğunda kayıpsız bir iletim hattının girişinde görülen empedansı ifade eder. Bu denklemin eşleniği kayıpsız admitans ile her ikisi için kayıplı durumlarda türetilebilir.
Z Smith abağının bölgeleri
Eğer küresel diyagram bir Kartezyen koordinat sistemi'nin ortasına yerleştirildiyse, genel olarak açılar pozitif x aksına göre saat yönünün tersi bir şekilde ölçülür. Smith abağı da aynı şekilde ölçülmektedir; pozitif x aksı abağın ortasında noktasından başlayarak noktasına kadar uzamaktadır. x aksının üstündeki bölge endüktif empedansları (pozitif sanal kısım) ve altındaki bölge ise kapasitif empedansları (negatif sanal kısım) gösterir.
Hattım tamamen eşlenmesi durumunda yansıma katsayısı sıfırlanır; bu abağın ortasındaki "0 yarıçaplı bir daire" ile gösterilir. Hattın bir açık ay da kısa devre ile sonlandırılması durumunda tüm güç yansır ve katsayı birim çember üzerinde bir yerde durur.
Sabit normalize direnç ve reaktans çemberleri
Normalize empedans abağı sabit normalize direnç ve reaktans çemberlerinden oluşur. Abak, karmaşık yansıma düzleminde merkezdeki bir birim çemberinde bulunur; Kartezyen koordinat sisteminde bu daire x aksında (+1,0) ile (−1,0) noktaları ve y aksında (0,+1) ile (0,−1) noktalarından geçer.
ile karmaşık sayı olduğundan,
şeklinde yazılabilir; burada a, b, c ve d gerçel sayılardır.
Bunlar normalize empedans ve yansıma sabiti formüllerine yerleştirilirse,
yansıma katsayısı parametrelerin gerçel ve sanal kısımları ile ifade edilebilir:
- .
Bu denklem yansıma katsayısının normalize empedansa göre değişimini ifade eder ve abağı oluşturan çemberlerin Kartezyen bir sistemde çiziminde kullanılabilir.[9]
Y Smith abağı
Y Smith abağı Z abağına benzese de bu grafikte normalize admitans kullanılır. Normalize admitans yT, normalize empedans zT'nin çarpımsal tersidir:
Bu göz önünde bulundurularak
ve
eşlenikleri yazılabilir.
Y Smith abağı normalize empedans grafiği ile aynı şekilde gözükse de ölçeği 180° döndürülmüştür; numerik ölçeği aynı kalır. x aksının üstündeki bölge kapasitif, altındaki bölge de endüktif admitansları gösterir. Kapasitif admitansların sanal kısmı pozitif, endüktiflerin ise negatiftir.
Hattın sonunun tamamen eşlenmesi durumunda empedans abağında olduğu gibi yansıma katsayısı sıfırlanır; hattın açık veya kısa devrelenmesi durumunda voltaj yansıma katsayısı birim çemberde bulunur.
Yansıma katsayısı ve normalize empedans örnekleri
Yansıma katsayısının genliği 0.63 ve açısı 60° olan bir nokta kutupsal şekilde olarak gösterilir; bu abaktaki açı ölçeğini bularak ve birim çemberinin yarı çapına göre oranlama yaparak çizilebilir. Aşağıdaki tabloda bir empedans Smith abağındaki bazı noktaların kutupsal yansıma katsayıları ve dikey gösterimli normalize empedansları verilmiştir.
| Nokta | Yansıma katsayısı (kutupsal) | Normalize empedans (dikey) |
|---|---|---|
| P1 (Endüktif) | ||
| P2 (Endüktif) | ||
| P3 (Kapasitif) |
Kaynakça
- Ramo, Whinnery and Van Duzer (1965); "Fields and Waves in Communications Electronics"; John Wiley & Sons; pp 35-39. ISBN
- Smith, P. H.; Transmission Line Calculator; Electronics, Vol. 12, No. 1, pp 29-31, January 1939
- Smith, P. H.; An Improved Transmission Line Calculator; Electronics, Vol. 17, No. 1, p 130, January 1944
- Pozar, David M. (2005); Microwave Engineering, Third Edition (Intl. Ed.); John Wiley & Sons, Inc.; pp 64-71. 0-471-44878-8.
- Gonzalez, Guillermo (1997); Microwave Transistor Amplifiers Analysis and Design, Second Edition; Prentice Hall NJ; pp 93-103. 0-13-254335-4.
- Gonzalez, Guillermo (1997) (op. cit);pp 98-101
- Gonzalez, Guillermo (1997) (op. cit);p 97
- Hayt, William H Jr.; "Engineering Electromagnetics" Fourth Ed; McGraw-Hill International Book Company; pp 428–433. 0-07-027395-2.
- Davidson, C. W.;"Transmission Lines for Communications with CAD Programs";Macmillan; pp 80-85. 0-333-47398-1
Ek kaynaklar
- Mizuhashi, T., Theory of four-terminal impedance transformation circuit and matching circuit, The Journal of the Institute of Electrical Communication Engineers of Japan, pp. 1053–1058, December 1937.
- P.H.Smith 1969 Electronic Applications of the Smith Chart. Kay Electric Company
- G. A. Campbell, "Cisoidal Oscillations", Proc. AIEE, 30, 1-6, pp. 789–824 (1911).
Dış kaynaklar
| Wikimedia Commons'ta Smith charts ile ilgili ortam dosyaları bulunmaktadır. |
- Mathematical Construction and Properties of the Smith Chart12 Haziran 2020 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce)
- Smith Chart and Impedance Matching Tutorial with Examples20 Şubat 2020 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce)
- The Mizuhashi-Smith Chart3 Mart 2013 tarihinde Wayback Machine sitesinde arşivlendi. (İngilizce)
- 3D Smith chart tool2 Mayıs 2020 tarihinde Wayback Machine sitesinde arşivlendi. (Java gerektirir). Aktif ve pasif devre analizi programı