Sonlu elemanlar yöntemi

Sonlu elemanlar yöntemi ya da sonlu elemanlar metodu (FEM), mühendislik ve matematiksel modellerde sıklıkla kullanılan bir sayısal analiz yöntemidir. FEM, özellikle yapı statiği, ısı aktarımı, akışkanlar mekaniği, kütle aktarımı ve elektrik potansiyeli problemlerinde kullanılır; yöntem, özellikle iki veya üç boyutlu kısmi diferansiyel denklemleri ve sınır değer problemlerinin çözümünde uygulanır.[1]

u_{xx}+u_{yy}=-4

denklemin 1 yarıçaplı bir disk içinde çözümü. Çözümün gerçekleştirilebilmesi için alan küçük üçgenlere ayrılmıştır.

FEM, esasta geniş bir sistemi sonlu eleman adı verilen daha küçük bileşenlere ayırır: bu, denklemin çözüldüğü uzayın ayrıklaştırılarak küçük bölgelere bölünmesi ile gerçekleştirilir. Sınır değer probleminin bu formülasyonu sonucu bir cebirsel denklem sistemi elde edilir. bu sistem daha sonra Rayleigh–Ritz veya Galerkin metodu gibi değişkenli metodlar ile çözülür. Bu metodlarda sonuçlar temel fonksiyonlar (basis function) cinsinden elde edilir: diğer bir deyişle bu fonksiyonlar kullanılarak asıl çözümün interpolasyonu yapılır.[1][2]

Bir sistemin sonlu elemanlar yöntemi ile incelenmesi sonlu elemanlar analizi (FEA) olarak bilinmektedir. Yöntem ilk kez 1940'lı yıllarda öne sürülmüş ve 1950'li yıllarda uçak tasarımlarında kullanılmaya başlanmıştır.[2]

Sonlu elemanlar yöntemi ile modelleme örneği

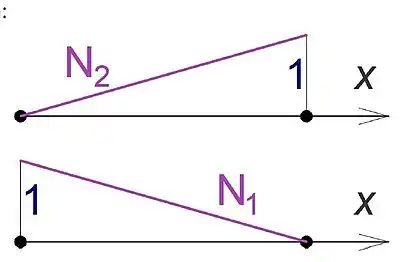
Bir yay modelinin sonlu elemanlar yöntemi ile incelenmesi aşağıdaki şekilde gerçekleştirilebilir:

1. Her bir yayı çeken 6kN kuvvetle uç uca bağlanmış iki yaydan oluşur. Yapının sol ucu "sabittir". Yayınların her birinin sertliği "21 kN / m" olarak verilmiştir.

2. Bu yapı, uygun bir şekilde 3 düğüme ve 2 öğeye ayrılabilir; öğe 1, düğüm 1 ve 2'ye ve öğe 2, düğüm 2 ve 3'e bağlanır. Düğümlerin yakınına yazılan sayılarla düğümleri tanımlamak gelenekseldir. Öğeler ayrıca sayılarla da belirtilir; eleman numaralarını düğüm numaralarından ayırmak için, bunlar genellikle daire içine alınır.

3. Bu yapıyı modellemek için, Şekil'de gösterildiği gibi 2 düğümlü tek boyutlu yay elemanlarını kullanmak en iyisidir. Bu nedenle eleman türü "doğrusal yay"dır. Bu unsur için aşağıdaki varsayımlar yapılmıştır: Yay, Hooke Yasasına uyar; yay yönünde kuvvetlere direnir. 1. ve 2. noktalar 'düğümlerdir'. f1 ve f2 yerel x yönündeki kuvvetlerdir. u1 ve u2 yerel düğüm yer değiştirmeleridir (düğüm serbestlik derecesi de denir). k- yay sabiti veya yayın sertliğidir. x, düğüm 1'den düğüm 2'ye giderken pozitif alınır.

4. Bu eleman için aşağıda verilen doğrusal bir yer değiştirme işlevi varsayılabilir: 𝑢=𝑎1 + 𝑎2𝑥. Matris biçiminde şu şekilde ifade edilebilir:

u=[1x]{\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}.

5. Katsayıları belirlemek için düğüm değerleri: 𝑢0 = 𝑢1 = 𝑎1, 𝑢𝐿 = 𝑢2 = 𝑎2𝐿 + 𝑢1,

a2={\frac {u2-u1}{L}}

. Bu nedenle, düğümsel terimlerle ifade edilen yer değiştirme işlevi şöyle olur:

u={\frac {u2-u1}{L}}x+u1

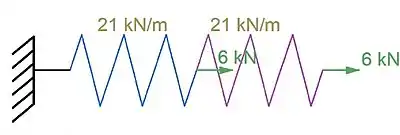
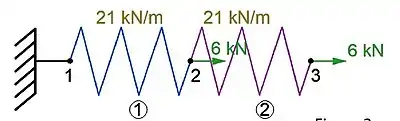
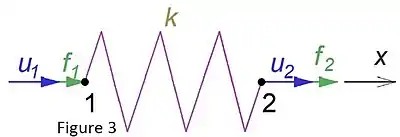
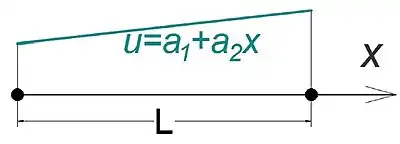
Galeri

2 boyutlu bir manyetik alan probleminin FEA için bölgelere ayrılması. Mavi renk ferromanyetik bir yapıyı ve kahverengi de iletken bir teli göstermektedir.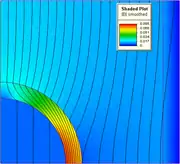
Manyetik alan probleminin FEA çözümü.
Bir köprünün FEA analiz animasyonu.

Ayrıca bakınız

Kaynakça

Zienkiewicz, Olek C.; Taylor, Robert L.; Zhu, J. Z. (2013). The finite element method: Its basis and fundamentals (İngilizce). Butterworth-Heinemann. ISBN 978-0-08-095135-5.
Jin, Jian-Ming (2014). The Finite element method in electromagnetics (İngilizce). Wiley-IEEE Press. ISBN 978-1-118-57136-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[ZienkiewiczTaylor2013-1] Zienkiewicz, Olek C.; Taylor, Robert L.; Zhu, J. Z. (2013). The finite element method: Its basis and fundamentals (İngilizce). Butterworth-Heinemann. ISBN 978-0-08-095135-5.

[jiangmin-2] Jin, Jian-Ming (2014). The Finite element method in electromagnetics (İngilizce). Wiley-IEEE Press. ISBN 978-1-118-57136-1.