Sayısal analiz
Sayısal analiz, diğer adıyla nümerik analiz veya sayısal çözümleme, matematiksel analiz problemlerinin yaklaşık çözümlerinde kullanılan algoritmaları inceler. Bu nedenle birçok mühendislik dalı ve doğa bilimlerinde önem arz eden sayısal analiz, bilimsel hesaplama bilimi olarak da kabul edilebilir. Bilgisayarın işlem kapasitesinin artması ile gündelik hayatta ortaya çıkan birçok sistemin matematiksel modellenmesi mümkün olmuş ve sayısal analiz algoritmaları burada ön plana çıkmıştır. 21. yüzyıldan itibaren bilimsel hesaplama yöntemleri mühendislik ve doğa bilimleri ile sınırlı kalmamış ve sosyal bilimler ile işletme gibi alanları da etkilemiştir. Sayısal analizin alt başlıklarına adi diferansiyel denklemlerin yaklaşık çözümleri ve özellikle veri biliminde önem taşıyan sayısal lineer cebir ile optimizasyon örnek gösterilebilir.[2][3][4]

Modern bilgisayarların icadından önce sayısal yöntemler kağıt üstünde uygulanıyordu. Her ne kadar 20. yüzyıl itibari ile ilgili hesaplamalar bilgisayarlar aracılığı ile yapılsa da, bu yazılımları oluşturan matematiksel algoritmaların temeli eski formüllere dayanmaktadır.[5]
Temeller
Direkt ve yinelemeli yöntemler
Direkt yöntemler sonucu tek bir adımda verirken, yinelemeli yöntemler sonuca birden fazla adım veya iterasyonda ulaşır. Özellikle doğrusal olmayan problemlerin hesaplanmasında yinelemeli yöntemlerin kullanılması gerekebilir;[6] buna karşın, matris faktörizasyonu ve lineer programlama gibi direkt sayısal yöntemler de mevcuttur.
Basit bir problemin direkt olarak cebir ve sayısal yineleme yöntemi ile çözümü şu şekilde karşılaştırılabilir:
x bilinmeyeninin olduğu
- 3x3 + 4 = 28
denklemini çözersek:
| 3x3 + 4 = 28. | |
| 4 çıkar | 3x3 = 24. |
| 3'e böl | x3 = 8. |
| Küp kökünü al | x = 2. |
Yineleme yöntemi olarak ikiye bölme metodu kullanılabilir; bu yöntemde fonksiyonun işaret değiştirdiği nokta tespit edilmeye çalışılır. Denklemi buna uygun olarak f(x) = 3x3 − 24 şeklinde yeniden yazabilir ve başlangıç değerleri olarak a = 0, b = 3, f(a) = −24 ve f(b) = 57 verebiliriz.
| a | b | mid | f(mid) |
|---|---|---|---|
| 0 | 3 | 1.5 | −13.875 |
| 1.5 | 3 | 2.25 | 10.17... |
| 1.5 | 2.25 | 1.875 | −4.22... |
| 1.875 | 2.25 | 2.0625 | 2.32... |
Tabloya göre sonuç 1.875 ile 2.0625 arasındadır. Algoritma bu aralık 0.2'den daha az bir hata ile herhangi bir sonucu verebilir.
Ayrıklaştırma
Ayrıklaştırma, bir fonksiyonun ya da operatörün ayrık değerlerle yaklaşık olarak hesaplanmasıdır. Örnek olarak, bir arabanın hızının yarım saatte bir ölçülmesiyle oluşturulan bir tablo ayrıklaştırılmış verileri gösterir; her ne kadar araba sürekli hareket etmiş olsa da veri tablosu ile zamana bağlı hızı gösteren ayrık bir fonksiyon elde edilebilir:
| Zaman | 0:20 | 0:40 | 1:00 | 1:20 | 1:40 |
|---|---|---|---|---|---|
| Hız (km/s) | 140 | 1:45 | 150 | 165 | 180 |
Fonksiyonların ayrıştırılmasına örnek olarak bir fonksiyonun türevi limit kullanarak şu şekilde yazılabilir:
Türevin yaklaşık olarak kullanılması gereken durumlarda limit yerine küçük ama sonlu bir değer alabilir ve bir x noktasındaki yaklaşık değer bu şekilde hesaplanabilir. Bu sayısal türev olarak ifade edilir. Aynı fonksiyonun x noktası için türevi Taylor serisi kullanılarak daha yakınsak bir şekilde de ifade edilebilir:[6]
Ayrıklaştırma, diferansiyel denklemlerin çözümünde ve sayısal integrallerde de sıklıkla kullanılmaktadır.
Yuvarlama, kesme ve ayrıklaştırma hataları
Yuvarlama hataları, sayısal hesaplamaların yapıldığı bilgisayarların sınırlı hafızalarının olmasından kaynaklanmaktadır: reel sayıların tüm hanelerini dijital veri şeklinde saklayabilmek mümkün değildir. Kesme hatası yinelemeli bir yöntemin sonlandırılması, ayrıklaştırma hataları ise sürekli bir sistem veya fonksiyonun ayrık bir şekilde yakınsanması ile ortaya çıkar. Sayısal yöntemleri yakınsama temelli olduğu için birçok durumda sonucun az da olsa kesin çözümden farklı olması beklenir; buna karşılık elde edilen sonucun hatası tolerans sınırları içinde olmalıdır. Özellikle matris problemleri için hata üst sınırı koşul sayısı (condition number) ile belirtilebilir.[6]
Nümerik stabilite
Bir algoritmanın nümerik açıdan stabil ya da kararlı olması, hatanın hesaplama sırasında çok büyümediğini ifade eder. Bu problemin "iyi koşullandırılmış" (well-conditioned) olmasını gerektirir. İyi koşullandırılma, verideki küçük bir değişikliğin sonuçta da küçük bir değişiklik yaratması olarak tanımlanabilir; bunun tersi "kötü koşullandırılmış" olarak tanımlanabilir.[7]
Alt dalları
Fonksiyonların değerlerinin sayısal olarak hesabı
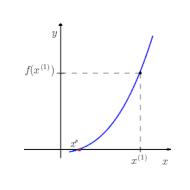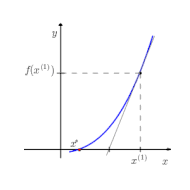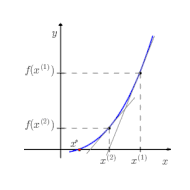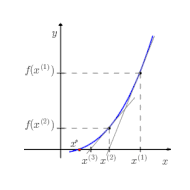
Fonksiyonların bir nokta için kesin hesabının etkili ya da mümkün olmadığı durumlarda Horner yöntemi gibi sayısal yöntemler kullanılabilir. Kök bulma algoritmaları için ise ikiye bölme metodu, Newton metodu, kiriş yöntemi ve Müller metodu örnek verilebilir.[8]
Doğrusal denklem sistemlerinin çözümleri
Özellikle doğrusal denklem sistemlerinin matris çözümlerinde sayısal yöntemler sıklıkla kullanılır; bunlardan bazılarına Gauss eleme yöntemi ve LU ile QR ayrışımları örnek gösterilebilir. Büyük boyutlu sistemlerde ise Jacobi metodu, Gauss-Seidel yöntemi veya konjuge gradyan metodu gibi yinelemeli çözümlemeler kullanılır. Doğrusal olmayan sistemler doğrusala yakınsabilir ve bu sistemler için Newton'un doğrusal olmayan sistem yöntemi kullanılabilir.[6]
Optimizasyon problemleri
Optimizasyon, bir fonksiyonun bazı sınırlamalar altındaki maksimum ya da minimum koşullarını sağlayan değerinin tespiti ile ilgilenir. Alt alanları arasında doğrusal programlama ve konveks optimizasyon örnek gösterilebilir.
İnterpolasyon, ekstrapolasyon ve regresyon

İnterpolasyon, bazı değerleri bilinen bir fonksiyonun ara değerlerinin tahmin edilerek doldurulması olarak tanımlanabilir. İnterpolasyon yöntemleri arasında noktaların doğrusal çizgiler ile birleştirilmesi (lineer interpolasyon) ve noktalara bir polinom fonksiyonun uyarlanması (polinom interpolasyonu) bulunmaktadır. Veri kümesi sınırları dışında bulunan bir noktadaki değerin tahmini ise ekstrapolasyondur.[6]
İstatistikte önem arz eden ve sayısal analiz sınırlarına da giren regresyon yöntemleri ise iki ya da daha çok değişken arasındaki ilişkiyi tahmin etmeye çalışır.[9] En basit regresyon tiplerinden biri olan doğrusal regresyonda veriye uyan bir doğrusal çizgi (fit) çekilir; bu en küçük kareler yöntemi ile yapılabilir.[6]
Özdeğer problemleri
Özellikle fizik ve mühendislik gibi alanlarda birçok problem özdeğer problemi olarak modellenebilir; bu durum sistemlerin özdeğerlerine ya da tekil değerlerine ayrıştırılmasını gerektirebilir. İstatistikte kullanılan temel bileşen analizi buna örnek gösterilebilir.[10]
Diferansiyel denklemlerin sayısal çözümü

Diferansiyel denklemlerin sayısal yöntemler ile çözümü bilimsel hesaplama için önem teşkil eden bir alt daldır. Özellikle birçok kısmi diferansiyel denklemlerin karmaşık geometrileri ve sınır koşulları için tam çözümü bulunamaz; bu nedenle denklemlerin ayrıklaştırılarak sınırlı bir alt uzayda çözülmesi gerekir.[11] Sonlu elemanlar,[12][13][14] sonlu farklar[15] ve sonlu hacim yöntemleri[16] ısı ve dalga denklemi gibi birçok denklemin karmaşık sistemlerde çözülmesinde ve simülasyonunda kullanılır. Adi diferansiyel denklemlerin çözümlerinde ise Runge-Kutta yöntemleri kullanılabilir.[6]
Sayısal integral hesabı
Belirli integrallerin yaklaşık olarak hesaplanması için kullanılan yöntemler arasında Yamuk kuralı formülü, Simpson (1/3) kuralı, Gauss dördünü ve Romberg yöntemi bulunmaktadır.[6]
Ayrıca bakınız
Kaynakça
- "Photograph, illustration, and description of the root(2) tablet from the Yale Babylonian Collection (İngilizce)". 13 Ağustos 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Temmuz 2020.
- Demmel, J. W. (1997). Applied numerical linear algebra. Society for Industrial and Applied Mathematics.
- Ciarlet, P. G., Miara, B., & Thomas, J. M. (1989). Introduction to numerical linear algebra and optimization. Cambridge University Press.
- Trefethen, Lloyd; Bau III, David (1997). Numerical Linear Algebra (1st ed.). Philadelphia: Society for Industrial and Applied Mathematics.
- Brezinski, C., & Wuytack, L. (2012). Numerical analysis: Historical developments in the 20th century. Elsevier.
- Ascher, Uri M.; Greif, Chen (2011). A First Course on Numerical Methods (5 bas.). Society for Industrial and Applied Mathematics. ISBN 9780898719970.
- Higham, N. J. (2002). Accuracy and stability of numerical algorithms (Vol. 80). SIAM.
- R. L. Burden, J. D. Faires, Numerical Analysis, 8th edition, Thomson Brooks/Cole, 2005. 0-534-39200-8
- Draper, N.R.; Smith, H. (1998). Applied Regression Analysis (3 bas.). John Wiley. ISBN 978-0-471-17082-2.
- Lever, Jake; Krzywinski, Martin; Altman, Naomi (2017). "Principal component analysis". Nature Methods (14): 641-642. doi:10.1038/nmeth.4346. 6 Nisan 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Temmuz 2020.
- Ames, W. F. (2014). Numerical methods for partial differential equations. Academic Press.
- Johnson, C. (2012). Numerical solution of partial differential equations by the finite element method. Courier Corporation.
- Brenner, S., & Scott, R. (2007). The mathematical theory of finite element methods. Springer Science & Business Media.
- Strang, G., & Fix, G. J. (1973). An analysis of the finite element method. Englewood Cliffs, NJ: Prentice-hall.
- Strikwerda, J. C. (2004). Finite difference schemes and partial differential equations. SIAM.
- LeVeque, Randall (2002), Finite Volume Methods for Hyperbolic Problems, Cambridge University Press.
Dış bağlantılar
- İTÜ Ninova Açık Ders Malzemeleri25 Eylül 2013 tarihinde Wayback Machine sitesinde arşivlendi., Sayısal yöntemler
- Massachusetts Teknoloji Enstitüsü ders notları11 Temmuz 2020 tarihinde Wayback Machine sitesinde arşivlendi., Sayısal yöntemlere giriş (İngilizce)