Altmışlık sayı sistemi

Altmış tabanı olarak da bilinen altmışlı,[1] altmışlık sistem veya altmışlık düzen, taban olarak altmış olan bir sayı sistemidir. MÖ 3. binyılda eski Sümerlerde ortaya çıktı, eski Babillilere aktarıldı ve günümüzde hala zamanı, açıları ve coğrafi koordinatları ölçmek için geçmişten bir miras olarak değiştirilmiş bir biçimde kullanılmaktadır.

Bir üstün yüksek derecede bileşik sayı olan 60 sayısı on iki çarpana sahiptir: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 ve 60, bunlardan 2, 3 ve 5 asal sayılardır. Bu kadar çok çarpanla, altmışlık sayıları içeren birçok kesir basitleştirilmiştir. Örneğin, bir saat eşit olarak 30 dakika, 20 dakika, 15 dakika, 12 dakika, 10 dakika, 6 dakika, 5 dakika, 4 dakika, 3 dakika, 2 dakika ve 1 dakikalık bölümlere bölünebilir. 60, 1'den 6'ya kadar her sayıya bölünebilen en küçük sayıdır; yani, 1, 2, 3, 4, 5 ve 6'nın en küçük ortak katı (EKOK)'dır.

Bu makalede, altmış tabanındaki rakamların tümü, aksi belirtilmediği sürece ondalık sayılarla temsil edilmektedir. Örneğin, 10, on sayısı ve 60, altmış sayısı anlamına gelir.

Kökeni

İnsanların yalnızca bir ellerini kullanarak parmaklarıyla 12'ye kadar saymaları mümkündür, baş parmak sırayla her bir parmak kemiğini işaret eder. Asya'nın birçok bölgesinde hala kullanımda olan geleneksel bir sayma sistemi bu şekilde çalışır ve 10, 20 ve 5'e dayalı olanların yanı sıra 12 ve 60'a dayanan sayı sistemlerinin oluşumunu açıklamaya yardımcı olabilir. Bu sistemde, bir el tekrar tekrar 12'ye kadar sayar, diğerinde yineleme sayısını gösterir, beş düzine, yani 60'a ulaşana kadar.[2][3]

Otto Neugebauer'e göre, altmış tabanının kökenleri, genellikle tasvir edildiği kadar basit, tutarlı veya zaman açısından tekil değildir. Bugün zaman, açılar ve astronomik koordinat sistemleri gibi özel konular için devam eden yüzyıllar süren kullanımları boyunca, altmışlık tabanda gösterimler, örneğin altmışlık sayıların nasıl yazıldığı gibi, her zaman güçlü bir ondalık notasyonu içermiştir. Bunların kullanımı, her zaman tek bir metinde bile sayıları temsil edecek çeşitli tabanların nerede ve nasıl temsil ettiği konusundaki tutarsızlıkları içermiştir (ve içermeye devam etmektedir).[4]

Erken Proto-çivi yazısı (MÖ 4. binyıl) ve alt-küçük sistem için çivi yazısı işaretleri (60, 600, 3600, vb.)

Altmışlık tabanın titiz ve tamamen kendi kendine tutarlı kullanımı için en güçlü itici güç, her zaman kesirleri yazmak ve hesaplamak için kullanılabilen matematiksel avantajları olmuştur. Eski metinlerde bu, altmışlık tabanın matematiksel veri tablolarında en düzgün ve tutarlı bir şekilde kullanıldığı gerçeğinde ortaya çıkar.[4] Geçmişte altmışlık tabanın kullanımını matematiksel tablolardan daha az tutarlı olsa da genişletmeye yardımcı olan bir başka pratik etken, tüccarlara ve alıcılara, daha büyük miktarlarda mal için pazarlık yapmak ve bunları bölmek söz konusu olduğunda günlük finansal işlemleri kolaylaştırmak için sağladığı avantajlardı. Erken shekel özelde bir mana’nın altmışta biriydi, daha sonra Yunanlılar bu ilişkiyi bir mina'nın ellide biri olan bir şekeli de 10 tabanına uyumlu oranda olmak zorunda bıraktılar.

Matematiksel tablolardan ayrı olarak, çoğu metinde sayıların temsil edilme şeklindeki tutarsızlıklar, sayısal büyüklükleri temsil etmek için kullanılan en temel çivi yazısı sembollerine kadar uzanmaktadır.[4] Örneğin, 1 için çivi yazısı sembolü, kamıştan yapılmış kalemin yuvarlak ucunun kile belirli bir açıyla uygulanmasıyla yapılmış bir elips iken, 60'ın altmış tabanında sembolü daha büyük bir oval veya "büyük 1" idi. Ancak bu sembollerin kullanıldığı aynı metinlerde 10 rakamı kalemin yuvarlak ucunun kile dik olarak uygulanmasıyla yapılmış bir daire olarak temsil edilmiş ve 100'ü temsil etmek için daha büyük bir daire veya "büyük 10" kullanılmıştır. Bu tür çok tabanlı sayısal miktar sembolleri, tek bir sayı içinde bile birbirleriyle ve kısaltmalarla karıştırılabilir. Belirtilen ayrıntılar ve hatta büyüklükler (sıfır tutarlı bir şekilde kullanılmadığından) belirli zaman dönemleri, kültürler ve temsil edilen miktarlar veya kavramlar için deyimseldi yani dilin özelliklerini taşıyordu. Sayısal büyüklüklerin bu tür bağlama bağlı temsillerinin geriye dönüp bakıldığında eleştirilmesi kolay olsa da, modern zamanlarda hala düzinelerce düzenli olarak kullanılan konuya bağlı taban karma örneğine sahibiz, bunlara ondalık kesirlerin altmış-tabanında astronomik koordinatlara eklenmesiyle ilgili son yenilikler de dahildir.

Kullanımı

Babil matematiği

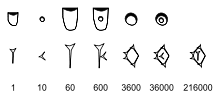
Eski Mezopotamya'da kullanıldığı şekliyle altmışlık sistem, basamakları için 60 farklı sembol kullanmadığı için saf bir taban 60 sistemi değildi. Bunun yerine, çivi yazısı rakamları, bir işaret-değer gösterimi tarzında bir alt taban olarak on'u kullandı: Altmışlık düzende basamaklar, dokuza kadar birimleri temsil eden bir grup dar, kama şeklindeki işaretten (, , , , ..., ) ve beş onluğa kadar temsil edilen geniş, kama şeklindeki işaretler grubundan (, , , , ) oluşuyordu. Bu işaretlerle yazılan rakamın değeri, bileşen parçalarının değerlerinin toplamıydı:

59'dan büyük sayılar, basamak değeri gösteriminde bu formun birden çok sembol bloğuyla gösterildi. Sıfır için sembol olmadığından, bir sayının nasıl yorumlanması gerektiği her zaman hemen açık değildir ve gerçek değeri bazen bağlamına göre belirlenmiş olmalıdır. Örneğin, 1 ve 60 için semboller aynıdır.[5][6] Daha sonra Babil metinlerinde sıfırı temsil etmek için bir yer tutucu () kullanıldı, ancak 13200 gibi sayılarda yaptığımız gibi sayının sağ tarafında değil, yalnızca yazılan sayının orta konumlarındaki rakam eksikliklerini gidermek için.[6]

Diğer tarihsel kullanımlar

Çin takviminde, günlerin veya yılların on kök dizisinde ve 12 daldan oluşan başka bir dizide konumlarla adlandırıldığı bir altmışlık döngü yaygın olarak kullanılır. Aynı gövde ve dal, bu döngü boyunca her 60 adımda bir tekrar eder.

Platon Devlet’inin VIII. Kitabı, 604 = 12960000 ve onun bölenleri üzerine odaklanan bir evlilik alegorisini içerir. Bu sayı, özellikle basit altmışlık temsili 1,0,0,0,0'a sahiptir. Daha sonraki bilim adamları, bu pasajı açıklamak için hem Babil matematiğini hem de müzik teorisini kullandılar.[7] [8]

Batlamyus'un Almagest adlı eseri, MS 2. yüzyılda matematiksel astronomi üzerine yazılmış bir inceleme, sayıların kesirli kısımlarını ifade etmek için 60 tabanını kullanır. Özellikle, bir milenyumdan (bin yıldan) fazla bir süredir esasen tek kapsamlı trigonometrik tablo olan kirişler tablosu, bir derecenin 60 tabanına göre kesirli kısımlarına sahiptir.

Ortaçağ gökbilimcileri, zamanı not etmek için altmış tabanına göre sayıları da kullandılar. El-Birûni, 1000'de Yahudi aylarını tartışırken, ilk olarak saati 60 tabanına benzer şekilde dakikalara, saniyelere, üçüncülere ve dördüncülere ayırdı.[9] 1235 civarında Sacroboscolu John bu geleneği sürdürdü, ancak Nothaft bunu yapan ilk kişinin Sacrobosco olduğunu düşündü.[10] Alfonsine tablolarının Paris versiyonu (yaklaşık 1320) günü temel zaman birimi olarak kullandı ve bir günün katlarını ve bölümlerini 60 tabana kaydederek gösterdi.[11]

Altmışlık sayı sistemi, 1671'e kadar Avrupalı gökbilimciler tarafından hesaplamalar yapmak için sıklıkla kullanılmaya devam etti.[12] Örneğin, Fundamentum Astronomiae’'deki Jost Bürgi (1592'de İmparator II. Rudolf'a sunulmuştur), Fundamentum Astronomicum’daki meslektaşı Ursus ve muhtemelen Henry Briggs, sinüsleri hesaplamak için 16. yüzyılın sonlarında seksagesimal (altmışlık) sisteme dayalı çarpım tablolarını kullandı.[13]

On sekizinci yüzyılın sonlarında ve on dokuzuncu yüzyılın başlarında Tamilli gökbilimcilerin, Helenistik gökbilimciler tarafından geliştirilen ondalık ve altmışlık gösterimlerin bir karışımını kullanıp kabuklarla hesaplamalar yaparak astronomik hesaplamalar yaptıkları bulundu.[14]

Taban-60 sayı sistemleri, Sümerlerle ilgisi olmayan diğer bazı kültürlerde, örneğin Batı Yeni Gine'deki Ekari halkı tarafından da kullanılmıştır.[15][16]

Modern kullanım

Altmışlık sistemin modern kullanımları arasında açıları ölçme, coğrafi koordinatlar, elektronik seyrüsefer ve zaman yer alır.[17]

Bir saat 60 dakikaya, bir dakika 60 saniyeye bölünür. Bu nedenle, 3:23:17 (3 saat, 23 dakika ve 17 saniye) gibi bir zaman ölçümü, tam altmışlık bir sayı (altmışlık taban noktası yok) olarak yorumlanabilir, yani 3 × 602 + 23 × 601 + 17 × 600 saniye. Ancak, bu sayıdaki üç altmışlık basamağın her biri (3, 23 ve 17) ondalık sistem kullanılarak yazılmıştır.

Benzer şekilde, pratik açısal ölçü birimi, bir daire içinde 360 (altı altmışlık) olan derecedir. Bir derecede 60 yay dakika ve dakikada 60 yay saniye vardır.

YAML

YAML veri depolama formatının 1.1[18] sürümünde, altmışlık sayılar düz skaler için desteklenir ve hem tam sayılar [19] hem de kayan nokta (float) sayıları resmi olarak destekler.[20] Bu, karışıklığa yol açmıştır, çünkü örneğin, bazı MAC adresleri altmışlık olarak algılanacak ve tam sayılar olarak yüklenecektir, diğerleri ise bu şekilde yüklenemeyecek ve dizge olarak yüklenecektir. YAML 1.2'de seksagesimale yönelik destek kaldırıldı.[21]

Gösterimler

Batlamyus'un yazıları gibi Helenistik Yunan astronomik metinlerinde, altmışlık sayılar Yunan alfabetik rakamları kullanılarak yazılırdı ve her altmışlık rakam ayrı bir sayı olarak değerlendirilirdi. Helenistik gökbilimciler sıfır için yeni bir sembol, —°, benimsedi; bu, yüzyıllar boyunca normalde 70 anlamına gelen Yunanca omikron (sembolü: ο) harfi de dahil olmak üzere diğer biçimlere dönüştü, buna ancak herhangi bir pozisyonda maksimum değerin 59 olduğu altmışlık sistemde izin verilebilir.[22][23] Yunanlılar altmışlık sayıları bir sayının kesirli kısmıyla sınırladılar.[24]

Ortaçağ Latince metinlerinde, altmışlık sayılar Arap rakamları kullanılarak yazılırdı; farklı kesir seviyeleri minuta (yani fraksiyon), minuta secunda, minuta tertia, vb. olarak belirtildi. On yedinci yüzyıla gelindiğinde, altmışlık sayıların tam sayı kısmını bir üst simge ile ve çeşitli kesirli bölümleri bir veya daha fazla vurgu işareti ile göstermek yaygın hale geldi. John Wallis, Mathesis universalis’inde bu gösterimi 60'ın yüksek katlarını içerecek şekilde genelleştirdi; örnek olarak 49‵‵‵‵36‵‵‵25‵‵15‵1°15′2″36‴49⁗ ; soldaki sayılar 60'ın daha yüksek üsleriyle çarpıldığında, sağdaki sayılar 60'ın katlarına bölünür ve üst simge sıfır ile işaretlenen sayı, 1 ile çarpılır.[25] Bu gösterim bizi, dereceler, dakikalar ve saniyeler için günümüzde kullandığımız modern işaretlere götürür. Aynı dakika ve saniye terminolojisi, zaman birimleri için de kullanılır ve saat, dakika ve saniyelerin ondalık olarak yazılan ve birbirinden iki nokta üst üste ile ayrıldığı modern zaman gösterimi, altmışlık bir gösterim biçimi olarak yorumlanabilir.

Bazı kullanım sistemlerinde, altmışlık noktadan sonra her pozisyon Latince veya Fransızca kökleri kullanılarak sayıldı: asal veya primus seconde veya secundus, tierce, quatre,, quinte vs. Bugüne kadar bir saatin ikinci dereceden kısmını veya bir dereceyi "saniye" olarak adlandırıyoruz. En azından 18. yüzyıla kadar, saniyenin 1/60'ı "tierce (kademe)" veya "third (üçüncü)" olarak adlandırıldı.[26][27]

1930'larda Otto Neugebauer, Babil ve Helenistik sayılar için, sayının tam ve kesirli kısımlarını ayırmak için noktalı virgül (;) kullanırken her bölüm içindeki konumları ayırmak için de virgül (,) kullanan, her pozisyonda 0'dan 59'a kadar modern ondalık gösterimi destekleyen modern bir gösterim sistemi geliştirdi.[28] Örneğin, hem Babil hem de Helenistik gökbilimciler tarafından kullanılan ve hala İbrani takviminde kullanılmakta olan ortalama sinodik ay 29; 31,50,8,20 gündür. Bu gösterim, bu makalede kullanılmaktadır.

Kesirler ve irrasyonel sayılar

Kesirler

Altmışlık sistemde, paydanın düzenli bir sayı (asal çarpanlarına ayırmada çarpanları sadece 2, 3 ve 5 olan) olduğu herhangi bir kesir tam olarak ifade edilebilir.[29] Burada, paydanın 60'tan küçük veya buna eşit olduğu bu türdeki tüm kesirler gösterilmektedir:

1⁄2 = 0;30
1⁄3 = 0;20
1⁄4 = 0;15
1⁄5 = 0;12
1⁄6 = 0;10
1⁄8 = 0;7,30
1⁄9 = 0;6,40
1⁄10 = 0;6
1⁄12 = 0;5
1⁄15 = 0;4
1⁄16 = 0;3,45
1⁄18 = 0;3,20
1⁄20 = 0;3
1⁄24 = 0;2,30
1⁄25 = 0;2,24
1⁄27 = 0;2,13,20
1⁄30 = 0;2
1⁄32 = 0;1,52,30
1⁄36 = 0;1,40
1⁄40 = 0;1,30
1⁄45 = 0;1,20
1⁄48 = 0;1,15
1⁄50 = 0;1,12
1⁄54 = 0;1,6,40
1⁄60 = 0;1

Ancak, düzenli olmayan sayılar daha karmaşık tekrarlayan kesirler oluşturur. Örneğin:

1⁄7 = 0;8,34,17 (çubuk altmışlık tabandaki rakamların dizisini gösterir 8,34,17 sonsuz sayıda defalarca tekrar eder)
1⁄11 = 0;5,27,16,21,49
1⁄13 = 0;4,36,55,23
1⁄14 = 0;4,17,8,34
1⁄17 = 0;3,31,45,52,56,28,14,7
1⁄19 = 0;3,9,28,25,15,47,22,6,18,56,50,31,34,44,12,37,53,41
1⁄59 = 0;1
1⁄61 = 0;0,59

Altmışa bitişik olan iki sayının, 59 ve 61'in her ikisinin de asal sayı olması gerçeği, bir veya iki altmışlık basamak periyoduyla tekrar eden kesirlerin paydalarının yalnızca düzgün sayı katları olan 59 veya 61 olabileceği anlamına gelir ve diğer düzgün olmayan sayıların daha uzun bir periyotta tekrar eden kesirleri vardır.

İrrasyonel sayılar
Yaklaşık olarak √2'ye eşit olan, altmışlık tabandaki 1;24,51,10 sayısını gösteren Babil tableti YBC 7289

Herhangi bir konumsal sayı sistemindeki irrasyonel sayıların temsili (ondalık ve altmışlık dahil) ne sona erer ne de tekrarlanır.

Bir birim karenin köşegeninin uzunluğu olan 2'nin karekökü, Eski Babil Dönemi (MÖ 1900 – MÖ 1650) Babilliler tarafından aşağıdaki şekilde ifade edilmiştir:

[30]

Çünkü √2 ≈ 1.41421356 ... bir irrasyonel sayıdır, tam olarak altmışlık (veya aslında herhangi bir tam sayı tabanındaki sistem) olarak ifade edilemez, ancak altmışlık tabandaki genişlemesi böyle başlar: 1; 24,51,10,7,46,6,4, 44. . . ( A070197)

Yunan matematikçi ve bilim adamı Batlamyus tarafından kullanılan π değeri 3;8,30 = 3 + 8/60 + 30/602 = 377/120 ≈ 3.141666.... idi.[31]

15. yüzyıldan Pers bir matematikçi olan Gıyaseddin Cemşid, 2π'yi dokuz alt rakama yuvarlandığında doğru değere sahip altmışlık tabanda bir ifade olarak hesapladı (dolayısıyla 1/608); 2π için değer 6; 16,59,28,1,34,51,46,14,50 idi.[32][33] Yukarıdaki √2 gibi, 2π de irrasyonel bir sayıdır ve tam olarak altmışlık düzende ifade edilemez. Altmışlık düzendeki açılımı 6; 16,59,28,1,34,51,46,14,49,55,12,35. . . şeklinde başlar. ( A091649)

Ayrıca bakınız

Kaynakça
  1. /sɛksəˈdʒɛsᵻməl/ ve /sɛkˈsædʒᵻnəri/ şeklinde telaffuz edilir; bakınız "sexagesimal." Oxford Dictionary of English 2e, Oxford University Press, 2003.
  2. Ifrah, Georges (2000), The Universal History of Numbers: From prehistory to the invention of the computer., New York: John Wiley and Sons, ISBN 978-0-471-37568-5, OCLC 42291138. Fransızca'dan David Bellos, E.F. Harding, Sophie Wood ve Ian Monk tarafından çevrilmiştir.
  3. Macey, Samuel L. (1989), written at Atlanta, Georgia, The Dynamics of Progress: Time, Method, and Measure, Atina, Londra: University of Georgia Press, s. 92, ISBN 978-0-8203-3796-8, OCLC 1113278749
  4. Neugebauer, Otto (1969), "The Exact Sciences In Antiquity", Acta Historica Scientiarum Naturalium et Medicinalium, New York: Dover, cilt 9, ss. 17-19, ISBN 978-0-486-22332-2, OCLC 13409, PMID 14884919
  5. Bello, Ignacio; Britton, Jack R.; Kaul, Anton (2009), Topics in Contemporary Mathematics (9. bas.), Avustralya, ABD: Cengage Learning, s. 182, ISBN 9780538737791, OCLC 326670156.
  6. Lamb, Evelyn (31 Ağustos 2014), "Ancient Babylonian Number System Had No Zero", Scientific American, Roots of Unity
  7. Barton, George A. (1908), "On the Babylonian origin of Plato's nuptial number", Journal of the American Oriental Society, cilt 29, ss. 210-219, doi:10.2307/592627, JSTOR 592627.
  8. McClain, Ernest G.; Plato (1974), "Musical "Marriages" in Plato's "Republic"", Journal of Music Theory, 18 (2), ss. 242-272, doi:10.2307/843638, JSTOR 843638
  9. Al-Biruni (1879) [1000], The Chronology of Ancient Nations, Sachau, C. Edward tarafından çevrildi, ss. 147-149
  10. Nothaft, C. Philipp E. (2018), written at Oxford, Scandalous Error: Calendar Reform and Calendrical Astronomy in Medieval Europe, Oxford, Birleşik Krallık: Oxford University Press, s. 126, ISBN 978-0-19-879955-9, OCLC 1022945273, Sacrobosco, altmışlık kesirlere geçti, ancak bunları güne değil saate uygulayarak takvimsel veya astronomik hesaplamada kullanıma daha uygun hale getirdi ve böylece 21. yüzyılda hala geçerli olan saat, dakika ve saniye kullanımını başlattı.
  11. Nothaft, C. Philipp E. (2018), written at Oxford, Scandalous Error: Calendar Reform and Calendrical Astronomy in Medieval Europe, Oxford, Birleşik Krallık: Oxford University Press, s. 196, ISBN 978-0-19-879955-9, OCLC 1022945273, Alfonsine Tablolarının Latin-Paris enkarnasyonlarında dikkate değer bir özelliği, tüm tablo haline getirilmiş parametrelerin katı şekilde 'altmış tabanına göre küçültülmesidir', çünkü hareketler ve zaman aralıkları tutarlı bir şekilde 60 taban katlarına ve günlerin veya derecelerin kesirlerine göre çözülmüştür.
  12. Newton, Isaac (1671), The Method of Fluxions and Infinite Series: With Its Application to the Geometry of Curve-lines., Londra: Henry Woodfall (1736 tarihinde yayınlandı), s. 146, Bunlardan en dikkat çekici olanı, Gökbilimciler arasında sıkça kullanılan Arithmetick'in Seksagesimal veya Altmışlık Ölçeği'dir; tüm olası Sayıları, Tam sayıları veya Kesirleri, Rasyonel veya Rasyonel olmayan, Altmışın kuvvetleri ve elli dokuzu aşmayan belirli sayı Katsayıları ile ifade eder.
  13. Folkerts, Menso; Launert, Dieter; Thom, Andreas (2016), "Jost Bürgi's method for calculating sines", Historia Mathematica, 43 (2), ss. 133-147, arXiv:1510.03180 $2, doi:10.1016/j.hm.2016.03.001, MR 3489006
  14. Neugebauer, Otto (1952), "Tamil Astronomy: A Study in the History of Astronomy in India", Osiris, cilt 10, ss. 252-276, doi:10.1086/368555; burada basılmıştır: Neugebauer, Otto (1983), Astronomy and History: Selected Essays, New York: Springer-Verlag, ISBN 0-387-90844-7
  15. Bowers, Nancy (1977), "Kapauku numeration: Reckoning, racism, scholarship, and Melanesian counting systems" (PDF), Journal of the Polynesian Society, 86 (1), ss. 105-116, 5 Mart 2009 tarihinde kaynağından (PDF) arşivlendi
  16. Lean, Glendon Angove (1992), Counting Systems of Papua New Guinea and Oceania, Ph.D. thesis, Papua New Guinea University of Technology, 5 Eylül 2007 tarihinde kaynağından arşivlendi. Özellikle bakınız; chapter 4 28 Eylül 2007 tarihinde Wayback Machine sitesinde arşivlendi..
  17. "Sexagesimal System", SpringerReference, Berlin/Heidelberg: Springer-Verlag, 2011, doi:10.1007/springerreference_78190
  18. "YAML Ain't Markup Language (YAML™) Version 1.1". 17 Ocak 2008 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Aralık 2020.
  19. "Integer Language-Independent Type for YAML™ Version 1.1". 9 Şubat 2005 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Aralık 2020.
  20. "Floating-Point Language-Independent Type for YAML™ Version 1.1". 9 Şubat 2005 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Aralık 2020.
  21. YAML Ain't Markup Language (YAML™) Version 1.2 (3rd Edition, Patched at 2009-10-01) §10.3.2 Tag Resolution, The Official YAML Web Site, 1 Ekim 2009, erişim tarihi: 30 Ocak 2019
  22. Neugebauer, Otto (1969) [1957], The Exact Sciences in Antiquity (2. bas.), Dover Publications, ss. 13-14, plate 2, ISBN 978-0-486-22332-2, PMID 14884919
  23. Mercier, Raymond, Consideration of the Greek symbol 'zero' (PDF), Home of Kairos
  24. Aaboe, Asger (1964), Episodes from the Early History of Mathematics, New Mathematical Library, 13, New York: Random House, ss. 103-104
  25. Cajori, Florian (2007) [1928], A History of Mathematical Notations, 1, New York: Cosimo, Inc., s. 216, ISBN 9781602066854
  26. Wade, Nicholas (1998), A natural history of vision, MIT Press, s. 193, ISBN 978-0-262-73129-4
  27. Lewis, Robert E. (1952), Middle English Dictionary, University of Michigan Press, s. 231, ISBN 978-0-472-01212-1
  28. Neugebauer, Otto; Sachs, Abraham Joseph; Götze, Albrecht (1945), Mathematical Cuneiform Texts, American Oriental Series, 29, New Haven: American Oriental Society and the American Schools of Oriental Research, s. 2
  29. Neugebauer, Otto E. (1955), Astronomical Cuneiform Texts, Londra: Lund Humphries
  30. Fowler, David; Robson, Eleanor (1998), "Square root approximations in old Babylonian mathematics: YBC 7289 in context", Historia Mathematica, 25 (4), ss. 366-378, doi:10.1006/hmat.1998.2209
  31. Toomer, G. J., (Ed.) (1984), Ptolemy's Almagest, New York: Springer Verlag, s. 302, ISBN 0-387-91220-7
  32. Youschkevitch, Adolf P., "Al-Kashi", Rosenfeld, Boris A. (Ed.), Dictionary of Scientific Biography, s. 256.
  33. Aaboe (1964), s. 125

İlave okumalar

Dış bağlantılar
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.