Asal sayı

Asal sayılar, sadece iki pozitif tam sayı böleni olan doğal sayılardır. Sadece kendisine ve 1 sayısına kalansız bölünebilen 1'den büyük pozitif tam sayılardır. ${\displaystyle \mathbb {P} }$ ile gösterilir. En küçük asal sayı 2'dir.[1]

Öklid'den beri asal sayıların sonsuz olduğu bilinir. Asal sayılar hakkındaki pek çok soru günümüzde hâlâ cevaplanamamaktadır.

Asırlardır asal sayılar üzerinde birçok teorem ortaya atılmış ve ispat edilmiştir. Asal sayıların bulunması için çeşitli formüller üretilmeye çalışılmış, fakat bunların hiçbiri bir sonuca varamamıştır. Sayılar Teorisi'nin en önemli uğraşısı asal sayılar hakkındaki bu tür sorulardır. Asal sayılar ayrıca kriptografi alanında yapı taşlarıdır.

1 sayısı

1 sayısı günümüzde ne asal ne de bileşik kabul edilir ve özel bir durumu vardır.[2] Geçmişte pek çok matematikçi 1'i asal sayı olarak kabul ediyordu. 1'in asal olarak kabul edilmesine dayanarak yapılan birçok çalışma geçerliliğini hâlâ sürdürmektedir: Stern ve Zeisel'in çalışmaları gibi. Henri Lebesgue, çalışmalarında 1'i asal olarak ele alan son profesyonel matematikçi olarak bilinir. 1 asal olarak ele alındığında bâzı teoremlerde değişikliğe gidilmesi gerekir. Örneğin tüm pozitif tam sayıların "yalnız bir şekilde" asal sayıların çarpımları şeklinde yazılabileceğini söyleyen aritmetiğin temel teoremi, geçmişteki asal sayı tanımına göre geçerli değildir.[3][4][5]

Resimdeki örnek 11'in asal olup 12'nin asal olmadığını gösteriyor.

Asal oturanlar

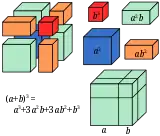
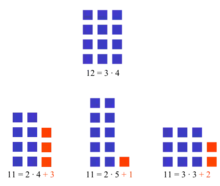
Aritmetiğin temel teoremi 1'den büyük tüm tam sayıların asal sayıların çarpımları şeklinde yazılabileceğini, üstelik yazımın da (asal çarpanların değişik sıralanması hariç) yalnız bir şekilde (teklik) olacağını söyler. Bir sayının asal çarpanlara ayrılmasında bir asal sayı birden fazla tekrar edebilir. Dolayısıyla asal sayılar, doğal sayıların "temel inşa taşları" olarak düşünülebilir.

Örneğin, 23244'ü şu şekilde asal çarpanlarına ayırabiliriz:
23244 = 2² × 3 × 13 × 149

ve 23244'ün diğer asal çarpanlara ayırış şekilleri yukarıdaki ile aynıdır, fakat asal sayıların sıralaması değişik olabilir. Büyük sayılar için değişik asal çarpanlara ayırma algoritmaları vardır.

İkiz asallar

Aralarındaki fark iki olan asal sayılar hakkındaki İkiz Asallar konjektürü.

Örneğin

• (3, 5)
• (5, 7)
• (11, 13)
• (17, 19)
• (29, 31)
• (41, 43)
• (59, 61)
• (71, 73)
• (101, 103)
• (107, 109)

Riemann hipotezi

Asal sayıların doğal sayılar içerisindeki dağılımı hakkındaki hipotezdir.

Goldbach hipotezi

Asal sayılarla ilgili Goldbach hipotezi, görünürde doğru gözükse de halen ispatlanamamıştır. "Her çift sayı iki asal sayının toplamı mıdır?"

Örneğin:

• 4 = 2 + 2
• 6 = 3 + 3
• 8 = 3 + 5
• 10 = 3 + 7
• 12 = 5 + 7
• 14 = 3 + 11
• 16 = 3 + 13
• 18 = 5 + 13
• 20 = 3 + 17
• 22 = 3 + 19
• 24 = 5 + 19
• 26 = 7 + 19
• 28 = 5 + 23
• 30 = 7 + 23
• 32 = 3 + 29
• 34 = 5 + 29
• 36 = 7 + 29

Mersenne sayıları

Asal bir a sayısı için (2^a – 1) biçiminde yazılan sayılara Mersenne sayıları denir.

Örneğin:

• 2 => 2² – 1 = 3
• 5 => 2⁵ – 1 = 31

Chen sayıları

A asal bir sayı olmak üzere (a+2) de asal bir sayı ise bu sayılara Chen sayıları denir.

Örneğin:

• 5 + 2 = 7
• 11 + 2 = 13

Ayrıca bakınız

• Asal sayıların listesi

Kaynakça

1. "Arşivlenmiş kopya". 12 Nisan 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Nisan 2020.
2. Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986. s 31.< 29 Mart 2013 tarihinde Wayback Machine sitesinde arşivlendi.>
3. Gowers, T (2002). Mathematics: A Very Short Introduction. Oxford University Press. ss. 118. ISBN 0-19-285361-9. The seemingly arbitrary exclusion of 1 from the definition of a prime … does not express some deep fact about numbers: it just happens to be a useful convention, adopted so there is only one way of factorizing any given number into primes
4. ""Why is the number one not prime?" 9 Mayıs 2008 tarihinde Wayback Machine sitesinde arşivlendi.". Retrieved 2007-10-02.
5. ""Arguments for and against the primality of 1 25 Ağustos 2007 tarihinde Wayback Machine sitesinde arşivlendi.".