Birleşme özelliği (küme teorisi)

Küme kuramında, birleşme, bir kümenin tüm ögelerinin topluluğudur ve ∪ ile sembolize edilir.

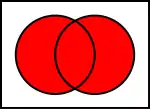
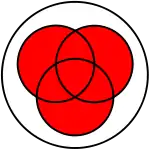
İki kümenin birleşimi:

~A\cup B

Üç kümenin birleşimi:

~A\cup B\cup C

İki kümenin birleşimi

A ve B kümelerinin birleşimi, A veya B deki veya hem A hem de B deki noktaların topluluğudur. İki kümenin birleşimi şöyle sembolize edilir;

A\cup B=\{x:x\in A\,\,\,{\textrm {or}}\,\,\,x\in B\}

.

Örneğin; A = {1, 3, 5, 7} ve B = {1, 2, 4, 6} ögelerinden oluşsun. Bu durumda A ∪ B = {1, 2, 3, 4, 5, 6, 7}. Daha açık örnek; A ve B sonsuz iki küme olsun:

A = {x, 1'den büyük çift tam sayı}

B = {x, 1'den büyük tek tam sayı}

A\cup B=\{2,3,4,5,6,\dots \}

Eğer "x" tek bir ögeden oluşan değişken ve A veya B kümesinde ya da her ikisinde bulunan bir öge olursa, bu durumda x, birleşme ögesi olur.

Kümelerde çoklu ögeler bulunmaz. Bu yüzden, {1, 2, 3} ile {2, 3, 4} kümesinin birleşimi {1, 2, 3, 4}'dür. Kümede veya içinde birden fazla eş (aynı nitelikli) öge bulunursa, öge sayısına sadece tek biri etki eder. 9 sayısı, {2, 3, 5, 7, 11, …} asal sayılar kümesi ile {2, 4, 6, 8, 10, …} çift sayılar kümesinin birleşimi değildir. Çünkü bu iki kümeden hiçbirinin ögesi değildir.

Cebirsel özellikler

İkili birleşme, bir birleşmeli işlemdir. Şöyle sembolize edilir:

A ∪ (B ∪ C) = (A ∪ B) ∪ C.

İşlemler herhangi bir sıraya göre gerçekleştirilebilir. Parantezler göz ardı edilebilir. Örneğin; yukarıdaki sembolik eşitlik aynı zamanda şöyle yazılabilir: A ∪ B ∪ C). Benzer şekilde birleşme, değişmelidir. Bu yüzden kümeler herhangi bir sıraya göre yazılabilir.

Boş küme, birleşme işleminde bir birim ögedir. Herhangi bir A kümesi için, A ∪ ∅ = A.

Sonlu birleşimler

Birkaç küme eşzamanlı olarak birleşebilir. Örneğin; A, B ve C kümelerinin birleşimi, A nın tüm ögeleri, B nin tüm ögeleri ve c nin tüm ögelerinden oluşur. Örneğin x, ancak ve ancak, A, B ve C kümelerinden en az birinin ögesi ise bu durumda, "x, A ∪ B ∪ C nin ögesidir" denir.

Matematikte sonlu birleşim, sonlu sayıdaki kümenin birleşimidir. Bu, birleşim kümesinin sonlu küme olacağı anlamına gelmez.

Ayrıca bakınız

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.