D'Alembert paradoksu

Akışkanlar dinamiğinde D’Alembert paradoksu veya hidrodinamik paradoks, 1752’de Fransız matematikçi Jean le Rond d'Alembert tarafından ortaya atılmıştır.[1] D’Alembert, matematiksel olarak sıkıştırılamaz ve akmazlığın olmadığı akışlarda kullanılan ve sanal fonksiyon teorisini baz alan potansiyel teorinin önemli bir açığını keşfetmiştir. Kaldırma kuvveti ile ilgili etkili sonuçlar veren potansiyel teori kullanıldığında, üzerinde akış olan her cisim için sürüklenme kuvveti sıfır oluyordu.[2]

Jean le Rond d'Alembert (1717-1783)

Bilim insanlarına göre bu çelişki, akmazlığın ihmalinden kaynaklanmaktadır. 19. ve 20. yüzyıllarda daha gelişmiş sistemlerle cisimler üzerindeki sınır tabakaları gözlendiğinde burada akmazlığın sınır koşulları nedeniyle çok etkili olduğu bulunmuştur. Sınır tabakası ince bile olsa, kuvvetler yüzeye uygulandığı için sürüklenme kuvvetleri çok büyüyebiliyordu. Ayrıca, uzun gövdeler için akışın ayrılarak arka bölgede basıncı çok düşük alanlar yaratması, dönüşler, türbülans gibi etkiler (tam olarak modellenemeyen etkiler) de burada güçlü olmaktadır.

Viskoz sürtünme; Saint-Venant, Navier ve Stokes

Bu paradoksu ilk çözmeye çalışan Saint Venant, akmazlıktan kaynaklanan sürtünmeyi modellemeye çalışmıştı.Moleküller arası basınç farkı ve yüzeydeki yapışmayı o zamanlardan tahmin edebilmişti.

1851’de Stokes, küre etrafındaki sürüklenme kuvvetini hesaplayabilmişti. Ancak bunu, düşük Reynolds sayıları için kendi kabulleriyle geliştirdiği Stokes yasası[3] olarak bilinen Stokes Akışı hesaplarıyla yapabilmekteydi. Ancak Navier’in katkılarına göre yetersizdi. Akış problemleri birimsiz formlara getirildiğinde, viskoz Navier-Stokes denklemleri artan Reynolds sayıları için Euler denklemlerinin potansiyel akış çözümlerine gelmektedir.[4] Bu durumda ise sürüklenme kuvveti yine sıfır olmalıdır, ancak ölçümler tam tersini göstermektedir.

Viskoz olmayan ayrılan akış: Kirchhoff ve Rayleigh
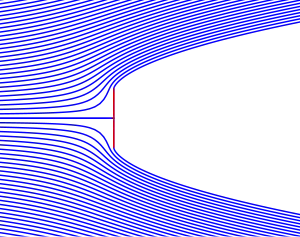
Akışa dik duran bir plaka üzerinden geçen, sıkıştırılamayan potansiyel akış (2 boyutta); kenarlardan ayrılan iki akış çizgisinin yol boyunca basınçları sabittir(ki bu da bu teorilerdeki hatayı getiriyor.)

19. yüzyılın ikinci yarısında, bilim insanları sürüklenme kuvvetini viskoz olmayan akış teorisi ile çözmeye çalışıyordu ve bunu viskozite etkisinin azaldığı yüksek Reynolds sayıları yapmaya çalışıyorlardı. Bu model Helmoltz’un serbest akış çizgileri metodunu baz alarak[5] Kirchhoff[6] ve Rayleigh[7] tarafından geliştirildi ve akışın gövde arkasında bir boşluk bıraktığı gözlemlendi-denendi. O zamanlar, arka bölgedeki kabuller, akış hızının gövde hızına hep eşit olduğu, ama sabit basınç olduğuydu. Yani arka bölgeye doğru karakteristik uzunluğun artmasıyla Reynolds sayısının fazlaca büyümesi, o dönemki bilim insanlarına potansiyel akış teorisini uygulayabileceklerini yani viskoz etkilerin minimum olduğu düşüncelerini vermekteydi. Bu çözüme göre, akış arkaya doğru geçtikçe düzgün bir şekilde gövdenin dışından ayrılmaktaydı ancak sürekli olmayan tanjant hız değişimleri sistem davranışına dahil oluyordu.[8][9] Gövde üzerinde sürüklenme kuvveti olması içinse, arka bölgenin sonsuza kadar uzanması gerekiyordu. Ancak bu teori, sürüklenme kuvvetinin hızın karesiyle doğru orantılı olduğunu söylüyordu.[10]

Ancak, o zamanlar vorteks ve akışın dönüşünden kaynaklanan stabil olmayan durumlardan ötürü akışın bu şekilde durgun olamayacağı biliniyordu. Bu tip düzensizliklere de genel olarak Kelvin-Helmholtz instabiliteleri[9] adı veriliyordu. Bu durgun akış modeli sürüklenme kuvvetini doğru vereceği düşünülerek oldukça çalışıldı.

Akışın gövdenin arka tarafına geçip kopmasından kaynaklanan sürüklenme kuvveti insanların kafasını bu çelişkilerle oldukça karışmıştı. Ve analitik olarak mevcut modellerle çözülemiyordu. Rayleigh[7] 1876’daki yayınında bu konunun hidrodinamiğin en kafa karıştırıcı alanı olduğunu ifade etmişti. Bu konudaki çözüme ilk önemli adım 1869’da Kirchhoff tarafından atıldı. Kirchhof, yukarıda bahsedildiği üzere, viskoz etkileri önemsemeden sadece arka bölgenin kopuşuna bağlı olarak sürüklenme kuvvetine yaklaşabileceği bir model geliştirdi(Günümüzde hala, bu yaklaşımı kullanabilir miyiz sorusu mevcuttur ve bilim insanları hidrodinamik dirence karşı Kirchhoff modelini kullanmaya çalışmaktadır.). Bunların üzerine Lord Kelvin “akışın ayrıldığı yüzeylerde hareket stabil değildir” yorumunu da eklemiştir. Kafaları daha da çok karıştıran bu ifadenin daha sonra viskoz etkilerden kaynaklandığı anlaşılacaktır. Ancak o dönemde insanlar küçük sınır tabakalarını gözlemleyemediği için onun etkilerini de bilmemekteydi veya önemsememekteydi. Buna bağlı olarak Rayleigh çok önemli bir yorum yaptı; “Direncin hesaplanırken materyalden direkt etkilenmesi mümkün olabilir. Çünkü basıncın gövdeden belli bir uzaklıkta, gövdede neler olduğundan etkilenmemesi gerekir. Dolayısıyla akışın instabilitesi gövdenin yakınında kendi kendini oluşturuyor olabilir.” [7] Bu önemli yorum, sınır tabaka teorisine giden yolu açarak fikirleri genişletti.

Kelvin eğer plakayı sabit hızda akışkan boyunca hareket ettirirse, arka bölgedeki hızın plakanın hızına eşit olduğunu gözlemledi. Dolayısıyla, teorinin instabiliteleri ve sürüklenme kuvvetlerinin gözlemlenebilmesi için gerektirdiği arka bölgenin sonsuza kadar genişletilmesi gerekliliği sonsuz kinetik enerjiye karşılık geldi ve bilim insanlarından tepki gördü.[10][11] Ayrıca, arka ve ön bölgede gözlemlenen basınç farkları ve bunlara bağlı hesaplanan bağlı hesaplanan sürüklenme kuvvetleri, gerçekte deneysel olarak bulunanlara göre çok daha az bulunuyordu. Örneğin, analitik hesaplamalar sürüklenme katsayısını 0.88 buluyorken gerçekte bu 2.0 olarak hesaplanıyordu. Dolayısıyla bu teori de sürüklenme kuvvetini açıklamak için yetersiz bulundu.[12]

İnce Sınır Tabaka Teorisi: Prandtl
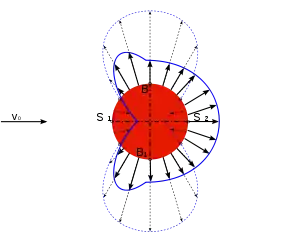
Silindir çevresindeki akışkan için basınç dağılımı. Kesikli mavi çizgi potansiyel akış teorisine göre basınç dağılımını gösteriyor. Düz mavi çizgi deneyler sonucu yüksek raynolds saylarında bulunan basınç dağılımını gösteriyor. Basınç silindirin yüzeyinden olan dairesel uzaklıktır. Pozitif basınç silindirin içinde, merkeze doğrudur. Negatif basınç silindirin dışına doğru çizilir.

Alman fizikçi Ludwig Prandtl 1904'te ince viskoz sınır tabakaların Rayleigh’in yorumundaki gibi sürüklenme kuvvetinde çok etkili olacağını ifade etti.[13] Prandtl bu fikri daha da ileri götürerek, yüksek hız ve Reynolds sayılarında kaymaz sınır koşulunun (akışkan parçacıklarının katı yüzeylerdeki düzensizliklere yapışması ve orada katıyla aynı hıza sahip olması) yakın bölgelerdeki serbest akış hızı ile gövdedeki akış hızı arasında ciddi farklara sebep olacağını ve bu ciddi farkların büyük kuvvetler yaratacağını da ifade etmişti. Ayrıca bu büyük kuvvetler, akışta momente dolayısıyla dönüşlere ve kaosa sebep olmaktaydı. Böylece akışın karışıp enerji alışverişi yapması ciddi oranda artmış oluyordu. Buradaki kinetik enerji alışverişi (daha genel bir ifadeyle sınırdaki akışkanların, dönüşten ötürü çevresine enerji saçması ve yüksek hız gradyanlarından ötürü karşı kuvvetlerle karşılaşması ile enerji kaybetmesi) diğer teorilerin tam olarak eksik kaldığı yeri doldurmaktaydı. Akış, yüksek kuvvet ve hareketlere karşı sanki katı bir tepeyi tırmanmaya çalışıyordu ve enerji kaybediyordu. Dolayısıyla serbest akış alanından aldığı enerjiyi bir süre sonra karşı kuvvetlere göre tamamen kaybediyor ve katıdan ayrılmaya başlıyordu. Bu ayrılma, arka bölgelere yani enerjinin en aza indiği yerlerde oluyor ve arka bölgelerde ciddi bir düşük basınç bölgesi bırakıyordu. Bu da yapısal sürüklenme kuvvetini (basınç farkından kaynaklanan) ortaya getiriyordu. Bu, sürtünmeden; viskoz etkilerden kaynaklanan sürüklenme kuvvetinden bile daha fazla olabiliyordu.

Prandtl’ın senaryosuna kanıt, uzun ve dik çıkan gövdelerde yüksek Reynolds sayılarındaki akışlarda bulunabilir. (Örneğin silindir) Başta, akış potansiyel teoriyle birebir uyumluluk gösterir ancak belli bir süre sonra enerjisi düştüğü için, durgunluk noktasında yani akışkan parçacıklarının dengeye geldiği yerde akışkan artık gövdeden ayrılır ve serbest akışa katılır; böylece arkada bir düşük basınç alanı kalır.[14]

Prandtl bu hipotezini, katıların yakınındaki ince tabakalarda viskoz etkilerin yüksek olması üzerine geliştirmiş ve bu bölgelere sınır tabaka adını vermiştir. Bu tabakalar katıdaki sıfır göreceli hızdan serbest akıştaki V hızına kadar olan gradyan bölgesinde oluşur ve buradaki yüksek gradyanlardan ötürü yüksek stresler oluşturur. Ancak bu bölgelerin haricinde viskoz etkiler; Newton’un akışkanlardaki kayma stresinin tanımına göre (hızın türevine bağlıdır) hız değişimleri çok az olduğu için kaybolur. Böylece sınır tabakaların dışında potansiyel teorinin doğru olduğu sonucuna varabiliriz. Viskoz etkilerin de işin içine dahil edildiği tam akışkan modeli (sürekli ortamlar mekaniği yani parçacıkların paketler halinde modellenmesi ile) doğrusal olmayan Navier-Stokes denklemleri ile tamamlanmıştır. Bu denklemler çoğu akış için matematiksel olarak hala çözülememektedir. Ancak Prandtl’ın hipotezi kullanılarak sınır tabakaların küçüklüğü ve içindeki olayların modellenmesi ile Navier-Stokes denklemleri çözülebilir formlara getirilebilmektedir. Düz bir plaka üzerindeki viskoz akış ise sınır tabaka modelinin Navier Stokes ile birlikte uygulanması ile Blasius (Prandtl’ın doktora öğrencisi) tarafından Rayleigh’in geliştirdiği boyutsuz sayılar uygulamasının da kullanılması ile(diferansiyel denklemlerin normalizasyonu kullanılmıştır) analitik olarak akış hakkındaki her bilgiyi bulabilmiştir. (Sürüklenme kuvveti, basınç değişimi, hız değişimi vb.) Prandtl teorisi hidrodinamik ve aerodinamik yapılar tasarlarken büyük önem kazanmıştır. Zira bu yapılarda, uzun ve çıkışlı gövdeler (bluff bodies) kullanılmaktadır ve bu gövdeler üzerindeki yapısal ve sürtünmeye dayalı sürüklenme kuvvetlerinin bulunması gerekmektedir.Ayrıca, tasarım bazında akış boyunca bütün basınç dağılımlarının bulunması bile büyük önem kazanmaktadır. Zira uçakların ve su altı araçlarının tasarımı sırasında basınç dağılımları, sürtünme kuvveti değişimleri; hangi parçaların ne şekilde tasarlanacağı hakkında önemli bilgiler vermektedir. Ayrıca, uçuş veya yüzme boyunca gövdenin hareketinin çevredeki akışkanı nasıl etkilediği bile önemli bir konudur.[15][16]

Notlar
  1. Jean le Rond d'Alembert (1752).
  2. Grimberg, Pauls & Frisch (2008).
  3. Stokes, G.G. (1851), "On the effect of the internal friction of fluids on the motion of pendulums", Trans. Camb. Philos. Soc., cilt 9, ss. 8-106, Bibcode:1851TCaPS...9....8S. Reprinted in Stokes, G.G., "On the effect...", Mathematical and Physical Papers, 2nd, Cambridge Univ. Press, 3
  4. The Stokes flow equations have a solution for the flow around a sphere, but not for the flow around a circular cylinder. This is due to the neglect of the convective acceleration in Stokes flow. Convective acceleration is dominating over viscous effects far from the cylinder (Batchelor, 2000, p. 245). A solution can be found when convective acceleration is taken into account, for instance using the Oseen equations (Batchelor, 2000, pp. 245–246).
  5. Helmholtz, H. L. F. von (1868), "Über discontinuierliche Flüssigkeitsbewegungen", Monatsberichte der Königlichen Akademie der Wissenschaften zu Berlin, cilt 23, ss. 215-228. Reprinted in: Philosophical Magazine (1868) 36:337–346.
  6. Kirchhoff, G. (1869), "Zur Theorie freier Flüssigkeitsstrahlen", Journal für die reine und angewandte Mathematik, cilt 70, ss. 289-298, doi:10.1515/crll.1869.70.289
  7. Rayleigh, Lord (1876), "On the resistance of fluids", Philosophical Magazine, 5 (2), ss. 430-441. Reprinted in: Scientific Papers 1:287–296.
  8. Batchelor (2000), pp. 338–339
  9. Wu, T. Y. (1972), "Cavity and wake flows", Annual Review of Fluid Mechanics, cilt 4, ss. 243-284, Bibcode:1972AnRFM...4..243W, doi:10.1146/annurev.fl.04.010172.001331
  10. Lamb, H. (1994), Hydrodynamics (İngilizce) (6th bas.), Cambridge University Press, s. 679, ISBN 978-0-521-45868-9
  11. Lord Kelvin (1894), "On the doctrine of discontinuity of fluid motion, in connection with the resistance against a solid moving through a fluid", Nature, 50 (1300), ss. 524-5, 549, 573-5, 597-8, Bibcode:1894Natur..50..524K, doi:10.1038/050524e0 Reprinted in: Mathematical and Physical Papers 4: 215–230.
  12. Batchelor (2000), p. 500.
  13. Prandtl (1904).
  14. Batchelor (2000), pp. 337–343 & plates.
  15. Schlichting, Hermann; Gersten, Klaus (2000), Boundary-layer theory (İngilizce) (8th revised and enlarged bas.), Springer, ISBN 978-3-540-66270-9, pp. XIX–XXIII.
  16. Batchelor (2000) pp. 302–314 & 331–337.

Kaynakça

Tarihsel

İleri Okuma
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.