Hızlı Fourier dönüşümü

Hızlı Fourier dönüşümü (Fast Fourier Transform–FFT) bir dizinin ayrık Fourier dönüşümünü (DFT) ya da ters ayrık dönüşümünü hesaplayan bir algoritmadır. Fourier analizinde bir sinyal bulunduğu uzaydaki (genellikle zaman uzayı) gösteriminden frekans uzayıki gösterimine ya da tersine dönüştürülür. DFT'de ise ayrık veri dizileri farklı frekans öğelerine ayrılır.[1] Bu operasyon her ne kadar birçok alanda kullanışlı olsa da, doğrudan formüllerle hesabı hızlı ve pratik değildir; bu nedenle DFT hesabı için FFT algoritmaları kullanılmaktadır.

İkiye bölmeli bir FFT örneği

Kosinüs dalgalarının toplamının ayrık Fourier analizi (10, 20, 30, 40 ve 50 Hz)

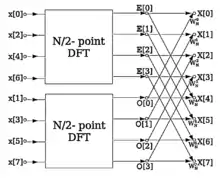
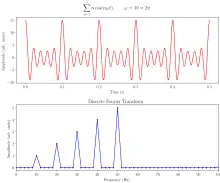
FFT algoritmaları DFT dönüşüm matrisinin seyrek matrislere ayrıştırılması ile çalışır.[2] Bu şekilde DFT'nin karmaşıklığı $O\left(N^{2}\right)$ 'den $O(N\log N)$ 'e düşürülebilmektedir; burada N veri boyutunu ifade eder. Veri boyutunun binler veya milyonlar mertebesinde olması durumunda FFT standart DFT'den çok daha hızlı çalışır. Yuvarlama hatası olması durumunda ise birçok FFT algoritmasının daha doğru sonuç verdiği belirtilebilir. Karmaşık sayı, grup teorisi ve sayılar teorisi temelli birçok farklı FFT algoritması bulunmaktadır. En yaygın FFT yöntemi Cooley–Tukey FFT algoritmasıdır.

FFT algoritmaları mühendislik, bilim, matematik ve müzikte sıklıkla kullanılmaktadır. Her ne kadar temelleri 1965'te popülerlik kazanmış olsa da, bazı temel yöntemlerinin geliştirilmesi 1805 yılına kadar dayanmaktadır.[1] Matematikçi Gilbert Strang, 1994 yılında FFT'yi "insan hayatındaki en önemli sayısal algoritmalardan biri" olarak tanımlamıştır.[3][4] IEEE'nin Computing in Science & Engineering dergisi ise FFT'ye "20. Yüzyılın En Önemli 10 Algoritması" listesinde yer vermiştir.[5]

Farklı programlama dillerinde FFT

Dil	Komut/Fonksiyon	Önkoşullar
R	stats::fft(x)	Yok
Octave/MATLAB	fft(x)	None
Python	fft.fft(x)	numpy
Mathematica	Fourier[x]	None
Julia	fft(A [,dims])	FFTW

Ayrıca bakınız

Kaynakça

Heideman, Michael T.; Johnson, Don H.; Burrus, Charles Sidney (1984). "Gauss and the history of the fast Fourier transform" (PDF). IEEE ASSP Magazine. 1 (4): 14-21. CiteSeerX 10.1.1.309.181 $2. doi:10.1109/MASSP.1984.1162257.
Van Loan, Charles (1992). Computational Frameworks for the Fast Fourier Transform. SIAM.
Strang, Gilbert (May–Haziran 1994). "Wavelets". American Scientist. 82 (3): 250-255. JSTOR 29775194.
Kent, Ray D.; Read, Charles (2002). Acoustic Analysis of Speech. ISBN 0-7693-0112-6.
Dongarra, Jack; Sullivan, Francis (Ocak 2000). "Guest Editors Introduction to the top 10 algorithms". Computing in Science & Engineering. 2 (1): 22-23. Bibcode:2000CSE.....2a..22D. doi:10.1109/MCISE.2000.814652. ISSN 1521-9615.

Dış bağlantılar

MIT FFT ders notları
Fast Fourier Transforms, bir online kitap (ed. Charles Sidney Burrus, 2008).
C++ dilinde Cooley–Tukey FFT algoritması
İnteraktif FFT

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Heideman_Johnson_Burrus_1984-1] Heideman, Michael T.; Johnson, Don H.; Burrus, Charles Sidney (1984). "Gauss and the history of the fast Fourier transform" (PDF). IEEE ASSP Magazine. 1 (4): 14-21. CiteSeerX 10.1.1.309.181 $2. doi:10.1109/MASSP.1984.1162257.

[Loan_1992-2] Van Loan, Charles (1992). Computational Frameworks for the Fast Fourier Transform. SIAM.

[Strang_1994-3] Strang, Gilbert (May–Haziran 1994). "Wavelets". American Scientist. 82 (3): 250-255. JSTOR 29775194.

[Kent_2002-4] Kent, Ray D.; Read, Charles (2002). Acoustic Analysis of Speech. ISBN 0-7693-0112-6.

[Dongarra_Sullivan_2000-5] Dongarra, Jack; Sullivan, Francis (Ocak 2000). "Guest Editors Introduction to the top 10 algorithms". Computing in Science & Engineering. 2 (1): 22-23. Bibcode:2000CSE.....2a..22D. doi:10.1109/MCISE.2000.814652. ISSN 1521-9615.