Hesaplamalı geometri

Hesaplamalı geometri, geometri açısından ifade edilebilen algoritmaların incelenmesine ayrılmış bilgisayar bilimlerinin bir dalıdır. Bazı çalışmalar tamamen geometrik problemlerden meydana gelirken bazıları ise hesaplamalı geometrik algoritmaların incelenmesinden sonucunda meydana gelmektedir.Bu gibi problemlerin hesaplama geometrisinin bir parçası olduğu düşünülmektedir.Modern hesaplamalı geometri son zamanlarda gelişme göstermesine karşın, tarihin antik dönemine kadar uzanan en eski bilgi işlem alanlarından biridir.

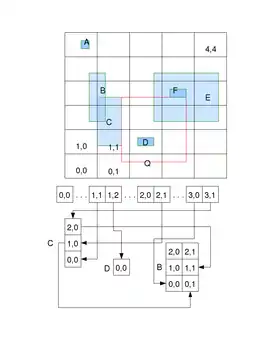
Hesaplama geometrisinde kullanılan ve verimli bölgelerin sorgulanmasına izin veren bir veri yapısı.

Hesaplama geometrisi ve hesaplama karmaşıklığı, algoritmalar onlarca veya yüz milyonlarca nokta içeren çok geniş veri kümelerinde kullanılıyorsa, pratik anlamda büyük önem taşır. Bu tür kümeler için, O (n2) ve O (n log n) arasındaki fark, hesaplamada gün ve saniye arasındaki fark gibi büyükçe olabilir.

Hesaplamalı geometrinin bir disiplin olarak geliştirilmesinin merkezinde bilgisayar grafikleri, bilgisayar destekli tasarım ve üretim(CAD / CAM) alanındaki ilerlemeler yer almaktaydı.Ancak hesaplama geometrisindeki birçok problem özünde klasik geometri problemleridir, matematiksel görselleştirme ve modelleme yoluyla bilgisayar bilimlerine dahil edilmiştir.

Hesaplama geometrisinin diğer önemli uygulamaları robotik (hareket planlama ve görünürlük problemleri), coğrafi bilgi sistemleri (CBS) (geometrik konum ve arama, rota planlama), entegre devre tasarımı (IC geometri tasarımı ve doğrulama), bilgisayar destekli mühendislik (CAE) (Mesh üretimi), bilgisayar görme (3 boyutlu yazıcı) gibi alanlardır.

Hesaplamalı geometride ana dallar şunlardır:

Kombinasyonel hesaplama geometrisi, algoritmik geometri olarak da adlandırılır ve geometrik nesneleri ayrı nesneler olarak ele alır. Bu konuda Preparata ve Shamos tarafından hazırlanan bir kitapta 1975 yılında "hesaplamalı geometri" teriminin ilk kullanımı tarihlenmektedir.[1]

Bilgisayar geometrisi, bilgisayar destekli geometrik tasarım (CAGD) veya geometrik modelleme olarak da adlandırılan ve CAD / CAM sistemlerinde bilgisayar hesaplamaları için uygun olan gerçek dünyadaki nesneleri temsil eden sayısal hesaplama geometrisi gibi alanları kapsamaktadır.Bütün bunlar hesaplamalı geometrinin büyük bir gelişimi olarak görülebilir ve bu alan genellikle bilgisayar grafiklerinin veya CAD'lerin bir dalı olarak düşünülür.

Kaynakça
  1. Franco P. Preparata and Michael Ian Shamos (1985). Computational Geometry - An Introduction. Springer-Verlag. 1st edition: ISBN 0-387-96131-3; 2nd printing, corrected and expanded, 1988: ISBN 3-540-96131-3.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.