Maxwell ilişkileri

Maxwell ilişkileri İkinci dereceden türevlerin simetri ve termodinamik potansiyellerin tanımlarından türetilebilen termodinamik denklemler dizisidir. Bu ilişkiler 19.yüzyıl fizikçisi James Clerk Maxwell tarafından adlandırılmıştır.

Maxwell ilişkileri arasındaki yolları gösteren akış şemasıdır. P: basınç, T: sıcaklık, V: hacim, S: entropi, α: termal genleşme katsayısı, κ: sıkıştırılabilme, C_V: sabit hacimdeki ısı kapasitesi , C_P: sabit basınçta ki ısı kapasitesi .

Eşitlikler

Maxwell ilişkilerinin yapısı, sürekli fonksiyonlar için ikinci türevler arasında olan eşitlik beyanıdır. Doğrudan iki değişkenin bir analitik işlev farklılaştırma sırasının alakasız olduğu (Schwarz teoremi) gerçeğinden yola çıkılmıştır. Maxwell ilişkileri söz konusu olduğunda, işlev termodinamik potansiyel x_i ve x_j potansiyeli için iki farklı doğal değişkenlerdir:

Schwarz' teoremi (genel) ${\displaystyle {\frac {\partial }{\partial x_{j}}}\left({\frac {\partial \Phi }{\partial x_{i}}}\right)={\frac {\partial }{\partial x_{i}}}\left({\frac {\partial \Phi }{\partial x_{j}}}\right)}$

Burada kısmi türevler, diğer tüm doğal değişkenler sabit tutulduğunda alınır. Her termodinamik potansiyel içinn(n − 1)/2 olası Maxwell ilişkisidir.Burada n o potansiyel için doğal değişkenlerin sayısıdır.

En yaygın dört Maxwell ilişkisi

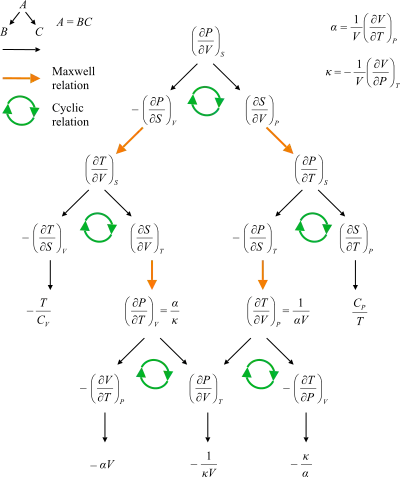
En yaygın olan dört Maxwell ilişkisi termal doğal değişkenine (sıcaklık T veya entropi S 'ye göre dört termodinamik potansiyelin her birinin ikinci türevlerinin eşitlikleridir ve mekanik doğal değişkenleridir (basınç' 'P' 'veya hacim' 'V' '):

Maxwell'in ilişkileri (bilinen adıyla) ${\displaystyle {\begin{aligned}+\left({\frac {\partial T}{\partial V}}\right)_{S}&=&-\left({\frac {\partial P}{\partial S}}\right)_{V}&=&{\frac {\partial ^{2}U}{\partial S\partial V}}\\+\left({\frac {\partial T}{\partial P}}\right)_{S}&=&+\left({\frac {\partial V}{\partial S}}\right)_{P}&=&{\frac {\partial ^{2}H}{\partial S\partial P}}\\+\left({\frac {\partial S}{\partial V}}\right)_{T}&=&+\left({\frac {\partial P}{\partial T}}\right)_{V}&=&-{\frac {\partial ^{2}F}{\partial T\partial V}}\\-\left({\frac {\partial S}{\partial P}}\right)_{T}&=&+\left({\frac {\partial V}{\partial T}}\right)_{P}&=&{\frac {\partial ^{2}G}{\partial T\partial P}}\end{aligned}}\,\!}$

Doğal termal ve mekanik değişkenlerinin fonksiyonları olarak potansiyellerin iç enerji U ( S, V ), entalpi H ( S, P , Helmholtz serbest enerjisi F ( T, V ) ve Gibbs serbest enerjisi G ( T, P ). Termodinamik kare bu ilişkileri türetmek için bir anımsatıcı olarak kullanılabilir. Bu ilişkilerin yararlılığı, sıcaklık, hacim ve basınç gibi ölçülebilir miktarlar açısından doğrudan ölçülebilen entropi değişikliklerini nicelikselleştirmeden kaynaklıdır.

Genel Maxwell ilişkileri

Yukarıdakiler sadece Maxwell ilişkileri değildir. Hacim çalışmalarının yanı sıra diğer doğal değişkenleri de içeren diğer çalışma koşulları düşünüldüğünde veya parçacıkların sayısı doğal bir değişken olarak dahil edildiğinde, diğer Maxwell ilişkileri belirginleşir. Örneğin, tek elementli bir gazımız varsa, partiküllerin sayısı N ise, aynı zamanda yukarıdaki dört termodinamik potansiyelin doğal bir değişkendir. Basınca ve partikül sayısına göre entalpi için Maxwell ilişkisi şöyledir:

${\displaystyle \left({\frac {\partial \mu }{\partial P}}\right)_{S,N}=\left({\frac {\partial V}{\partial N}}\right)_{S,P}\qquad ={\frac {\partial ^{2}H}{\partial P\partial N}}}$

Burada μ μ kimyasal potansiyeldir. Buna ek olarak, yaygın olarak kullanılan dört yanında başka termodinamik potansiyeller de vardır ve bu potansiyellerin her biri bir Maxwell ilişkileri seti verecektir.

Her denklem, ilişki kullanılarak yeniden ifade edilebilir

${\displaystyle \left({\frac {\partial y}{\partial x}}\right)_{z}=1\left/\left({\frac {\partial x}{\partial y}}\right)_{z}\right.}$

Bunlar bazen Maxwell ilişkileri olarak da bilinir.