Kenarortay

Kenarortay üçgende bir kenarın orta noktasını karşı köşeye birleştiren doğru parçası. Kenarortayların kesiştiği noktaya o üçgenin ağırlık merkezi denir ve G harfi ile adlandırılır.

Kenarortaylar ve ağırlık merkezi

Bir üçgende ağırlık merkezi kenarortayı ikiye bir oranında böler. Yani bir üçgende köşeye A, kenarortayın kenarı kestiği noktaya D dersek;
${\displaystyle |AG|=2|GD|}$

Kenarortay formülleri

Kenarortay uzunluğu

Bir üçgende kenarortayın uzunluğunu bulmak için;

${\displaystyle 2V_{a}^{2}=b^{2}+c^{2}-{\frac {a^{2}}{2}}}$ bağıntısı kullanılır.

Eğer tüm kenarortaylar için bu eşitlik yazılır ve taraf tarafa toplanırsa şu eşitlik elde edilir:

${\displaystyle 4(V_{a}^{2}+V_{b}^{2}+V_{c}^{2})=3(a^{2}+b^{2}+c^{2})}$

İspatı

Kenarortayın kenarı kestiği noktada bir açıya x, diğer açıya 180-x yazılırsa ve iki defa kosinüs teoremi uygulanıp taraf tarafa toplanırsa kenarortay teoremi elde edilir.

Dik üçgende kenarortay

Muhteşem üçlü

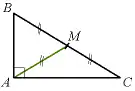
Bir dik üçgende A noktasından hipotenüse ait çizilen kenarortay doğru parçası hipotenüsün yarısına eşittir (Muhteşem üçlü):

${\displaystyle |MA|={\frac {|BC|}{2}}}$

Bir dik üçgende dik kenarlara ait kenarortaylarının karelerinin toplamı hipotenüse ait kenarortayın karesinin beş katıdır:

${\displaystyle V_{b}^{2}+V_{c}^{2}=5V_{a}^{2}={\frac {5}{4}}a^{2}}$

İspatı

Şu bağıntıyı yukarıda görmüstük:

${\displaystyle 4(V_{a}^{2}+V_{b}^{2}+V_{c}^{2})=3(a^{2}+b^{2}+c^{2})}$

Hipotenüs c kabul edilirse Pisagor teoremi gereği a²+b² yerine c² yazılır. Muhteşem üçlüye göre c yerine 2V_c yazılıp düzenlenirse eşitlik elde edilir.

Dik kesişen kenarortaylar

Eğer bir üçgende herhangi iki kenarortay dik olarak kesişiyorsa bu bağıntılar ortaya çıkar:

${\displaystyle V_{b}}$ ve ${\displaystyle V_{c}}$ dik kesişen kenarortaylar olmak üzere;

${\displaystyle V_{b}^{2}+V_{c}^{2}=V_{a}^{2}}$

Kenarortayın izdüşüm uzunluğu

Bir kenar üzerindeki yükseklik ile kenarortayı birleştiren doğru parçası kenarortayın izdüşümüdür ve uzunluğu(x) şu formülle hesaplanır:

${\displaystyle 2ax=|b^{2}-c^{2}|}$

Ayrıca bakınız

• Üçgen
• Açıortay