Geometrik dağılım

Olasılık kuramı ve istatistik bilim dallarında geometrik dağılım şu iki şekilde ifade edilebilen ayrık olasılık dağılımıdır:

• Bütün tam sayılar setine, yani { 1, 2, 3, .... } üzerine, bağlı olarak X sayıda Bernoulli denemesinde ilk başarıyı elde etmenin olasılık dağılımı; veya
• Bütün tam sayılar setine, yani {1, 2 ,3 , ....} üzerine, bağlı olarak ilk başarıyı elde etmeden Y = X − 1 başarısızlık sayısı olasılık dağılımı.

Geometrik

Olasılık kütle fonksiyonu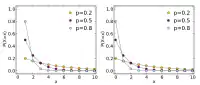
Yığmalı dağılım fonksiyonu
Parametreler	${\displaystyle 0<p\leq 1}$ başarı olasılığı (reel)
Destek	${\displaystyle k\in \{1,2,3,\dots \}\!}$
Olasılık kütle fonksiyonu (OYF)	${\displaystyle (1-p)^{k-1}\,p\!}$
Birikimli dağılım fonksiyonu (YDF)	${\displaystyle 1-(1-p)^{k}\!}$
Ortalama	${\displaystyle {\frac {1}{p}}\!}$
Medyan	${\displaystyle \left\lceil {\frac {-\log(2)}{\log(1-p)}}\right\rceil \!}$ (eğer ${\displaystyle -\log(2)/\log(1-p)}$ bir tam sayı ise tek değildir)
Mod	1
Varyans	${\displaystyle {\frac {1-p}{p^{2}}}\!}$
Çarpıklık	${\displaystyle {\frac {2-p}{\sqrt {1-p}}}\!}$
Fazladan basıklık	{{{basıklık}}}
Entropi	${\displaystyle -{\frac {1-p}{p}}\ln(1-p)-\ln p\!}$
Moment üreten fonksiyon (mf)	${\displaystyle {\frac {pe^{t}}{1-(1-p)e^{t}}}\!}$
Karakteristik fonksiyon	${\displaystyle {\frac {pe^{it}}{1-(1-p)\,e^{it}}}\!}$

İstatistikçiler aynı varsayımlara bağlı olarak geometrik dağılım için iki degişik şekilde açıklama ortaya çıkartmışlardır. Bunlar mantıken eşit olmakla beraber iki açıklamanın birbiri ile mutlak karıştırılmaması gerekir. Bunlardan ikinci açıklamaya kaydırılmış geometrik dağılımı adı verilmektedir. Bunlardan hangisinin geometrik dağılım olarak kabul edilip kullanılacağı elverişlilik ve matematiksel göreneklere göre değişir.

Birinci açıklamaya göre eğer her bir deneme için başarılılık olasılığı p ise, tek bir başarı elde etmek için gereken k deneme sayısı için olasılık şöyle verilir:

${\displaystyle \Pr(X=k)=(1-p)^{k-1}\,p\,}$

burada k = 1, 2, 3, ....

Eşit şekilde, kaydırılmış geometrik seri açıklamasına göre, eğer her bir deneme için başarılılık olasılığı p ise, ilk başarıyı elde etmeden k sayıda başarısızlık elde etme için olasılık şöyle verilir:

${\displaystyle \Pr(Y=k)=(1-p)^{k}\,p\,}$

burada k = 0, 1, 2, 3, ....

Dikkat edilirse burada iki değişik açıklama için değişik rassal değişken, X ve Y, kullanılmıştır. Her iki açıklamada da olasılık serileri bir geometrik seri olarak elde edilir.

Bir örnek olarak bir kusursuz zar atma deneyine bakılsın ve bir zar arka arkaya ilk defa 6 gelmesine kadar atılsın. İstenen bir sonucu elde etmek için gereken zar atılma sayısı için bir sonsuz sonuç seti (1, 2, 3, ... ) bulununur ve her bir deneme için yani her zar atışı için 6 gelmesi olasılığı p olur. Eğer 6 gelmeden önce atılması gereken zar sayısının olasılığı ilgi konusu ise bu birinci tip bir geometrik dağılımdır; eğer ilk 6 atmadan yapılan başarısız zar atması sayısı olasılığı ilgi konusu ise bu ikinci tip (kaydırılmış) geometrik dağılımdır.

Momentler ve kümülantlar

Geometrik dağılım gösteren X rassal değişkeni X için beklenen değer 1/p ve varyans değeri (1 − p)/p² :

${\displaystyle \mathrm {E} (X)={\frac {1}{p}},\qquad \mathrm {var} (X)={\frac {1-p}{p^{2}}}}$

olur.

Benzer şekilde, geometrik dağılım gösteren Y rassal değişkeni için beklenen değer ${\displaystyle (1-p)/p}$ ve varyans değeri ise ${\displaystyle (1-p)/p^{2}}$

${\displaystyle \mathrm {E} (Y)={\frac {1-p}{p}},\qquad \mathrm {var} (Y)={\frac {1-p}{p^{2}}}.}$

${\displaystyle \mu =(1-p)/p}$ değerinin Y için beklenen değer olduğu kabul edilsin. O zaman Y için olasılık dağılımının kümülant değeri ${\displaystyle \kappa _{n}}$ şu matematik yineleme ilişkisine (recursion) uyar:

${\displaystyle \kappa _{n+1}=\mu (\mu +1){\frac {d\kappa _{n}}{d\mu }}.}$

Parametre tahminleri

Geometrik dağılımın her iki alternatif şekli için p değerinin tahmini, dağılımın beklenen değerinin örnekleme ortalamasına eşit varsayımının kabulu suretiyle yapılabilir. Bu tahmin tipi istatistik kuramında tahmin için momentler yöntemi adı ile anılır. Geometrik dağılım için p değerinin bu yönteme göre tahmin edilmesi bir maksimum olabilirlilik tahmini ortaya çıkarır.

Özellikle geometrik dağılımın birinci alternatifi için ${\displaystyle i=1,\dots ,n}$ için ${\displaystyle k_{i}\geq 1}$ olduğu zaman

${\displaystyle k_{1},\dots ,k_{n}}$

bir örnekleme olduğu kabul edilsin. O zaman p değerinin tahmini şöyle verilir:

${\displaystyle {\widehat {p}}=\left({\frac {1}{n}}\sum _{i=1}^{n}k_{i}\right)^{-1}.\!}$

Bayes tipi sonuç çıkartıcı istatistik kuramına göre ise p parametresi için eşlenik önsel dağılımı bir Beta dağılımı olur. Eğer herhangi bir p parametre değeri için önsel olarak :Beta(α, β) verilmiş ise, sonsal dağılım şöyle ifade edilir:

${\displaystyle p\sim \mathrm {Beta} \left(\alpha +n,\ \beta +\sum _{i=1}^{n}(k_{i}-1)\right).\!}$

α ve β değerleri sıfıra yaklaştıkca, sonrasal ortalama olan ${\displaystyle \mathrm {E} [p]}$ maksimum olabilirlilik tahmini olan ${\displaystyle {\widehat {p}}}$ değerine yaklaşır.

Diğer alternatif halde, ${\displaystyle i=1,\dots ,n}$ için ${\displaystyle k_{i}\geq 0}$ olduğu halde bir örneklemin ifadesi ${\displaystyle k_{1},\dots ,k_{n}}$ olsun. Bu halde p şöyle tahmin edilir:

${\displaystyle {\widehat {p}}=\left(1+{\frac {1}{n}}\sum _{i=1}^{n}k_{i}\right)^{-1}.\!}$

Bir Beta(α, β) önseli için verilmiş p için sonsal dağılım şudur:

${\displaystyle p\sim \mathrm {Beta} \left(\alpha +n,\ \beta +\sum _{i=1}^{n}k_{i}\right).\!}$

Tekrar, sonsal ortalama olan ${\displaystyle \mathrm {E} [p]}$ değerinin, αve β sıfır değerine yaklaştıkca, maksimum olabilirlilik tahmini ${\displaystyle {\widehat {p}}}$ değerine yaklaşır.

Diğer özellikler

• X ve Y rassal değişkenleri için olasılık üreten fonksiyonlar sırasıyla şöyle ifade edilir:

${\displaystyle G_{X}(s)={\frac {s\,p}{1-s\,(1-p)}},\!}$

${\displaystyle G_{Y}(s)={\frac {p}{1-s\,(1-p)}},\quad |s|<(1-p)^{-1}.\!}$

• Geometrik dağılım, sürekli olasılık dağılım analogu olan üstel dağılım gibi, belleksiz olma özelliği gösterir. Bu demektir ki eğer bir deneyi ilk başarıyı elde edinceye kadar tekrarlarsak, birinci başarı daha ortaya çıkmadığı için, daha fazla sayıda yapılması gerek deneme sayısı için koşullu olasılık dağılımı o zamana kadar gözlemi yapılmış olan başarısızlık sayısına bağlı değildir. Deneme arka arkaya atılan zar veya havaya atılan ve tutulan madeni para ile yapılmakta ise, her deneme için önceki başarısızlıklar hakkında bilgi bulmak, sonuç bulmak için hiç yarar sağlamaz; yani deneme belleksizdir. Geometrik dağılım gerçekte tek belleksiz olan aralıklı olasılık dağılımıdır.
• Bütün tam sayılar seti, yani (1, 2, 3, ...), üzerinde desteklenen ve değeri verilmiş bir μ beklenen değeri bulunan, bütün aralıklı olasılık dağılımlar arasında, X rassal değişkeni için p = 1/μ parametreli geometrik dağılım en büyük entropi gösterenidir.
• İlk başarıdan önce başarısızlık sayısı olan Y rassal değeri için geometrik dağılım, sonsuz bölünebilirlilik özelliği gösterir. Bu demektir ki herhangi bir pozitif tam sayı olan n için, bağımsız ve birbiri ile aynı dağılım gösteren Y₁, ..., Y_n rassal değişkenleri vardır ve bunların toplamı Y ile aynı dağılım gösterir. Yalnızca n=1 hariç, bunlar geometrik dağılım göstermezler, bunların dağılımı negatif binom dağılımı ile temsil edilir.
• Geometrik dağılım gösteren bir Y rassal değişkeni için olasılık ondalıklı olarak yazılınca her on üssü için teksayı seri halinde bağımsızlık özelliği gösteren birer rassal değişken değeri olur. Örneğin, yüzlük sayı gösteren D teksayısı için bu rassal değişkenin olasılık dağılımı şöyle verilir:

${\displaystyle \Pr(D=d)={q^{100d} \over {1+q^{100}+q^{200}+\cdots +q^{900}}},}$

burada q = 1 − p. Diğer on üssü teksayıları için de benzer olasılık dağılımları ortaya çıkartılabilir.

Diğer dağılımlarla ilişkiler

• Y için geometrik dağılım r=1 olan özel bir negatif binom dağılımıdır. Daha genel olarak eğer 'Y₁,...,Y_r rassal değişkenleri için bağımsızlık gösteren p parametreli bir sıra geometrik dağılımlar görülüyorsa

${\displaystyle Z=\sum _{m=1}^{r}Y_{m}}$

r ve p parametreleri olan bir negatif binom dağılımı gösterir.

• Eğer Y₁,...,Y_r bir sıra bağımsız (olasılıkla değişik başarı parametreleri ${\displaystyle p^{(m)}}$) olan) geometrik dağılım gösteren değişkenlerse, bunların minimum değerlerini ifade eden

${\displaystyle W=\min _{m}Y_{m}\,}$

terimi de p parametresi

${\displaystyle 1-\prod _{m}(1-p^{(m)})}$

değerde olan bir geometrik dağılım gösterir.

• Eğer 0 < r < 1, ise ve bir rassal değişken olan k = 1, 2, 3, ... t i X_k beklenen değeri r^k/k olan bir Poisson dağılımı gösteriyorsa, o zaman

${\displaystyle \sum _{k=1}^{\infty }k\,X_{k}}$

(0, 1, 2, ....) setinden değerler alan ve beklenen değeri r/(1 − r) olan bir geometrik dağılım gösterir.

• Üstel dağılım geometrik dağılımın sürekli değişkenli analog benzeridir. Eğer bir üstel dağılım

gösteren rassal değişken değerleri tabandan yukarıya doğru, tavana en yakın tam sayıya yuvarlanırlarsa bu tam sayı halindeki rassal değişken de geometrik dağılım gösterir.

Ayrıca bakınız

• Kupon toplayıcısının problemi

Kaynakça

Dış bağlantılar

• Wolfram MathWorld Geometrik dağılım gösterimi 13 Eylül 2007 tarihinde Wayback Machine sitesinde arşivlendi. MathWorld (Erişim tarihi:12.8.2008